2023年陕西省西安市新城区爱知初级中学中考数学三模试卷（含答案）

这是一份2023年陕西省西安市新城区爱知初级中学中考数学三模试卷（含答案），共28页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2023年陕西省西安市新城区中考数学三模试卷
一、选择题（共10小题，每小题3分，计30分。每小题只有一个选项是符合题意的）
1．（3分）下列各数是无理数的是（　　）
A．2023 B． C． D．
2．（3分）如图所示的几何体的俯视图是（　　）

A． B． C． D．
3．（3分）如图，直尺经过一副三角尺中的一块三角板DCB的顶点B，若∠C＝30°，∠ABC＝20°，则∠DEF度数为（　　）

A．25° B．40° C．50° D．80°
4．（3分）正比例函数y＝kx（k≠0）的图象上有一点A到x轴的距离与到y轴的距离之比为，且y随x的增大而减小，则k的值为（　　）
A．﹣ B．﹣3 C． D．3
5．（3分）在下列计算中，正确的是（　　）
A．a3+2a3＝3a6 B．9a3b÷（﹣3a）2＝ab
C．a3b•2a2＝2a6b D．（﹣2a2b）3＝﹣6a3b3
6．（3分）如图，在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过点D作DE∥AC，交AB于E，若AB＝5，则线段DE的长为（　　）

A．2 B． C．3 D．
7．（3分）如图，在平面直角坐标系中，线段AB的端点坐标为A（1，1），B（3，2），一次函数y＝kx﹣2与线段AB有交点，则k的值不可能是（　　）

A． B． C．3 D．4
8．（3分）如图，在⊙O中，AC＝8，BD＝10，AB⊥CD于点E，若∠ABD＝30°，则⊙O的半径为（　　）

A． B．3 C． D．
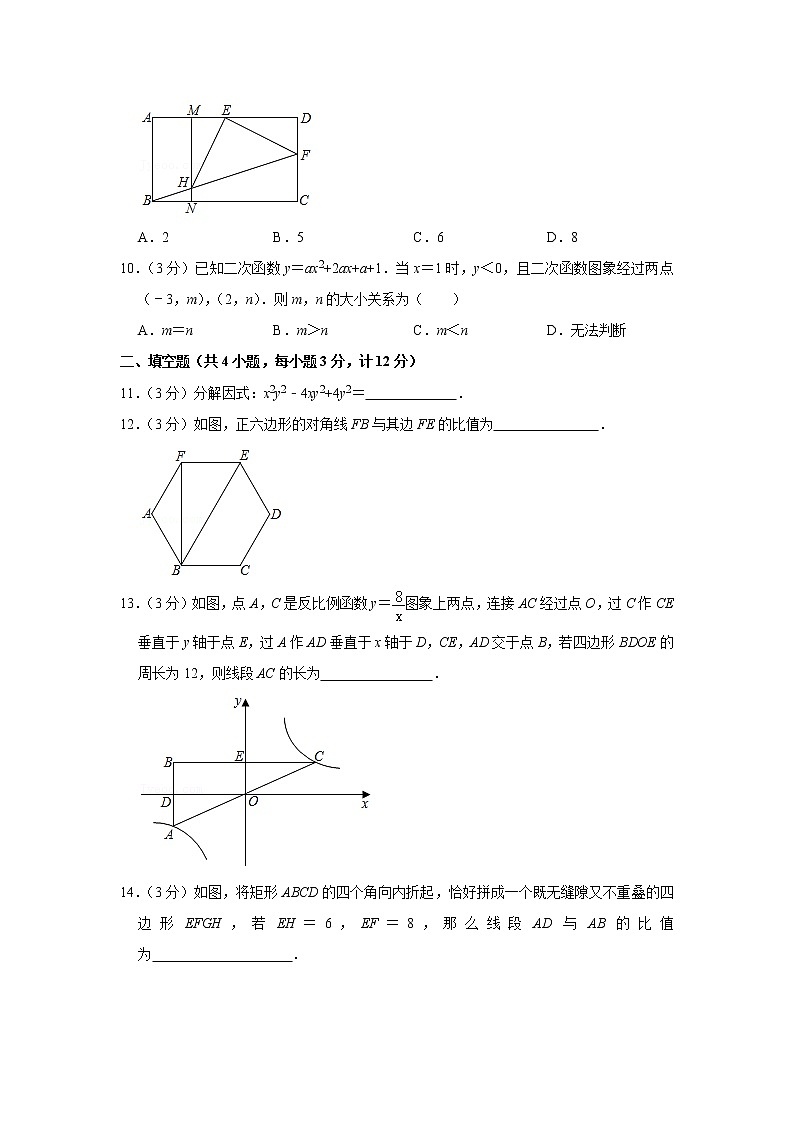
9．（3分）如图，在矩形ABCD中，BC＝12，点E为AD的中点，点F为CD边上一点，DF＝2，将线段EF绕点E顺时针旋转90°得到EH，点H恰好在线段BF上，过H作直线HM⊥AD于点M，交BC于点N，则CF的长为（　　）

A．2 B．5 C．6 D．8
10．（3分）已知二次函数y＝ax2+2ax+a+1．当x＝1时，y＜0，且二次函数图象经过两点（﹣3，m），（2，n）．则m，n的大小关系为（　　）
A．m＝n B．m＞n C．m＜n D．无法判断
二、填空题（共4小题，每小题3分，计12分）
11．（3分）分解因式：x2y2﹣4xy2+4y2＝　 　．
12．（3分）如图，正六边形的对角线FB与其边FE的比值为　 　．

13．（3分）如图，点A，C是反比例函数y＝图象上两点，连接AC经过点O，过C作CE垂直于y轴于点E，过A作AD垂直于x轴于D，CE，AD交于点B，若四边形BDOE的周长为12，则线段AC的长为　 　．

14．（3分）如图，将矩形ABCD的四个角向内折起，恰好拼成一个既无缝隙又不重叠的四边形EFGH，若EH＝6，EF＝8，那么线段AD与AB的比值为　 　．

三、解答题（共11小题，计78分．解答题应写出过程）
15．（5分）计算：2cos45°﹣|2﹣3|+（﹣）﹣1+（π﹣3.14）0．
16．（5分）化简：（x﹣1﹣）÷．
17．（5分）如图，已知点A是直线l外一点，点B是直线l上一点，请用尺规作⊙O，使得⊙O过点A且与直线l相切于点B．（要求：尺规保留作图痕迹，并把作图痕迹用黑色签字笔加黑）．

18．（5分）如图，正方形ABCD中，点G在对角线BD上（不与B、D重合），GE⊥DC于点E，GF⊥BC于点F，连接AG，CG．求证AG＝EF．

19．（7分）期末考试后，某市第一中学为了解本校九年级学生期末数学成绩情况，决定对该年级学生期末考试数学考试成绩进行抽样分析，已知九年级共有12个班，每班48名学生．请按要求回答下列问题：
收集数据：
（1）若要从全年级学生中抽取一个96人的样本，你认为以下抽样方法最合理的是　 　．（只填写序号）
①随机抽取两个班级的96名学生；
②在全年级学生中随机抽取96名学生；
③全年级12个班中分别各随机抽取8名学生；
④从全年级学生中随机抽取96名男生．
整理数据：
（2）将抽取的96名学生的成绩进行分组，绘制频数分布表和成绩分布扇形统计图（不完整）如下，根据图表中数据填空：
①A类成绩的频数为　 　，C类部分的圆心角度数为　 　；
②估计全年级A、B类学生大约一共有多少名？
成绩（单位：分）
频数
频率
A类（80～100）

0.5
B类（60～79）

0.25
C类（40～59）
16

D类（0～39）
8

分析数据：
（3）第一中学为了解学校教学情况，将第二中学九年级的抽样数据和本校进行对比，得表：
学校
平均分（分）
方差
中位数（分）
第一中学
73
432
80
第一中学
71
497
83
你认为哪所学校的教学效果较好？结合数据，请任选一个角度来解释你的观点．

20．（7分）小华去太华路小学参加中考体育测试时发现，太华路小学的路灯照明是依靠太阳能光板供给的，如图所示，路灯立柱AB长10.3米，支架CO的长为0.4米，支点C到立柱顶端B的距离为0.3米，支架OC与立柱AB的夹角∠OCA＝120°，支架OC与光板DE垂直，太阳能光板DE长为1.2米，点O是DE的中点，求太阳能光板最低点E离地面的高度（结果保留根号），

21．（7分）甲、乙两人用扑克牌玩“10点”游戏，游戏规则如下：
①将牌面数字作为点数，如红桃6的点数就是6（牌面点数与牌的花色无关）；
②每人摸2次，每次摸一张（不放回），将所摸的两张牌的点数相加，若点数之和小于或等于10，此时点数就是最终点数；若点数之和大于10，则最终点数是0；
③游戏结束前双方均不知道对方点数；
④判定游戏结果的依据是：最终点数大的一方获胜，最终点数相等时不分胜负．现在甲已经摸出了两张牌，且这两张牌的数字之和是8，这时桌上还有四张背面朝上的扑克牌，牌面数字分别是4、5、6、7，如图所示．
（1）若乙从桌面上随机摸出一张扑克牌，点数为6的概率是多少？
（2）根据题意和游戏规则，甲乙双方谁获胜的可能大？
22．（7分）每年5月，西安郊区的樱桃大量成熟，某樱桃种植户对樱桃的销售价格规定如下：一次购买2千克以下（含2千克）樱桃，单价为a元/千克；一次购买2千克以上，超过2千克部分的樱桃价格打七五折，小华对购买量x（千克）和付款金额y（元）这两个变量的对应关系做了分析，绘制了如图所示的函数图象．请你根据图象回答下列问题．
（1）求y与x的函数关系式：
（2）已知小华将30元钱全部用于购买樱桃，小丽购买了2千克樱桃，如果他们两个人合起来购买，可以比分开购买多买多少千克樱桃？

23．（8分）如图，四边形ABCD内接于⊙O，BD是⊙O的直径，过点A作⊙O的切线交CD的延长线于点E，DA平分∠BDE．
（1）求证：AE⊥CD．
（2）若AB＝4，AE＝2，求CD的长．

24．（10分）已知抛物线L1过点A（﹣1，0）、B（3，0）、C（0，﹣3）．
（1）求该抛物线的表达式．
（2）抛物线L1的对称轴与x轴交于点P，将该抛物线沿直线y＝m翻折得抛物线L2，在抛物线L2第四象限的图象上是否存在一点D，使的△CPD是以CP为直角边的等腰直角三角形？若存在，求出满足条件的L2的解析式；若不能，请说明理由．

25．（12分）圆的定义：在同一平面内，到定点的距离等于定长的所有点所组成的图形．
（1）已知：如图1，OA＝OB＝OC，请利用圆规画出过A、B．C三点的圆．若∠AOB＝70°，则∠ACB＝　 　．
如图，Rt△ABC中，∠ABC＝90°，∠BCA＝30°，AB＝2．
（2）已知，如图2．点P为AC边的中点，将AC沿BA方向平移2个单位长度，点A、P、C的对应点分别为点D、E、F，求四边形BDFC的面积和∠BEA的大小．
（3）如图3，将AC边沿BC方向平移a个单位至DF，是否存在这样的a，使得直线DF上有一点Q，满足∠BQA＝45°且此时四边形BADF的面积最大？若存在，求出四边形BADF面积的最大值及平移距离a，若不存在，说明理由．


2023年陕西省西安市新城区爱知中学中考数学三模试卷
参考答案与试题解析
一、选择题（共10小题，每小题3分，计30分。每小题只有一个选项是符合题意的）
1．（3分）下列各数是无理数的是（　　）
A．2023 B． C． D．
【解答】解：A、2023是整数，属于有理数，故本选项不合题意；
B、是分数，属于有理数，故本选项不合题意；
C、，属于无理数，故本选项符合题意；
D、，是整数，属于有理数，故本选项不合题意．
故选：C．
2．（3分）如图所示的几何体的俯视图是（　　）

A． B． C． D．
【解答】解：从上往下看，得两个长方形的组合体．
故选：D．
3．（3分）如图，直尺经过一副三角尺中的一块三角板DCB的顶点B，若∠C＝30°，∠ABC＝20°，则∠DEF度数为（　　）

A．25° B．40° C．50° D．80°
【解答】解：∵∠C＝30°，∠ABC＝20°，
∴∠BAD＝∠C+∠ABC＝50°，
∵EF∥AB，
∴∠DEF＝∠BAD＝50°，
故选：C．
4．（3分）正比例函数y＝kx（k≠0）的图象上有一点A到x轴的距离与到y轴的距离之比为，且y随x的增大而减小，则k的值为（　　）
A．﹣ B．﹣3 C． D．3
【解答】解：∵函数y＝kx图象上的点y随x的增大而减小，
∴k＜0，
∵函数y＝kx图象上点A到x轴的距离与到y轴的距离之比为，
∴|k|＝||＝，即k＝﹣，
故选：A．
5．（3分）在下列计算中，正确的是（　　）
A．a3+2a3＝3a6 B．9a3b÷（﹣3a）2＝ab
C．a3b•2a2＝2a6b D．（﹣2a2b）3＝﹣6a3b3
【解答】解：A、原式＝3a3，不符合题意；
B、原式＝9a3b÷9a2＝ab，符合题意；
C、原式＝2a5b，不符合题意；
D、原式＝﹣8a6b3，不符合题意．
故选：B．
6．（3分）如图，在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过点D作DE∥AC，交AB于E，若AB＝5，则线段DE的长为（　　）

A．2 B． C．3 D．
【解答】解：∵AD平分∠BAC，
∴∠BAD＝∠CAD，
∵DE∥AC，
∴∠CAD＝∠ADE，
∴∠BAD＝∠ADE，
∴AE＝DE，
∵AD⊥DB，
∴∠ADB＝90°，
∴∠EAD+∠ABD＝90°，∠ADE+∠BDE＝∠ADB＝90°，
∴∠ABD＝∠BDE，
∴DE＝BE，
∵AB＝5，
∴DE＝BE＝AE＝AB＝2.5，
故选：B．
7．（3分）如图，在平面直角坐标系中，线段AB的端点坐标为A（1，1），B（3，2），一次函数y＝kx﹣2与线段AB有交点，则k的值不可能是（　　）

A． B． C．3 D．4
【解答】解：把A（1，1）代入y＝kx﹣2得，1＝k﹣2，解得k＝3，
把B（3，2）代入y＝kx﹣2得，2＝3k﹣2，解得k＝，
若直线y＝kx﹣2与线段AB有交点，则≤k≤3，
所以k的值不可能是4．
故选：D．
8．（3分）如图，在⊙O中，AC＝8，BD＝10，AB⊥CD于点E，若∠ABD＝30°，则⊙O的半径为（　　）

A． B．3 C． D．
【解答】解：如图，过点O作OM⊥AB于M，ON⊥CD于N，连接OD．

∵AB⊥CD，
∴∠OME＝∠ONE＝∠MEN＝90°，
∴四边形OMEN是矩形，
∴OM＝EN，ON＝EM，
在Rt△ACE中，∵BD＝6，∠B＝∠ACD＝30°，
∴DE＝BD＝5，AE＝5，
在Rt△AEC中，∵BD＝6，∠ACE＝30°，
∴AE＝AC＝4，EC＝4，
∴CD＝5+4，AB＝4+5，
∵OM⊥AB，ON⊥CD，
∴AM＝BM＝，CN＝DN＝，
∴EM＝ON＝，
∴OD＝＝＝．
故选：A．
9．（3分）如图，在矩形ABCD中，BC＝12，点E为AD的中点，点F为CD边上一点，DF＝2，将线段EF绕点E顺时针旋转90°得到EH，点H恰好在线段BF上，过H作直线HM⊥AD于点M，交BC于点N，则CF的长为（　　）

A．2 B．5 C．6 D．8
【解答】解：过H点作MN⊥AD，则MN∥CD，设CF＝x．
∵AB＝CD＝DF+CF＝2+x，BC＝12，E为边AD的中点，
∴AE＝ED＝6，
∵∠FEH＝90°，
∴∠MEH+∠DEF＝90°，
∵∠DEF+∠DFE＝90°，
∴∠MEH＝∠DFE，
在△MEH和△DFE中，
，
∴△MEH≌△DFE（AAS），
∴ME＝DF＝2，MH＝DE＝6，
∴HN＝x+2﹣6＝x﹣4，
∴BN＝AM＝6﹣2＝4，
∵NH∥CF，
∴△BNH∽△BCF，
∴＝，即＝，
解得x＝6，
∴CF的长是6，
故选：C．

10．（3分）已知二次函数y＝ax2+2ax+a+1．当x＝1时，y＜0，且二次函数图象经过两点（﹣3，m），（2，n）．则m，n的大小关系为（　　）
A．m＝n B．m＞n C．m＜n D．无法判断
【解答】解：∵二次函数y＝ax2+2ax+a+1，
∴对称轴为直线x＝﹣＝﹣1，
∵当x＝1时，y＜0，
∴a+2a+a+1＜0，
∴a＜﹣，
∴抛物线开口向下，
而点（﹣3，m）到直线的距离小于点（2，n）到直线x＝﹣1的距离小，
∴m＞n．
故选：B．
二、填空题（共4小题，每小题3分，计12分）
11．（3分）分解因式：x2y2﹣4xy2+4y2＝　y2（x﹣2）2　．
【解答】解：原式＝y2（x2﹣4x+4）
＝y2（x﹣2）2．
故答案为：y2（x﹣2）2．
12．（3分）如图，正六边形的对角线FB与其边FE的比值为　　．

【解答】解：∵六边形ABCDEF是正六边形，
∴AB＝AF＝EF，∠BAF＝∠AFE＝∠ABC＝（6﹣2）×180°＝120°，∠ABE＝∠ABC＝60°，
∴∠AFB＝∠ABF＝（180°﹣120°）＝30°，
∴∠BFE＝120°﹣30°＝90°，∠EBF＝60°﹣30°＝30°，
∴FB＝FE，
∴＝，
故答案为：．
13．（3分）如图，点A，C是反比例函数y＝图象上两点，连接AC经过点O，过C作CE垂直于y轴于点E，过A作AD垂直于x轴于D，CE，AD交于点B，若四边形BDOE的周长为12，则线段AC的长为　4　．

【解答】解：设C（m，n），则A（﹣m，﹣n），
∴OD＝m，BD＝n，
∵四边形BDOE的周长为12，
∴2（m+n）＝12，
∴m+n＝6，
∵点A，C是反比例函数y＝图象上两点，
∵mn＝8，
∴m＝4，n＝2，
∴A（﹣4，﹣2），C（4，2），
∴AC＝＝4，
故答案为4．
14．（3分）如图，将矩形ABCD的四个角向内折起，恰好拼成一个既无缝隙又不重叠的四边形EFGH，若EH＝6，EF＝8，那么线段AD与AB的比值为　　．

【解答】解：∵∠HEM＝∠AEH，∠BEF＝∠FEM，
∴∠HEF＝∠HEM+∠FEM＝×180°＝90°，
同理可得：∠EHG＝∠HGF＝∠EFG＝90°，
∴四边形EFGH为矩形，
∵∠B＝∠D，∠BEF＝∠DGH，EF＝GH，
∴△BEF≌△DGH（AAS），
∴BF＝DH，
∵FM＝BF，
∴FM＝DH，
∴AD＝AH+HD＝HM+MF＝HF，
∵HF＝＝＝10，
∴AD＝10．
∵S△EFH＝HE•EF＝HF•EM，
∴EM＝＝，
又∵AE＝EM＝EB，
∴AB＝2EM＝，
∴AD：AB＝10：＝．
故答案为：．

三、解答题（共11小题，计78分．解答题应写出过程）
15．（5分）计算：2cos45°﹣|2﹣3|+（﹣）﹣1+（π﹣3.14）0．
【解答】解：原式＝2×﹣（3﹣2）﹣2+1
＝﹣3+2﹣2+1
＝3﹣4．
16．（5分）化简：（x﹣1﹣）÷．
【解答】解：原式＝×
＝
17．（5分）如图，已知点A是直线l外一点，点B是直线l上一点，请用尺规作⊙O，使得⊙O过点A且与直线l相切于点B．（要求：尺规保留作图痕迹，并把作图痕迹用黑色签字笔加黑）．

【解答】解：如图，⊙O即为所求．

18．（5分）如图，正方形ABCD中，点G在对角线BD上（不与B、D重合），GE⊥DC于点E，GF⊥BC于点F，连接AG，CG．求证AG＝EF．

【解答】证明：∵GE⊥CD，GF⊥BC，
∴∠GEC＝∠GFC＝90°＝∠ECF，
∴四边形GFCE是矩形．
∴EF＝GC．
∵四边形ABCD是正方形，
∴∠ADG＝∠CDG＝45°，AD＝CD．
又DG＝DG，
∴△ADG≌△CDG（SAS）．
∴AG＝CG．
∴AG＝EF．
19．（7分）期末考试后，某市第一中学为了解本校九年级学生期末数学成绩情况，决定对该年级学生期末考试数学考试成绩进行抽样分析，已知九年级共有12个班，每班48名学生．请按要求回答下列问题：
收集数据：
（1）若要从全年级学生中抽取一个96人的样本，你认为以下抽样方法最合理的是　②③　．（只填写序号）
①随机抽取两个班级的96名学生；
②在全年级学生中随机抽取96名学生；
③全年级12个班中分别各随机抽取8名学生；
④从全年级学生中随机抽取96名男生．
整理数据：
（2）将抽取的96名学生的成绩进行分组，绘制频数分布表和成绩分布扇形统计图（不完整）如下，根据图表中数据填空：
①A类成绩的频数为　48　，C类部分的圆心角度数为　60°　；
②估计全年级A、B类学生大约一共有多少名？
成绩（单位：分）
频数
频率
A类（80～100）

0.5
B类（60～79）

0.25
C类（40～59）
16

D类（0～39）
8

分析数据：
（3）第一中学为了解学校教学情况，将第二中学九年级的抽样数据和本校进行对比，得表：
学校
平均分（分）
方差
中位数（分）
第一中学
73
432
80
第一中学
71
497
83
你认为哪所学校的教学效果较好？结合数据，请任选一个角度来解释你的观点．

【解答】解：（1）若要从全年级学生中抽取一个96人的样本，认为以下抽样方法中比较合理：
②在全年级学生中随机抽取96名学生；
③全年级12个班中分别各随机抽取8名学生；
①④都比较片面，
故答案为：②③；
（2）①A类成绩的频数为96×0.5＝48，
C类部分的圆心角度数为360°×＝60°，
故答案为：48、60°；
②估计全年级A、B类学生大约一共有：
12×48×（0.5+0.25）＝432（名）；
（3）第一中学的教学效果较好，
因为第一中学的平均成绩大、方差小，学生总体成绩波动不大．
20．（7分）小华去太华路小学参加中考体育测试时发现，太华路小学的路灯照明是依靠太阳能光板供给的，如图所示，路灯立柱AB长10.3米，支架CO的长为0.4米，支点C到立柱顶端B的距离为0.3米，支架OC与立柱AB的夹角∠OCA＝120°，支架OC与光板DE垂直，太阳能光板DE长为1.2米，点O是DE的中点，求太阳能光板最低点E离地面的高度（结果保留根号），

【解答】解：由题意知，AB＝10.3米，OC＝0.4米，CB＝0.3米，∠OCA＝120°，DE＝1.2米．
∴OE＝DE＝0.6米．
如图，过点E作EH⊥AB于点H，过点O作OM⊥EH于点M，过点C作CN⊥OM于点N，
∴NM＝CH，EG＝AH，∠OCN＝∠OCA﹣90°＝30°，
∴∠CON＝60°，
∴∠EOM＝30°．
在Rt△OCN中，ON＝OC＝×0.4＝0.2（米）．
在Rt△OEM中，OM＝OE•cos∠EOM＝0.6×cos30°＝（米）．
∴MN＝OM﹣ON＝（﹣0.2）米．
∴CH＝MN＝（﹣0.2）米．
∴AH＝AB﹣BC﹣CH＝10.3﹣0.3﹣（﹣0.2）＝（﹣）（米），
∴EG＝AH＝（﹣）（米），
因此，太阳能光板最低点E离地面的高度为（﹣）米．

21．（7分）甲、乙两人用扑克牌玩“10点”游戏，游戏规则如下：
①将牌面数字作为点数，如红桃6的点数就是6（牌面点数与牌的花色无关）；
②每人摸2次，每次摸一张（不放回），将所摸的两张牌的点数相加，若点数之和小于或等于10，此时点数就是最终点数；若点数之和大于10，则最终点数是0；
③游戏结束前双方均不知道对方点数；
④判定游戏结果的依据是：最终点数大的一方获胜，最终点数相等时不分胜负．现在甲已经摸出了两张牌，且这两张牌的数字之和是8，这时桌上还有四张背面朝上的扑克牌，牌面数字分别是4、5、6、7，如图所示．
（1）若乙从桌面上随机摸出一张扑克牌，点数为6的概率是多少？
（2）根据题意和游戏规则，甲乙双方谁获胜的可能大？
【解答】解：（1）若乙从桌面上随机摸出一张扑克牌，点数为6的概率是；
（2）甲乙双方甲获胜的可能大，理由如下：
画树状图如图：

共有12个等可能的结果，甲已经摸出了两张牌，且这两张牌的数字之和是8，乙获胜的结果有4个，
∴乙获胜的概率为＝，
∴甲获胜的可能大．
22．（7分）每年5月，西安郊区的樱桃大量成熟，某樱桃种植户对樱桃的销售价格规定如下：一次购买2千克以下（含2千克）樱桃，单价为a元/千克；一次购买2千克以上，超过2千克部分的樱桃价格打七五折，小华对购买量x（千克）和付款金额y（元）这两个变量的对应关系做了分析，绘制了如图所示的函数图象．请你根据图象回答下列问题．
（1）求y与x的函数关系式：
（2）已知小华将30元钱全部用于购买樱桃，小丽购买了2千克樱桃，如果他们两个人合起来购买，可以比分开购买多买多少千克樱桃？

【解答】解：（1）由图象可得，
a＝40÷2＝20，
当0＜x≤2时，y＝20x，
当x＞2时，销售价格为：20×0.75＝15（元/千克），
则y与x的函数关系式为y＝40+（x﹣2）×15＝15x+10，
即y与x的函数关系式为y＝；
（2）小华购买的樱桃质量为：30÷20＝1.5（千克），
小丽购买樱桃的花费为：2×20＝40（元），
如果他们两个人合起来购买，则可以购买的樱桃质量为：（30+40﹣10）÷15＝4（千克），
4﹣（2+1.5）＝4﹣3.5＝0.5（千克），
即如果他们两个人合起来购买，可以比分开购买多买0.5千克樱桃．
23．（8分）如图，四边形ABCD内接于⊙O，BD是⊙O的直径，过点A作⊙O的切线交CD的延长线于点E，DA平分∠BDE．
（1）求证：AE⊥CD．
（2）若AB＝4，AE＝2，求CD的长．

【解答】解：（1）连接OA，
∵AE是⊙O的切线，
∴OA⊥AE，
即∠OAE＝90°＝∠OAD+∠DAE，
又∵DA平分∠BDE，
∴∠ODA＝∠ADE，
∵OA＝OD，
∴∠ODA＝∠OAD，
∴∠ADE+∠DAE＝90°，
∴∠AED＝180°﹣（∠ADE+∠DAE）＝180°﹣90°＝90°，
∴AE⊥CD；
（2）∵BD是⊙O的直径，
∴∠BAD＝90°＝∠AED，
又∵∠ADE＝∠ADB，
∴△ABD∽△EAD，
∴＝＝＝sin∠DAE，
∴∠DAE＝30°，
在Rt△ADE中，AE＝2，∠DAE＝30°，
∴DE＝AE•tan∠DAE＝2×tan30°＝，
∴∠ADE＝90°﹣30°＝60°＝∠ABC，
∴∠CBD＝∠ABD＝30°，
∴CD＝AD＝2DE＝．

24．（10分）已知抛物线L1过点A（﹣1，0）、B（3，0）、C（0，﹣3）．
（1）求该抛物线的表达式．
（2）抛物线L1的对称轴与x轴交于点P，将该抛物线沿直线y＝m翻折得抛物线L2，在抛物线L2第四象限的图象上是否存在一点D，使的△CPD是以CP为直角边的等腰直角三角形？若存在，求出满足条件的L2的解析式；若不能，请说明理由．

【解答】解：（1）设抛物线L1的解析式为y＝ax2+bx+c，将A（﹣1，0）、B（3，0）、C（0，﹣3）代入y＝ax2+bx+c，
得，解得，
∴该抛物线的解析式为y＝x2﹣2x﹣3．
（2）存在．
如图，作CD⊥PC，使CD＝PC，且点D在第四象限；作DE⊥y轴于点E．

由y＝x2﹣2x﹣3＝（x﹣1）2﹣4，得该抛物线的顶点坐标为（1，﹣4），点P的坐标为（1，0）．
∴抛物线L1沿直线y＝m翻折后得到的抛物线L2的顶点坐标为（1，2m+4），
∴抛物线L2的解析式为y＝﹣（x﹣1）2+2m+4＝﹣x2+2x+2m+3．
∵∠CED＝∠POC＝∠PCD＝90°，
∴∠ECD＝90°﹣∠PCO＝∠OPC，
又∵CD＝PC，
∴△CED≌△POC（AAS），
∴CE＝PO＝1，ED＝OC＝3，
∴D（3，﹣4），
∵点D在抛物线L2上，
∴﹣9+6+2m+3＝﹣4，
解得m＝﹣2，
∴抛物线L2的解析式为y＝﹣x2+2x﹣1．
25．（12分）圆的定义：在同一平面内，到定点的距离等于定长的所有点所组成的图形．
（1）已知：如图1，OA＝OB＝OC，请利用圆规画出过A、B．C三点的圆．若∠AOB＝70°，则∠ACB＝　35°　．
如图，Rt△ABC中，∠ABC＝90°，∠BCA＝30°，AB＝2．
（2）已知，如图2．点P为AC边的中点，将AC沿BA方向平移2个单位长度，点A、P、C的对应点分别为点D、E、F，求四边形BDFC的面积和∠BEA的大小．
（3）如图3，将AC边沿BC方向平移a个单位至DF，是否存在这样的a，使得直线DF上有一点Q，满足∠BQA＝45°且此时四边形BADF的面积最大？若存在，求出四边形BADF面积的最大值及平移距离a，若不存在，说明理由．

【解答】（1）以O为圆心，OA为半径作辅助圆，如图，
，
∵∠AOB＝70°，
∴∠ACB＝35°，
故答案为35°．
（2）连接PB，PE，如图，
，
Rt△ABC中，∠ABC＝90°，∠BCA＝30°，AB＝2．
∴AC＝4，∠BAC＝60°，BC＝2．
∵P为Rt△ABC斜边AC中点，
∴BP＝＝2，
线段AC平移到DF之后，AB＝AD＝PE＝2，BP＝AE＝2，
∴四边形ABPE为菱形，
∵∠BAC＝60°，
∴∠BEA＝30°，
∵CF∥BD，且∠ABC＝90°，
∴四边形BDFC为直角梯形，
∴S＝（BD+CF）×BC＝×6×2＝6，
（3）如图所示，

当AC边沿BC方向平移2个单位至DF时，
满足∠BQA＝45°且此时四边形BADF的面积最大，
此时直角梯形ABFD的最大面积为，
S＝＝＝4+．