吉林省松原市乾安县2021-2022学年八年级下学期期中教学质量检测数学试卷(含解析)

这是一份吉林省松原市乾安县2021-2022学年八年级下学期期中教学质量检测数学试卷(含解析)，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

吉林省松原市乾安县2021-2022学年八年级下学期期中
数学试题
一、选择题
1. 下列二次根式，化简后能与合并的是（ ）
A. B. C. D.
2. 直角三角形的两边长分别为6和10，那么它的第三边的长度为（）
A. 8 B. 10 C. 8或 D. 10或
3. 下列命题正确的是（ ）
A. 对角线相等的四边形是平行四边形 B. 对角线相等的四边形是矩形
C. 对角线互相垂直的平行四边形是菱形 D. 对角线互相垂直且相等的四边形是正方形
4. 下列运算不正确是（ ）
A. B.
C. D.
5. 如图，矩形ABCD的对角线AC，BD交于点O，AC＝4cm，∠AOD＝120°，则BC的长为（ ）cm．

A. B. 4 C. D. 2
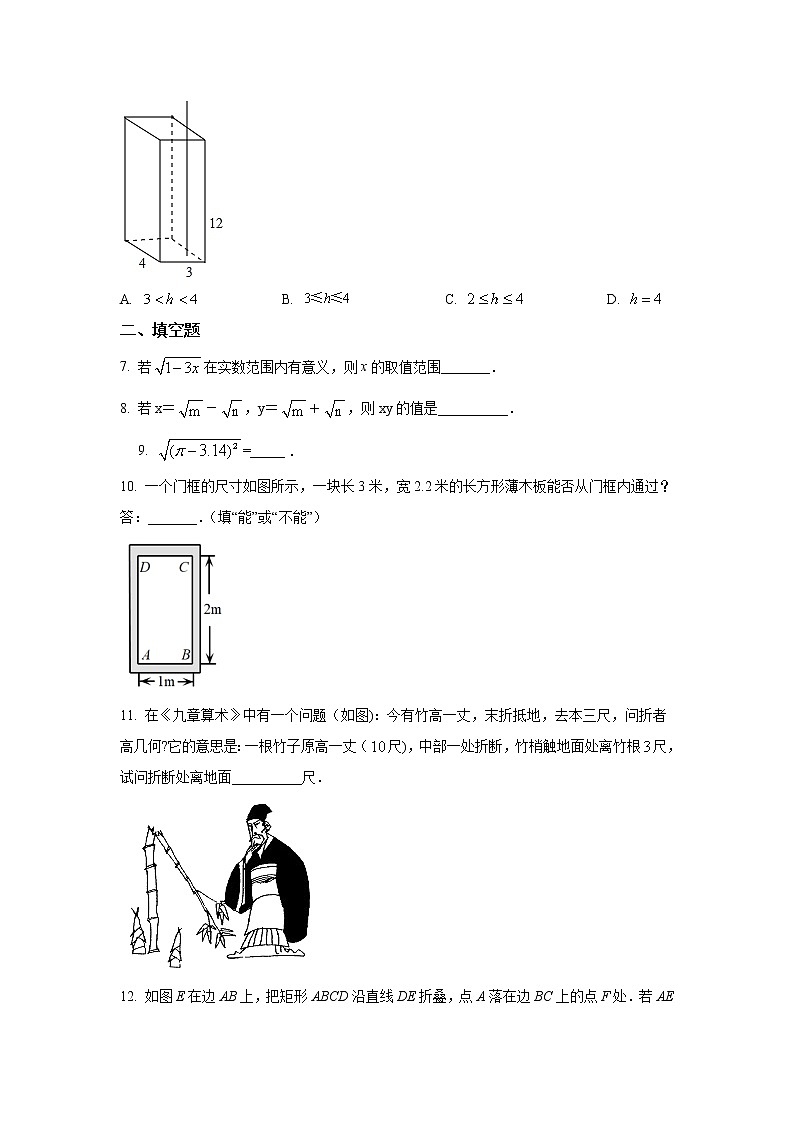
6. 如图，是一种饮料的包装盒，长、宽、高分别为、、，现有一长为的吸管插入盒的底部，则吸管漏在盒外面的部分的取值范围为（ ）

A. B. C. D.
二、填空题
7. 若在实数范围内有意义，则x的取值范围_______．
8. 若x＝－，y＝＋，则xy的值是__________．
9. =_____．
10. 一个门框的尺寸如图所示，一块长3米，宽2.2米的长方形薄木板能否从门框内通过？答：_______．（填“能”或“不能”）

11. 在《九章算术》中有一个问题（如图)：今有竹高一丈，末折抵地，去本三尺，问折者高几何?它的意思是：一根竹子原高一丈（尺)，中部一处折断，竹梢触地面处离竹根尺，试问折断处离地面__________尺．

12. 如图E在边AB上，把矩形ABCD沿直线DE折叠，点A落在边BC上的点F处．若AE＝5，BF＝3．则△CDF的面积是__．

13. 如图，在等腰Rt△OAA1中，∠OAA1=90°，OA=1，以OA1为直角边作等腰Rt△OA1A2，以OA2为直角边作等腰Rt△OA2A3，…，则OAn的长度为__．

14. 已知如图，四边形ABCD为矩形，点O是AC中点，过点O的一直线分别与AB、CD交于点E、F，连接BF交AC于点M，连接DE、BO，若∠COB＝60°，FO＝FC，则下列结论：①FB⊥OC，OM＝CM；②△EOB≌△CMB；③四边形EBFD是菱形；④MB：OE＝3：2，其中正确结论是_____．

三、解答题
15. 计算：
（1）；
（2）．
16. 如图17－Z－11，小红同学要测量A，C两地的距离，但A，C之间有一水池，不能直接测量，于是她在A，C同一水平面上选取了一点B，点B可直接到达A，C两地．她测量得到AB＝80米，BC＝20米，∠ABC＝120°.请你帮助小红同学求出A，C两地之间的距离．(结果精确到1米，参考数据：≈4.6)

图17－Z－11
17. 如图，四边形ABCD是平行四边形，E、F是对角线AC上的两点，且AE＝CF，顺次连接B、E、D，F．求证：四边形BEDF是平行四边形．

18. 如图，E是正方形ABCD对角线BD上一点．连接AE，CE，并延长CE交AD于点F．若∠AEC＝140°，求∠DFE的度数．

19. 如图，ABC的三个顶点在正方形网格的格点上，网格中的每个小正方形的边长均为单位1．

（1）求证：ABC为直角三角形；
（2）在图中画一条线段DE，使DE=AB，且D、E两点落在正方形网格的格点上；
（3）求点B到AC的距离．
20. 小王与小林进行遥控赛车游戏，终点为点A，小王的赛车从点C出发，以4米/秒的速度由西向东行驶，同时小林的赛车从点B出发，以3米/秒的速度由南向北行驶（如图）．已知赛车之间的距离小于或等于25米时，遥控信号会产生相互干扰，AC＝40米，AB＝30米．出发3秒钟时，遥控信号是否会产生相互干扰？

21. 如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF⊥AB，OG∥EF．
（1）求证：四边形OEFG是矩形；
（2）若AD=10，EF=4，求OE和BG的长．

22. 已知：如图，平行四边形ABCD中，M、N分别为AB和CD的中点．
（1）求证：四边形AMCN是平行四边形；
（2）当AC、BC满足怎样的数量关系时，四边形AMCN是矩形，请说明理由．

23. 阅读下列解题过程：
＝＝﹣1；＝＝﹣；
＝＝﹣；……则：
（1）＝　　；＝　　；
（2）观察上面解题过程，请直接写出式子＝　　；
（3）利用这一规律计算：（+++……+）•（+1）的值．
24. 教材呈现：下图是华师版八年级下册数学教材第111页的部分内容．


（1）问题解决：请结合图①，写出例1的完整解答过程．
（2）问题探究：在菱形ABCD中，对角线AC、BD相交于点O，AB＝4，∠BAD＝2∠ABC．过点D作DE//AC交BC的延长线于点E．如图②，连结OE，则OE的长为____．
（3）如图③，若点P是对角线BD上的一个动点，连结PC、PE，则PC＋PE的最小值为_____．
25. 操作发现
将一副直角三角板如图①摆放，能够发现等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合．
问题解决
将图①中的等腰直角三角板ABC绕点B顺时针旋转30°，点C落在BF上，AC与BD交于点O，连接CD，如图②．

（1）求证：△CDO是等腰三角形；
（2）若DF=8，求AD长．
26. 如图1，在正方形ABCD中，点E在AD延长线上，P是对角线BD上的一点，且点P位于AE的垂直平分线上，PE交CD于点F．

（1）猜测PC和PE有什么大小及位置关系，并给出证明．
（2）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，∠ABC＝120°时，连接CE，试探究线段AP与线段CE的数量关系．并说明理由．
答案

1. D
解：A. 是最简二次根式，且不能与合并，故本选项错误；
B. 是最简二次根式，且不能与合并，故本选项错误；
C. 是最简二次根式，且不能与合并，故本选项错误；
D. 化为最简二次根式后能与合并，故本选项正确．
故选：D
2. C
解：当10为直角边时，斜边=；
当10为斜边时，另-条直角边= =8．
故选C．
3. C
解：A、对角线互相平分的四边形是平行四边形，选项错误，不符合题意；
B、对角线相等平行四边形是矩形，选项错误，不符合题意；
C、对角线互相垂直的平行四边形是菱形，选项正确，符合题意；
D、对角线互相垂直且相等的平行四边形是正方形，选项错误，不符合题意；
故选C
4. ABD
解：A、，运算不正确，符合题意；
B、，运算不正确，符合题意；
C、，运算正确，不符合题意；
D、，运算错误，符合题意；
故选：ABD．
5. C
解：∵矩形ABCD的对角线AC，BD交于点O，AC=4cm，
∴OA=OB=AC=2cm．
又∵∠AOD=120°，
∴∠AOB=60°，
∴△AOB是等边三角形，
∴AB=OA=OB=2cm．
∴在直角△ABC中，∠ABC=90°，AB=2cm，AC=4cm，
∴BC=(cm)．
故选：C．
6. B
①当吸管放进杯里垂直于底面时露在杯口外的长度最长，最长为16−12＝4（cm）；
②露出部分最短时与底面对角线和高正好组成直角三角形，
底面对角线长==5cm，高为12cm，
由勾股定理可得：杯里面管长=＝13cm，则露在杯口外的长度最短为16−13＝3（cm），
∴
故选：B．
7.
解：根据二次根式被开方数必须是非负数的条件，要使在实数范围内有意义，必须
解得：．
故答案为：．
8. m-n
由题意xy=
故答案为m-n.
9. π﹣3.14
解：，由于π=3.14159…＞3.14，故原式=π﹣3.14，
故答案为π﹣3.14.
10. 能
解：连接，如图所示：

在中，根据勾股定理可得：，
又∵，
∴木板的宽，
∴木板能从门框内通过．
故答案为：能．
11. 4.55
解：设折断处离地面尺，根据题意可得：
，
解得：，
答：折断处离地面4.55尺．
故答案为：4.55．
12. 54

解：设BC为x则AD=FD=x．
∵矩形ABCD沿直线DE折叠，点A落在边BC上的点F处，
∴AE=EF=5
∵在RtEBF中，BF=3
∴BE=4
∴AB=CD=9
在RtFCD中，FC=x-3，CD=9，FD=x
由勾股定理可得
解得x=15
∴
故答案为：54．
13.
∵△OAA1为等腰直角三角形，OA=1，
∴AA1=OA=1，OA1=OA=；
∵△OA1A2为等腰直角三角形，
∴A1A2=OA1=，OA2=OA1=2；
∵△OA2A3为等腰直角三角形，
∴A2A3=OA2=2，OA3=OA2=2；
∵△OA3A4为等腰直角三角形，
∴A3A4=OA3=2，OA4=OA3=4．
∵△OA4A5为等腰直角三角形，
∴A4A5=OA4=4，OA5=OA4=4．
∵△OA5A6为等腰直角三角形，
∴A5A6=OA5=4，OA6=OA5=8．
∴OAn=．
14. ①③④
连接BD，

∵四边形ABCD是矩形，
∴AC＝BD，AC、BD互相平分，
∵O为AC中点，
∴BD也过O点，
∴OB＝OC，
∵∠COB＝60°，OB＝OC，
∴△OBC等边三角形，
∴OB＝BC＝OC，∠OBC＝60°，
在△OBF与△CBF中
，
∴△OBF≌△CBF（SSS），
∴△OBF与△CBF关于直线BF对称，
∴FB⊥OC，OM＝CM；
∴①正确，
∵∠OBC＝60°，
∴∠ABO＝30°，
∵△OBF≌△CBF，
∴∠OBM＝∠CBM＝30°，
∴∠ABO＝∠OBF，
∵AB∥CD，
∴∠OCF＝∠OAE，
∵OA＝OC，
易证△AOE≌△COF，
∴OE＝OF，
∴OB⊥EF，
∴四边形EBFD是菱形，
∴③正确，
∵△EOB≌△FOB≌△FCB，
∴△EOB≌△CMB错误．
∴②错误，
∵∠OMB＝∠BOF＝90°，∠OBF＝30°，
∴MB＝，OF＝，
∵OE＝OF，
∴MB：OE＝3：2，
∴④正确；
故答案为①③④
15. （1），
，
，
；
（2），
，
，
．
16.解：过点C作CD⊥AB交AB的延长线于点D，
∵∠ABC＝120°，∴∠CBD＝60°，
∴在Rt△BCD中，∠BCD＝90°－∠CBD＝30°，
∴BD＝BC＝×20＝10(米)，
∴CD＝＝10 (米)，
AD＝AB＋BD＝80＋10＝90(米)．
在Rt△ACD中，AC＝＝≈92(米)．
答：A，C两地之间的距离约为92米
17. 证明：连接BD，交AC于点O，如图所示：

∵四边形ABCD是平行四边形
∴OA＝OC，OB＝OD
∵AE＝CF
∴OA﹣AE＝OC﹣CF
即OE＝OF
∴四边形DEBF是平行四边形．
18. 解：∵四边形ABCD是正方形，
∴AB＝CB，∠ABE＝∠CBE＝∠ADB＝45°．
在△ABE和△CBE中，
，
∴△ABE≌△CBE，
∴∠AEB＝∠CEB．
又∵∠AEC＝140°，
∴∠CEB＝70°．
∵∠DEC＋∠CEB＝180°，
∴∠DEC＝180°－∠CEB＝110°．
∵∠DFE＋∠ADB＝∠DEC，
∴∠DFE＝∠DEC－∠ADB＝110°－45°＝65°．
19. （1）
由勾股定理得，
AB＝，
BC＝，
AC＝，
∵
∴AB+BC＝AC
∴△ABC为直角三角形；
（2）
根据题意所画如下图，答案不唯一；

（3）
设B到AC的距离为h ，
由得，
，
解得h＝，
∴点B到AC的距离为．
20. 解：如图，出发3秒钟时，米，米，
∵AC=40米，AB=30米，
∴AC1=28米，AB1=21米，
∴在中，米＞25米，
∴出发3秒钟时，遥控信号不会产生相互干扰．

21. 解：(1)证明:∵四边形ABCD为菱形，
∴点O为BD的中点，
∵点E为AD中点，
∴OE为△ABD的中位线，
∴OE∥FG，
∵OG∥EF，∴四边形OEFG为平行四边形
∵EF⊥AB，∴平行四边形OEFG为矩形．
(2)∵点E为AD中点，AD=10，
∴AE=
∵∠EFA=90°，EF=4，
∴在Rt△AEF中，．
∵四边形ABCD为菱形，
∴AB=AD=10，
∴OE=AB=5，
∵四边形OEFG矩形，
∴FG=OE=5，
∴BG=AB-AF-FG=10-3-5=2．
故答案为：OE=5，BG=2．
22. （1）证明∵四边形ABCD是平行四边形
∴AB＝CD，AB∥CD
∵M，N分别为AB和CD的中点
∴AMAB，CNCD
∴AM＝CN，且AB∥CD
∴四边形AMCN是平行四边形
（2）答：AC=BC时，四边形AMCN是矩形
证明∵AC=BC，且M是BC的中点
∴CM⊥AB
即∠AMC＝90°
∴四边形AMCN是矩形
23. （1）
解：
＝
＝﹣
＝﹣3；

＝
＝10﹣3；
（2）
（2）观察上面的解题过程，请直接写出式子＝﹣；
（3）
（3）原式＝（﹣1+﹣+﹣+…+﹣）•（+1）
＝2022﹣1
＝2021
24. （1）
四边形ABCD是菱形，
∴AD//BC，
．
，
．
四边形ABCD是菱形，
．
是等边三角形．
（2）
四边形ABCD是菱形，
∴AD//BC，
又∵DE//AC，
四边形ACED是平行四边形，
由（1）可得，
故四边形ACED是菱形；
则，，∠BDC=30°，OA=2，


则．
（3）
如图所示，过A作BE的垂线交BE于点F，连接AE，
A点关于BD的对称点为点C，
则PC＋PE的最小值为AE；
为等边三角形，
，
，，

则PC＋PE的最小值为．

25. 解：（1）证明：由图①知BC=DE，
∴∠BDC=∠BCD．
∵∠DEF=30°，
∴∠BDC=∠BCD=75°．
∵∠ACB=45°，
∴∠DOC=30°+45°=75°．
∴∠DOC=∠BDC．
∴△CDO是等腰三角形．
（2）作AG⊥BC，垂足为点G，DH⊥BF，垂足为点H，

在Rt△DHF中，∠F=60°，DF=8，
∴DH=4，HF=4．
在Rt△BDF中，∠F=60°，DF=8，
∴DB=8，BF=16．
∴BC=BD=8．
∵AG⊥BC，∠ABC=45°，
∴BG=AG=4．
∴AG=DH．
∵AG∥DH，
∴四边形AGHD为矩形．
∴AD=GH=BF﹣BG﹣HF=16﹣4﹣4=12﹣4．
26. （1）PC=PE，PC⊥PE
证明∵点P位于AE的垂直平分线上，
∴PA=PE，
∴∠PAD=∠E，
∵四边形ABCD是正方形，
∴AD=DC，∠ADB=∠CDB，
∵PD=PD，
∴△ADP≌△CDP（SAS）
∴PA=PC，∠PAD=∠PCD，
∴PC=PE，∠PCD=∠E，
∵∠PFC=∠DFE，
∴∠CPF=∠FDE，
∵四边形ABCD是正方形，
∴∠ADC=90°，
∴∠FDE=90°，
∴∠CPF=90°，
∴PC⊥PE．
（2）PA=CE．理由如下：
证明：∵点P位于AE的垂直平分线上，
∴PA=PE，
∴∠PAD=∠E，
∵四边形ABCD是菱形，
∴AD=DC，∠ADB=∠CDB，
∵PD=PD，
∴△ADP≌△CDP（SAS）
∴PA=PC，∠PAD=∠PCD，
∴PC=PE，∠PCD=∠E，
∵∠PFC=∠DFE，
∴∠CPF=∠FDE，
∵四边形ABCD是菱形，∠ABC=120°
∴∠ADC=∠ABC=120°
∴∠EDF=180°-∠ADC=60°
∴∠CPF=60°
∵PE=PC
∴△PCE是等边三角形
∴CE=PE
∴AP=CE．