2023年中考数学精选真题实战测试38 平行四边形 B

这是一份2023年中考数学精选真题实战测试38 平行四边形 B，共14页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
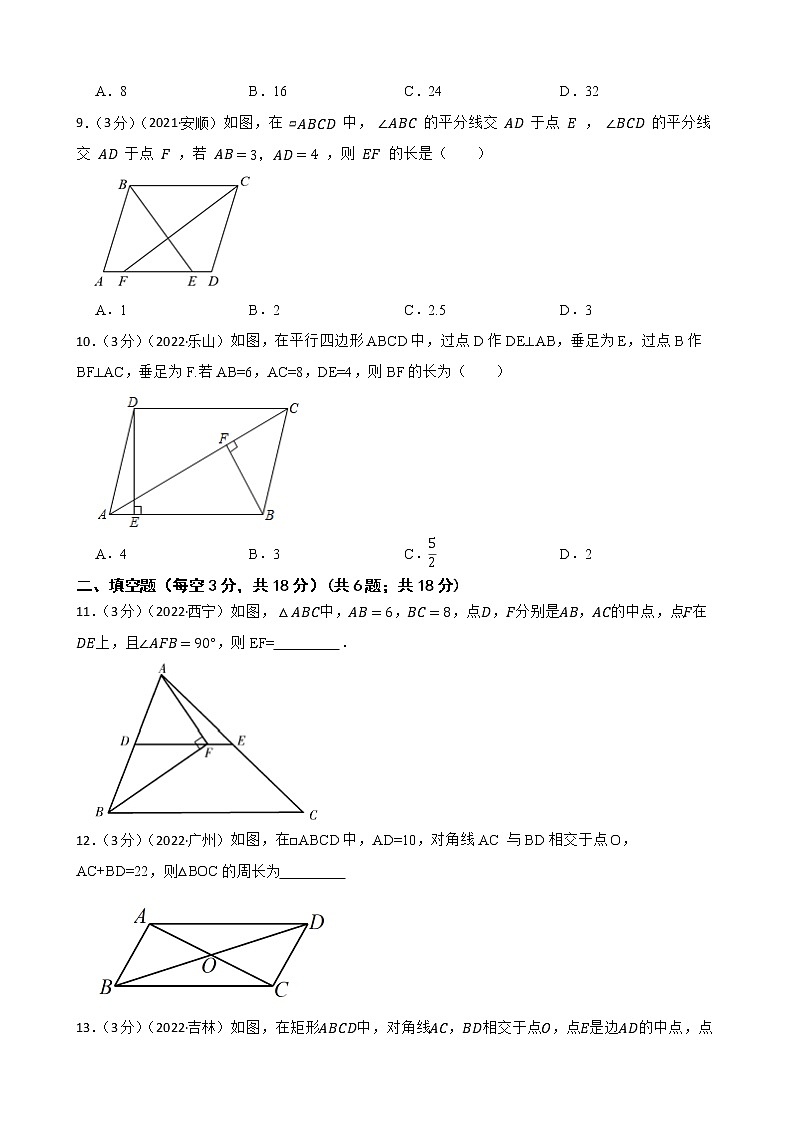
 2023年中考数学精选真题实战测试38 平行四边形 B一、单选题（每题3分，共30分）(共10题；共30分)1．（3分）（2022·广东）如图，在 中，一定正确的是（　　）  A． B． C． D．2．（3分）（2022·广东）如图，在 中， ，点D，E分别为 ， 的中点，则 （　　）  A． B． C．1 D．23．（3分）（2022·益阳）如图，在▱ABCD中，AB＝8，点E是AB上一点，AE＝3，连接DE，过点C作CF∥DE，交AB的延长线于点F，则BF的长为（　　）A．5 B．4 C．3 D．24．（3分）（2022·内江）如图，在▱ABCD中，已知AB＝12，AD＝8，∠ABC的平分线BM交CD边于点M，则DM的长为（　　）A．2 B．4 C．6 D．85．（3分）（2022·恩施）如图，在四边形ABCD中，∠A=∠B=90°，AD=10cm，BC=8cm，点P从点D出发，以1cm/s的速度向点A运动，点M从点B同时出发，以相同的速度向点C运动，当其中一个动点到达端点时，两个动点同时停止运动.设点P的运动时间为t（单位：s），下列结论正确的是（　　）A．当时，四边形ABMP为矩形B．当时，四边形CDPM为平行四边形C．当时，D．当时，或6s6．（3分）（2022·河南）如图，在菱形ABCD中，对角线AC，BD相交于点O，点E为CD的中点.若OE＝3，则菱形ABCD的周长为（　　）A．6 B．12 C．24 D．487．（3分）（2022·湘潭）在▱ABCD中（如图），连接AC，已知∠BAC=40°，∠ACB=80°，则∠BCD=（　　）A．80° B．100° C．120° D．140°8．（3分）（2022·嘉兴）如图，在△ABC中，AB＝AC＝8，点E，F，G分别在边AB，BC，AC上，EF∥AC，GF∥AB，则四边形AEFG的周长是（　　）A．8        B．16      C．24       D．329．（3分）（2021·安顺）如图，在 中， 的平分线交 于点 ， 的平分线交 于点 ，若 ，则 的长是（　　）  A．1 B．2 C．2.5 D．310．（3分）（2022·乐山）如图，在平行四边形ABCD中，过点D作DE⊥AB，垂足为E，过点B作BF⊥AC，垂足为F.若AB=6，AC=8，DE=4，则BF的长为（　　）A．4 B．3 C． D．2二、填空题（每空3分，共18分）(共6题；共18分)11．（3分）（2022·西宁）如图，中，，，点，分别是，的中点，点在上，且，则EF=　     　．12．（3分）（2022·广州）如图，在□ABCD中，AD=10，对角线AC 与BD相交于点O，AC+BD=22，则△BOC的周长为　     　13．（3分）（2022·吉林）如图，在矩形中，对角线，相交于点，点是边的中点，点在对角线上，且，连接．若，则　     　．14．（3分）（2022·扬州）“做数学”可以帮助我们积累数学活动经验.如图，已知三角形纸片，第1次折叠使点落在边上的点处，折痕交于点；第2次折叠使点落在点处，折痕交于点.若，则　     　.15．（3分）（2021·盘锦）如图，四边形ABCD是平行四边形，以点B为圆心，BC的长为半径作弧交AD于点E，分别以点C，E为圆心，大于 的长为半径作弧，两弧交于点P，作射线BP交AD的延长线于点F，∠CBE＝60°，BC＝6，则BF的长为　     　16．（3分）（2022·攀枝花）如图，以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论：①四边形是平行四边形；②当时，四边形是矩形；③当时，四边形是菱形；④当，且时，四边形是正方形.其中正确结论有　         　（填上所有正确结论的序号）.三、解答题（共8题，共72分）(共8题；共72分)17．（8分）（2022·无锡）如图，在▱ABCD中，点O为对角线BD的中点，EF过点O且分别交AB、DC于点E、F，连接DE、BF.求证：（1）（4分）△DOF≌△BOE；（2）（4分）DE=BF.18．（8分）（2022·扬州）如图，在中，分别平分，交于点.（1）（4分）求证：；（2）（4分）过点作，垂足为.若的周长为56，，求的面积.19．（8分）（2022·新疆）在中，点D，F分别为边AC，AB的中点.延长DF到点E，使，连接BE.（1）（4分）求证：；（2）（4分）求证：四边形BCDE是平行四边形.20．（8分）（2022·株洲）如图所示，点在四边形的边上，连接，并延长交的延长线于点，已知，.（1）（4分）求证：；（2）（4分）若，求证：四边形为平行四边形.21．（8分）（2022·温州）如图，在△ABC 中，  AD⊥BC于点D、E、F分别是AC、AB 的中点，O是 DF 的中点， EO 的延长线交线段 BD 于点G，连结  DE、EF、FG．（1）（4分）求证：四边形 DEFG 是平行四边形．（2）（4分）当AD=5，tan∠EDC==时，求 FG 的长．22．（8分）（2022·永州）如图，是平行四边形的对角线，平分，交于点.（1）（4分）请用尺规作的角平分线，交于点（要求保留作图痕迹，不写作法，在确认答案后，请用黑色笔将作图痕迹再填涂一次）：（2）（4分）根据图形猜想四边形为平行四边形，请将下面的证明过程补充完整.证明：∵四边形是平行四边形，∴∵      ▲      .（两线平行，内错角相等）.又∵平分，平分，∴，∴.∴      ▲      （　　）（填推理的依据）又∵四边形是平行四边形.∴.∴四边形为平行四边形（　　）（填推理的依据），23．（12分）（2022·贵阳）小红根据学习轴对称的经验，对线段之间、角之间的关系进行了拓展探究.如图，在中，为边上的高，，点在边上，且，点是线段上任意一点，连接，将沿翻折得.（1）（4分）问题解决：如图①，当，将沿翻折后，使点与点重合，则　     　；（2）（4分）问题探究：如图②，当，将沿翻折后，使，求的度数，并求出此时的最小值；（3）（4分）拓展延伸：当，将沿翻折后，若，且，根据题意在备用图中画出图形，并求出的值.24．（12分）（2021·沈阳）如图，平面直角坐标系中，O是坐标原点，直线经过点，与x轴交于点A，与y轴交于点B．线段平行于x轴，交直线于点D，连接，．（1）（1分）填空：　     　．点A的坐标是（　     　，　     　）；（2）（4分）求证：四边形是平行四边形；（3）（5分）动点P从点O出发，沿对角线以每秒1个单位长度的速度向点D运动，直到点D为止；动点Q同时从点D出发，沿对角线以每秒1个单位长度的速度向点O运动，直到点O为止．设两个点的运动时间均为t秒．①当时，的面积是      ▲      ．②当点P，Q运动至四边形为矩形时，请直接写出此时t的值．
答案解析部分1．【答案】C2．【答案】D3．【答案】C4．【答案】B5．【答案】D6．【答案】C7．【答案】C8．【答案】B9．【答案】B10．【答案】B11．【答案】112．【答案】2113．【答案】14．【答案】615．【答案】16．【答案】①②③④17．【答案】（1）证明：∵四边形ABCD是平行四边形，O是BD的中点， ∴AB∥DC，OB=OD，∴∠OBE=∠ODF.在△BOE和△DOF中， ，∴△BOE≌△DOF（ASA）（2）证明：∵△BOE≌△DOF， ∴EO=FO，∵OB=OD，∴四边形BEDF是平行四边形.∴DE=BF.18．【答案】（1）证明：在中，∵，∴，∵分别平分，，∴，在和中，∵∴，∴，∴.（2）解：如图，作，∵的周长为56，∴，∵平分，∴，∴.19．【答案】（1）证明：∵点F为边AB的中点，∴，在与中，，∴；（2）证明：∵点D为边AC的中点，∴，由（1）得，∴，，∴，，∴四边形BCDE是平行四边形.20．【答案】（1）证明：∵与是对顶角，∴，在与中，，∴（2）证明：由（1）知，∴，∴，∵点在的延长线上，∴，又∵，∴四边形为平行四边形.21．【答案】（1）证明：∵E，F分别是 的中点， ∴ ，∴ ．∵O是 的中点，∴ ，∴ ，∴ ，∴四边形 是平行四边形．（2）解：∵ ，E是 中点， ∴ ，∴ ，∴ ，∴ ．∵ ，∴ ．∴ ．由 得 ．22．【答案】（1）解：（1）如图，

DE就是所求作的图形.（2）证明：∵四边形是平行四边形， ∴∵.（两线平行，内错角相等）.又∵平分，平分，∴，∴.∴（内错角相等，两线平行）（填推理的依据）又∵四边形是平行四边形.∴.∴四边形为平行四边形（两组对边分别平行的四边形是平行四边形）（填推理的依据）23．【答案】（1）（2）解：，， 是等腰直角三角形，，，，，，，，，是等腰直角三角形，为底边上的高，则点在边上，当时，取得最小值，最小值为；（3）解：如图，连接， ，则，设， 则，，折叠，，，，，，，，，，，在中，，，延长交于点，如图，，，，，，在中，，，.24．【答案】（1）-3；5；0（2）证明：线段平行于轴，点的纵坐标与点一样，又点在直线上，当时，，即，，，，又，四边形是平行四边形；（3）解：①12；②，当时，，当时，，当点，运动至四边形为矩形时，，，当时，，解得，当时，，解得，综上，当点，运动至四边形为矩形时的值为或．