

2022-2023学年河南省郑州市第四高级中学高二上学期期末数学试题(解析版)
展开2022-2023学年河南省郑州市第四高级中学高二上学期期末数学试题
一、单选题
1.已知圆的一般方程为,其圆心坐标是( )
A. B. C. D.
【答案】C
【分析】根据圆的方程即得.
【详解】因为圆的圆心为,
则圆的圆心坐标是.
故选:C.
2.下列四个数中,属于数列中的一项是( )
A.380 B.392 C.321 D.232
【答案】A
【分析】分别令选项中的数值等于,求出是自然数时的这一项,即可得到答案.
【详解】由题意,令,解得,所以A是正确的;
再令均无整数解,所以B、C、D都不正确,
故选:A.
3.在直三棱柱中,若,,,则( )
A. B. C. D.
【答案】C
【分析】根据空间向量线性运算的性质进行求解即可.
【详解】由已知得,
故选:C
4.已知直线,,若,则实数的值为( )
A.1 B. C. D.
【答案】A
【分析】利用一般式下两直线垂直的充要条件“”即可求解
【详解】由.
故选:A.
5.等比数列,…的第四项等于( )
A.-24 B.0 C.12 D.24
【答案】A
【详解】由x,3x+3,6x+6成等比数列得
选A.
【解析】该题主要考查等比数列的概念和通项公式,考查计算能力.
6.已知曲线的方程为(),若曲线是焦点在轴上的双曲线,则实数的取值范围是( )
A. B. C.或5 D.
【答案】D
【分析】根据焦点在轴上的双曲线的方程特征进行求解即可.
【详解】若曲线是焦点在轴上的双曲线,则,解得.
故选:D.
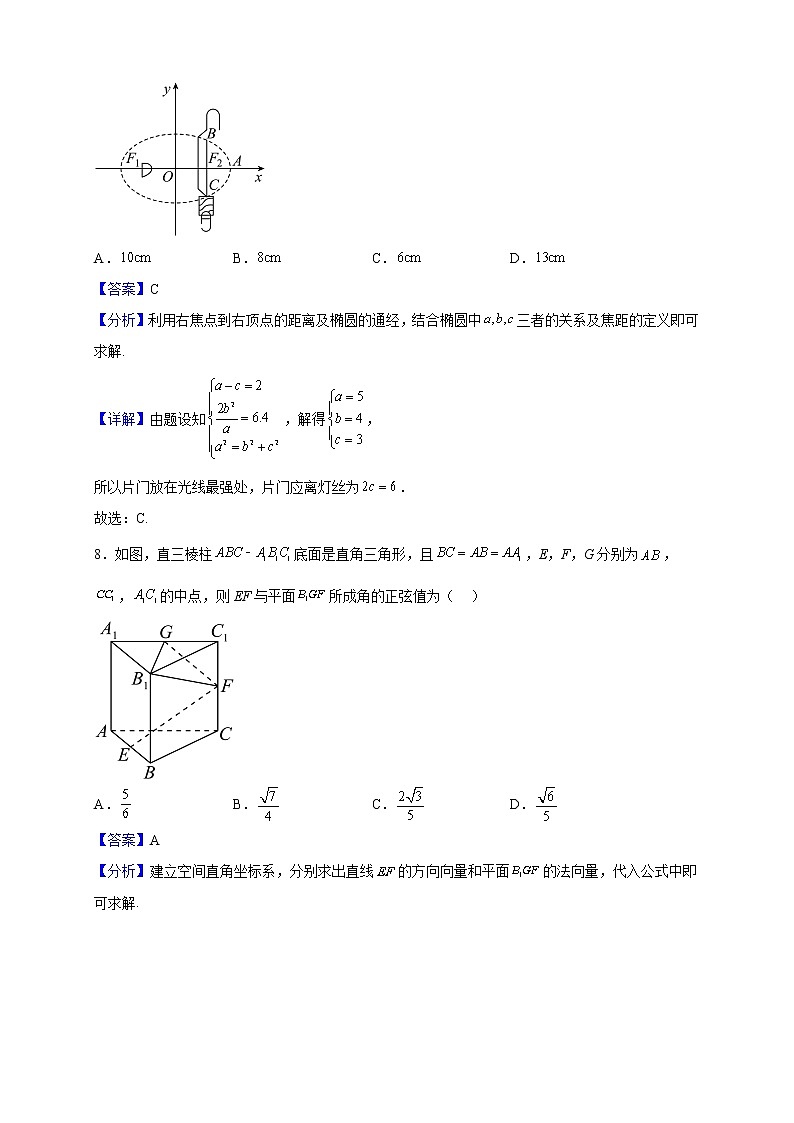
7.椭圆具有这样的光学性质:从椭圆的一个焦点发出的光线,经过椭圆反射后,反射光线都经过椭圆的另一焦点.电影放映机聚光灯泡的反射镜轴截面是椭圆的一部分,灯丝(看成一个点)在椭圆的右焦点处,灯丝与反射镜的顶点的距离,过焦点且垂直于轴的弦,在轴上移动电影机片门,将其放在光线最强处,则片门应离灯丝( )
A. B. C. D.
【答案】C
【分析】利用右焦点到右顶点的距离及椭圆的通经,结合椭圆中三者的关系及焦距的定义即可求解.
【详解】由题设知,解得,
所以片门放在光线最强处,片门应离灯丝为.
故选:C.
8.如图,直三棱柱底面是直角三角形,且,E,F,G分别为,,的中点,则EF与平面所成角的正弦值为( )
A. B. C. D.
【答案】A
【分析】建立空间直角坐标系,分别求出直线的方向向量和平面的法向量,代入公式中即可求解.
【详解】
设,则,分别以,,所在的直线为轴、轴、轴建立空间直角坐标系,
则,,,,,,
则,,,
设平面的法向量为,则取,则,,故为平面的一个法向量,
设EF与平面所成角为,则,
∴与平面所成角的正弦值为.
故选:A.
9.已知抛物线:的焦点为,点在抛物线上,为坐标原点,若,则的面积为( )
A. B. C. D.
【答案】C
【分析】过点作准线的垂线,垂足为.过点作直线的垂线,垂足为,由条件得,求出,即可求出直线的方程与抛物线联立,即可求出的坐标,则表示出的面积代入即可得出答案.
【详解】依题意作图.抛物线的准线方程为,过点作准线的垂线,
垂足为.过点作直线的垂线,垂足为,由条件得,
设,则,,
直线的方程为:,由于点在抛物线上,,
解得或(不符合题意,舍),
,所以,
.
故选:C.
10.直线与曲线恰有两个交点,则实数取值范围是( )
A. B. C. D.
【答案】B
【分析】根据已知条件及直线与圆相切的充要条件,结合点到直线的距离公式即可求解.
【详解】曲线表示圆在轴的上半部分,
当直线与圆相切时,,解得,
当点在直线上时,,可得,
所以实数取值范围为.
故选:B.
11.过双曲线的右支上的一点P分别向圆和圆作切线,切点分别为M,N,则的最小值为( )
A.8 B.9 C.10 D.11
【答案】B
【分析】由切线,展开根据双曲线的定义以及双曲线的性质即可求解.
【详解】设双曲线的左、右焦点分别为,
.
故选:B
12.等差数列的前项和为,若,则满足的最小的正整数的值为( )
A.31 B.32 C.33 D.34
【答案】C
【分析】根据等差数列等差中项的概念及推论,结合前项和公式化简判断.
【详解】由,
可得,
又由,
则有,,
所以,,,
可得当时,,
故选:C.
二、填空题
13.已知圆与直线相切,则实数______.
【答案】0或
【分析】根据配方法,结合圆的切线性质、点到直线距离公式进行求解即可.
【详解】由,圆的圆心为,半径,∵圆和直线相切,∴或.
故答案为:0或
14.已知点,平面经过原点,且垂直于向量,则点到平面的距离为__________.
【答案】##
【分析】根据点到平面距离的向量求法求解即可.
【详解】由题意,,,故,所以点到平面的距离为.
故答案为:
15.在前n项和为的等差数列中,,,则______.
【答案】27
【分析】根据等差数列片段和的性质及等差中项列方程求.
【详解】由等差数列片段和性质:成等差数列,
所以,故.
故答案为:27
16.已知双曲线:(,),以原点为圆心,双曲线的焦距为半径的圆交轴于,两点,,是圆与双曲线在轴上方的两个交点.且,两点是的三等分点,则双曲线的离心率为______.
【答案】
【分析】根据已知条件作出图形,利用三角形的勾股定理及双曲线的定义,结合双曲线的离心率公式即可求解.
【详解】不妨设点在第二象限,双曲线的左、右焦点分别为,.如图所示,
∵,是的三等分点,∴,过点作轴的垂线,可得垂足为双曲线的右焦点.
在中,,
则在中,.
根据双曲线的定义可知,即,
所以双曲线的离心率为.
故答案为:.
三、解答题
17.已知数列满足,.
证明:数列是等比数列;
设,求数列的前n项和.
【答案】(1)详见解析;(2).
【分析】对数列的递推式两边加1,结合等比数列的定义,即可得证;
由对数的运算性质可得,再由裂项相消求和,化简可得所求和.
【详解】解:证明:数列满足,,
可得,
即有数列是首项为2,公比为3的等比数列;
由可得,
即有,
数列的前n项和.
【点睛】本题考查等比数列的定义、通项公式和数列的裂项相消求和,考查化简整理的运算能力,属于中档题.
18.已知圆的方程为.
(1)求实数的取值范围;
(2)若圆与直线交于M,N两点,且,求的值.
【答案】(1)
(2)
【分析】(1)将圆的一般方程用配方法化为标准方程,进而得到,解之即可;
(2)利用弦长公式求得,进而得到,易得的值.
【详解】(1)方程可化为,
∵此方程表示圆,
∴,即,即.
(2)由(1)可得圆心,半径,
则圆心到直线的距离为,
由弦长公式及,得,解得,
∴,得.
19.已知双曲线:(),直线与双曲线交于,两点.
(1)若点是双曲线的一个焦点,求双曲线的渐近线方程;
(2)若点的坐标为,直线的斜率等于1,且,求双曲线的离心率.
【答案】(1)
(2)
【分析】(1)利用双曲线的焦点坐标及标准方程,结合双曲线中三者的关系及双曲线的渐近线方程即可求解.
(2)根据已知条件及直线的点斜式方程,将联立双曲线方程与直线方程,利用韦达定理及点在直线上,结合两点间的距离公式及双曲线的离心率公式即可求解.
【详解】(1)∵点是双曲线的一个焦点,∴,
又∵且,解得,
∴双曲线的方程为,
∴双曲线的渐近线方程为;
(2)设直线的方程为且,
联立,可得,
则,∴,即,
∴
解得,即由可得,
故双曲线的离心率为.
20.如图,在三棱锥中,底面,,,,,,分别是上的三等分点,是的中点.
(1)证明:平面;
(2)求平面与平面的夹角的余弦值.
【答案】(1)证明见解析
(2)
【分析】(1)用余弦定理求出,从而得到,,建立空间直角坐标系,利用空间向量证明出线面垂直;
(2)求出平面的法向量,进而求出两平面的夹角余弦值.
【详解】(1)证明:,,,
根据余弦定理得,
所以,
所以,
以点为坐标原点,,所在直线为,轴,经过点垂直于,的直线为轴,建立空间直角坐标系,
则,,,,,,
,,,
,,
,
平面
(2),,,
设平面的一个法向量为,
由,所以
令,则,,
可得,
设平面的一个法向量,
由令,得,,
可得,
,
所以平面与平面夹角的余弦值为.
21.已知椭圆的长轴长为6,椭圆短轴的端点是,,且以为直径的圆经过点 .
(1)求椭圆C的方程;
(2)设过点M且斜率不为0的直线交椭圆C于两点.试问x轴上是否存在定点P,使PM平分 ?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)
(2)存在定点;
【分析】(1)根据题意确定的值,即可求得椭圆方程;
(2)设 ,直线 的方程为,联立方程可得根与系数的关系式,假设x轴上存在定点P,使平分,则可得 ,结合根与系数的关系化简,求得参数的值,可得结论.
【详解】(1)因为椭圆的长轴长为6,故,
椭圆短轴的端点是,,且以为直径的圆经过点,则,
所以椭圆C的方程是 ;
(2)设 ,直线的方程为,
将直线的方程与椭圆C的方程联立,
消去x得,因为M点在椭圆内,则必有,
所以,,
假设x轴上存在定点P,使平分,则直线的倾斜角互补,
所以 ,
设 ,则有 ,
将代入上式,整理得 ,
所以,
将 ,代入上式,整理得 ,
由于上式对任意实数m都成立,所以 ,
综上,存在定点 ,使平分 .
22.如图,已知抛物线:()上的点到焦点的距离的最小值为1,过点作抛物线的两条切线,切点分别为,,为线段上的动点,过点作抛物线的切线,切点为(异于点,),且直线交线段于点.
(1)求抛物线的方程;
(2)证明:为定值.
【答案】(1)
(2)证明见解析
【分析】(1)根据抛物线的性质即可求解;
(2)利用判别式求出切线的斜率,求出切点的坐标以及直线的方程,表示出,的坐标,即可证明为定值.
【详解】(1)抛物线:()的焦点坐标为,
因为此抛物线上到焦点距离最近的点就是坐标原点,
所以,,所以抛物线方程为;
(2)证明:设直线:,
由可得,
则,解得,
则,解得,
不妨令直线:,直线:,
则,,
设,,设直线:,
由可得,
由,
可得或(舍),
则,直线:.
由解得即,
故
为定值.
2023-2024学年河南省郑州市第四高级中学高二上学期期中数学试题含答案: 这是一份2023-2024学年河南省郑州市第四高级中学高二上学期期中数学试题含答案,共18页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
河南省郑州市第四高级中学2023-2024学年高二上学期期中数学试题(无答案): 这是一份河南省郑州市第四高级中学2023-2024学年高二上学期期中数学试题(无答案),共25页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年河南省郑州市高二上学期期末数学试题含解析: 这是一份2022-2023学年河南省郑州市高二上学期期末数学试题含解析,共15页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













