数学九年级上册25.5 相似三角形的性质教学ppt课件

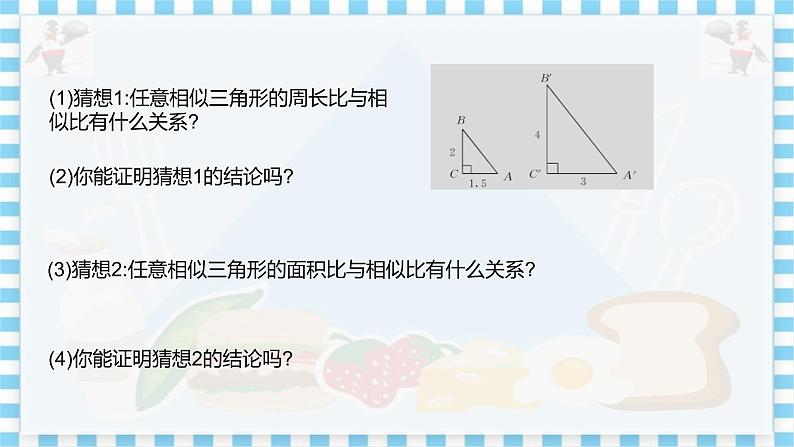
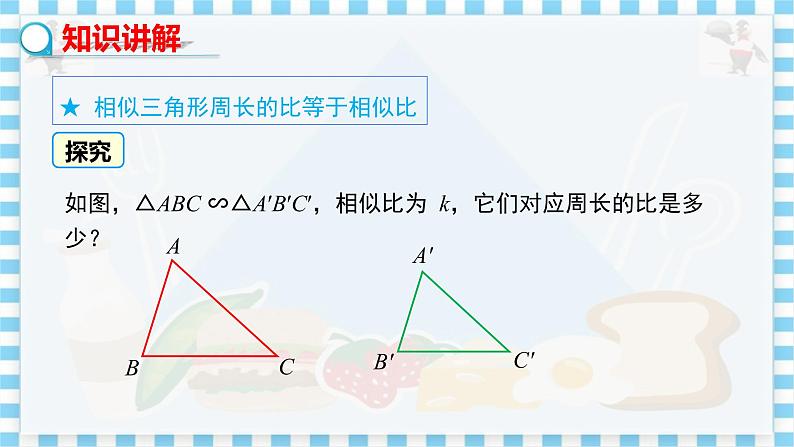
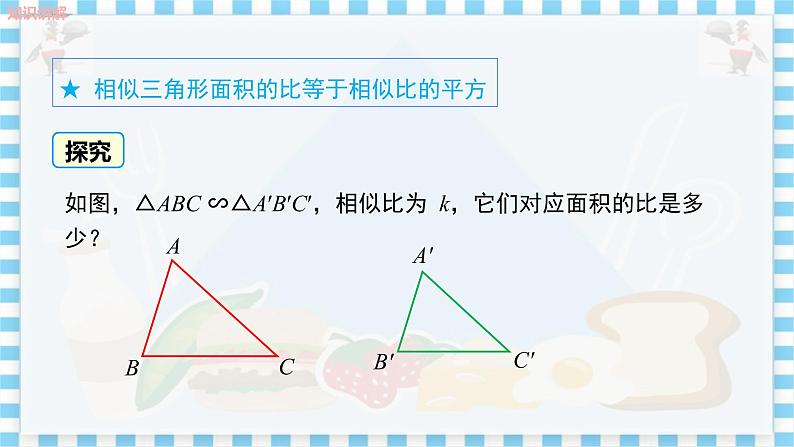
教学目标

1.知道相似三角形的周长比、面积比与相似比的关系.

2.会利用相似三角形的性质解决实际问题.

3.通过交流、归纳相似三角形的周长比、面积比与相似比的关系，体会知识迁移、温故知新的好处.

教学重难点

重点：相似三角形周长比、面积比与相似比的关系的推导.

难点：利用相似三角形周长比、面积比的关系解决实际问题.

教学过程

知识回顾

  师：相似三角形有哪些性质？

生1：相似三角形的对应角相等、对应边成比例.

生2：相似三角形对应高的比、对应中线的比、对应角平分线的比都

等于相似比.

师：相似三角形还有哪些性质呢？这节课继续研究.

设计意图：教师抛出问题，激发学生思考，从而调动学生学习的积极性，为下面的学习奠定基础.

探究新知

根据图上标出的数据，回答下列问题：

(1)根据图8中数据易知两个直角三角形相似，相似比是多少?

(2)计算这两个三角形的周长，它们的周长比与相似比有什么关系?

(3)计算两个三角形的面积，它们的面积比与相似比有什么关系?

猜想1:任意相似三角形的周长比与相似比有什么关系?

你能证明猜想1的结论吗?

猜想2:任意相似三角形的面积比与相似比有什么关系?

你能证明猜想2的结论吗?

如图9，△ ABC∽△A′B′C′，相似比为.

图9

师：写出图9中所有成比例的线段.

生：======.

师：△ABC与△A′B′C′的周长比是多少？怎么求？

生：∵ ===，

∴ ==.

由此得到△ABC与△A′B′C′的周长比是.

师：△ABC与△A′B′C′的面积比又是多少？与同伴交流.

生：∵ S△ABC=AB•CD，S△A′B′C′=A′B′•C′D′，

∴ S△ABC∶S△A′B′C′====.

师：如果△ABC∽△A′B′C′，相似比为其他数，那么△ABC与△A′B′C′的周长比和面积比分别是多少？

把全班同学分为8个小组，每一小组选一个数值作为相似比，计算周长比和面积比.

生：都得到周长比等于相似比，面积比等于相似比的平方.

师：如果△ABC∽△A′B′C′，相似比为k，你还能得到相同的结论吗？

找三位同学到黑板上板书解答过程.

学生总结，教师指导：得到相似三角形的周长比等于相似比，面积比等于相似比的平方.

设计意图：使学生建立从特殊到一般的思想，感受数学知识的严谨性.

典型例题

例1　已知△ABC与△A′B′C′中，∠C＝∠C′＝90°，∠A＝∠A′，BC＝6，AC＝8，

A′B′＝20，则△A′B′C′的周长为　　　　.

解析：在Rt△ABC中，斜边AB＝＝10，

∴ △ABC的周长＝6＋8＋10＝24.

又∵ ∠C＝∠C′ ＝90°，∠A＝∠A ′，∴ △ABC∽△A′B′C′.

∵ 两个相似三角形的周长比等于它们的相似比，

∴ .

∴ △A′B′C′的周长＝2×△ABC的周长＝48.

答案：48

例2　如图10所示，正方形DEFM 内接于△ ABC，若＝ 1，＝ 4，求.

解：过点A 作AQ ⊥ BC 交BC 于点Q，交DE 于点P.

∵  四边形DEFM 是正方形，

∴  DE ∥ BC，DE ＝ PQ，

∴  AP ⊥ DE，即AP是△ADE 的高.

∵ ＝4，∴ DE＝2.

∵ ＝1，∴  AP·DE＝1.

∴ AP＝1，∴ AQ＝ AP+PQ＝3.

∵  DE ∥ BC，∴ △ADE ∽△ABC，

∴ ，∴ ，

∴ BC＝6. ∴ ＝BC·AQ＝×6×3＝9.

课堂练习

1.在一张由复印机复印出来的纸上，一个三角形的一条边的长由原来的1 cm变成4 cm，那么它的周长由原来的3 cm变成(　　)

A.6 cm     B.12 cm

C.24 cm     D.48 cm

2.在△ABC中，点D、E分别在AB、AC上，∠AED=∠B，如果AE=2，△ADE的面积为4，四边形BCDE的面积为5，那么AB的长为________.

3.如图11所示，在等边三角形ABC中，点D，E分别在AB，AC边上，且DE∥BC，如果BC=6 cm，， 那么△ADE的周长等于　　　　cm，△ADE与四边形BCED的面积比为　　　　. 

图11                         图12                                 图13

4. 如图12，在△ABC 中，DE∥BC，EF∥AB，已知 △ADE 和△EFC 的面积分别为 4 和 9，求 △ABC 的面积.

   5.如图13，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E，H分别在AB，AC上.已知BC＝40 cm，AD＝30 cm .

（1）求证：△AEH∽△ABC；

（2）求这个正方形的边长与面积.

参考答案

1.B　2. 3   3.6  1:8

4.解：∵ DE∥BC，EF∥AB，

∴ △ADE∽△ABC，

∠ADE＝∠EFC，∠A＝∠CEF，

∴ △ADE∽△EFC.

又∵ ，

∴ AE∶FC＝2∶3，

则AE∶AC＝2∶5，

∴ ，∴ ＝25.

5.解：（1）∵ 四边形EFGH是正方形，∴ EH∥FG，即EH∥BC，

∴ △AEH∽△ABC.

（2）如图14，HE与AD交于点P，由（1）知AEH∽△ABC，

∴ .

∵ AD是BC边上的高，∴ PD＝EF.

又∵ 四边形EFGH是正方形，

∴ EF＝FG＝GH＝EH， ∴ AP＝AD－PD＝AD－EF＝AD－EH.

∴ ，解得EH＝（cm），

∴ .

∴ 这个正方形的边长为cm，面积为.

课堂小结

（学生总结，老师点评）

相似三角形周长、面积的性质.

布置作业

教材第87页练习第1，2题.

板书设计

25.5　相似三角形的性质

第2课时　相似三角形周长、面积的比

相似三角形的性质：

相似三角形的周长比等于相似比；

相似三角形的面积比等于相似比的平方.  

教学反思

教学反思

教学反思

教学反思