湘教版八年级上册3.1 平方根教学课件ppt

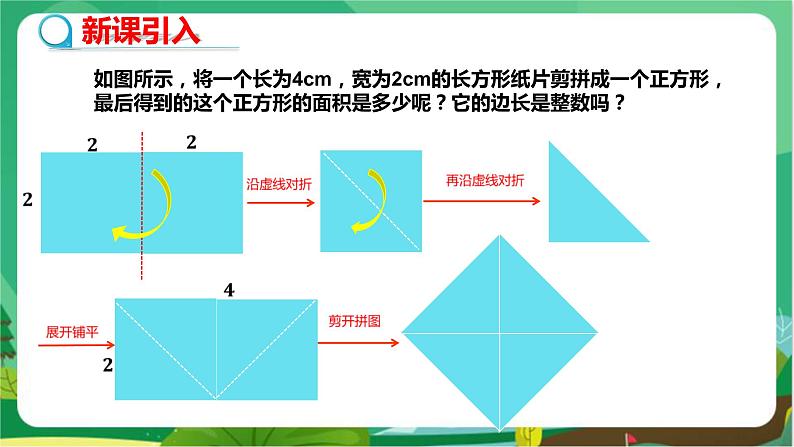
教学目标

1.认识无理数.

2.会用计算器计算一个正数的平方根.

教学重难点

重点: 无理数的概念.

难点：通过学习平方根，认识数学与生活的密切联系.

教学过程

导入新课

如图1所示，将一个长为4 cm，宽为2 cm的长方形纸片剪拼成一个正方形，最后得到的这个正方形的面积是多少呢？它的边长是整数吗？

图1

探究新知

（找学生回答上面的问题）

正方形的面积为8 cm2，由于22＝4，32＝9，而4<8<9，因此它的边长不是整数.

1.无理数

观察下列结果：

2.82＝7.84，              2.92＝8.41；

2.822＝7.952 4            2.832＝8.008 9

2.8282＝7.997 584         2.8292＝8.003 241

2.828 42＝7.999 846 56     2.828 52＝8.000 412 25

…                             …

从上述数据，你能猜出面积为8的正方形的边长是多少吗？

回答：面积为8的正方形，它的边长应该比2.828大，比2.829小，……

由此猜想，面积为8 cm2的正方形，它的边长是一个小数点后面的位数可以不断增加的小数，是一个无限不循环的小数.

我们知道，有理数包括整数和分数，整数和分数可统一写成分数的形式（整数可以看作分母为1的分数）.也就是说，有理数总可写成（m，n是整数，且m≠0）的形式.例如，

2＝＝2.0；＝0.5；.

任何整数、分数都可以化为有限小数或无限循环小数.

反过来，任何有限小数和无限循环小数都可以写成分数形式，因此有理数是有限小数或无限循环小数.

结论：面积为8的正方形，它的边长不是有理数.

我们把小数位数无限，且小数部分不循环的小数称为无限不循环小数.把无限不循环小数叫作无理数.

【问题】像这样的无限不循环小数还有哪些？

＝1.732 050 80…，π＝3.141 592 65…，这些数都是无限不循环小数.

归类： （1）根号型；（2）π型；（3）类似循环但不循环小数.

无理数与有理数一样，也有正负之分.例如：，，是正无理数，-，-，-是负无理数.    

2.近似数

根据实际需要，我们往往用一个有限小数来近似地表示一个无理数.

    例如：π＝3.141 592 6…，用四舍五入法，分别取到小数点后面第二位，第三位，…，得到π≈3.14， π≈3.142，…，我们称3.14，3.142是π的精确到小数点后面第二位，第三位的近似值.

3.14，3.142，3.1416，…都是π的近似值，称它们为近似数.

3.用计算器求算术平方根或近似值

例1　用计算器求的近似值（精确到小数点后面第三位）.

解：按键

显示：2.828 427 125

所以

【问题】利用计算器求平方根的按键顺序一般是什么？

回答：一般是先按根号键，再按被开方数，如果被开方数含有加法运算，需要加括号，最后按等号键.不同品牌的计算器，其使用方法可能不同.

课堂练习

1.在计算器上按键，下列计算结果正确的是（　　）

A.4.123　　　　B.-4.13　　　　C.-4　　　　D.4.13

2.估计在（　　）

A.3~4之间    B.4~5之间    C.5~6之间    D.6~7之间

3.设n为正整数，且n<<n+1，则n的值为（　　）

A.5           B.6          C.7           D.8

4.与最接近的整数是（　　）

A.7           B.8         C.9            D.10

参考答案

1.A   2.C   3.C  4.C

课堂小结

1.小数位数无限，且小数部分不循环的小数称为无限不循环小数.

2.无限不循环小数叫作无理数.

布置作业

课本第111页习题3.1第3，4，5，6题.

板书设计

教学反思

教学反思

教学反思