初中数学湘教版八年级上册第3章 实数3.1 平方根优秀ppt课件

课题名

无理数、用计算器求平方根

教学目标

知识与技能：理解掌握无理数的概念，能区分无理数和有理数，并能用计算器求一个无理数的近似值。

过程与方法：通过等积变形引出无理数，然后学习了无理数的概念、分类及表现形式，并用计算器求一个无理数的近似值。

情感态度：培养学生观察比较能力，分类思想，从实践中总结规律及解题技巧的能力。获得相关数学知识和技能，激发学生学习数学的兴趣。

教学重点

理解掌握无理数的概念，能区分无理数和有理数，并能用计算器求一个无理数的近似值

教学难点

能根据无理数的概念，区分无理数和有理数。

教学准备

教师准备：制作《无理数、用计算器求平方根》课件。

学生准备：预习课本第108～110页的《无理数、用计算器求平方根》。

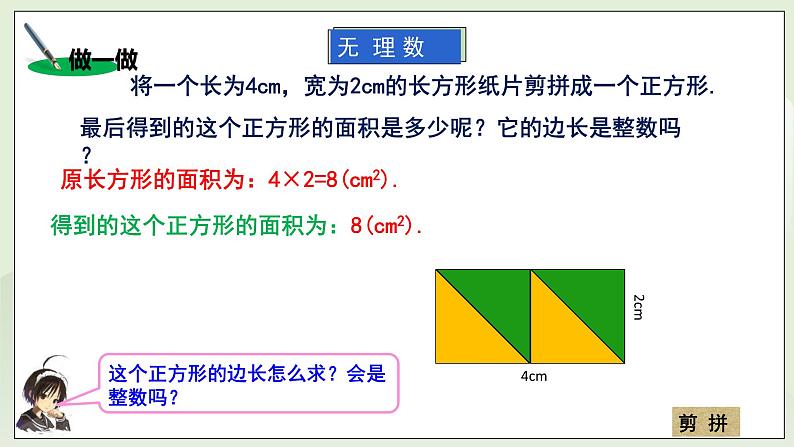
教学过程

一、温故知新     

1、填空：

1）、16的平方根是  4    。   2）、的平方根是  ±2   。

3）、的平方根是  ±  。 4）、的算术平方根是  2   。

5）、的算术平方根是    。

2、算一算：

1)、 -= -7=-

2)、 -+= -12+9=-

3）、× -×

=25× -6×

=1

二、情境导入

将一个长为4cm，宽为2cm的长方形纸片剪拼成一个正方形，最后得到的这个正方形的面积是多少呢？它的边长是整数吗？

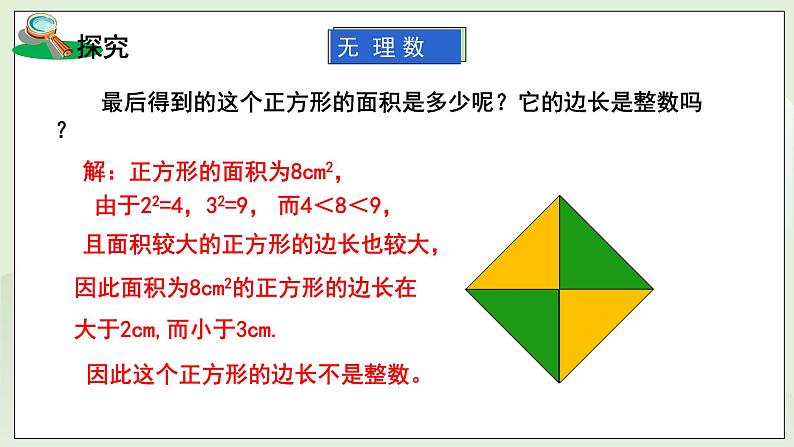
原长方形的面积为：4×2=8(cm2)，得到的这个正方形的面积为：4×2=8(cm2).

∵22=4，32=9，而4＜8＜9，且面积较大的正方形的边长也较大，

∴面积为8cm2的正方形的边长在大于2cm,而小于3cm.

∴这个正方形的边长不是整数。

三、新授内容

（活动一）：看一看，想一想

观察下列结果：

2.82=7.84，            2.92=8.41；

2.822=7.9524           2.832=8.0089

2.8282=7.997584        2.8292=8.003241

        …                          …

从上述数据，你能猜出面积为8的正方形的边长是多少吗？

答：面积为8的正方形，它的边长应该比2.828大，比2.829小，…

结论：面积为8cm2的正方形，它的边长是一个小数点后面的位数可以不断增加的小数.这个边长不是分数，从而它既不是有限小数，也不是无限循环小数，这种小数叫作无限不循环小数。

（活动二）：无理数

1、概念：无限不循环小数叫作无理数.

2、无理数的举例：

圆周率π=3.14159565……也是一个无理数;

=1.4142136…，-=-1.7320508…,是无理数;

3、无理数按正负分类：

①正无理数：，π，……

②负无理数：-，-π，…… 

4、无理数的表现形式：

①小数形式：无限不循环小数。如：π，7.151551555…，-1.010010001……。

②根式形式：开不尽方的根式。如：-，，。

③混合形式：化简后含有无限不循环小数或开不尽方的根式。如：，3-，-1.

5、对无理数的点三错误认识：

1、分数是无理数；2、无限小数是无理数；3、带根号的数都是无理数；

（活动三）：做一做——典例分析

例：下列数中:0，+3；-π，， ,0.101 001 0001..(每相邻两个1之间依次多一个0).其中无理数的个数为( C  )：

(A)1； (B)2；  (C)3；  (D)4。

§题析：无理数的表现形式：①、小数形式：无限不循环小数；

②根式形式：开不尽方的根式；③混合形式：化简后含有无限不循环小数或开不尽方的根式。

（活动四）：读一读，学一学

根据实际需要，我们往往用一个有限小数来近似地表示一个无理数.例如π=3.1415926…，用四舍五入法，分别取到小数点后面第二位，第三位，…，得到π=3.14，π=3.142，…，我们称3.14，3.142是π  的精确到小数点后面第二位，第三位的近似值.

3.14，3.142，3.141 6，…都是π的近似值，称它们为近似数。

§提示：取近似值一定要看到多一位止，然后根据四舍五入法取近似值。

（活动五）：做一做——一用计算器求平方根的值

例3  用计算器求下列各式的值。

1）

解：依次按键：，1，0，2，4，=,显示：32

∴=32.

2)  (精确到小数点后面第一位）

解：依次按键：，8，=,显示：2.828427125

∴≈2.8.     

四、课堂小测

1、下列各数: -2，0， ，0.020020002…每相邻两个2之间依次多一个)，π-3， ，其中无理数的个数是( C   )

(A)   4；    (B)  3；         (C) 2；      (D)1。

2、 用计算器求下列各式的值。

1)

解：依次按键：，3,1,3,6,=,显示：56

∴=56.

2)

解：依次按键：，1,·,5,3,7,6,=,显示：1.24

∴=1.24.   

3、 面各为6cm2的正方形，它的边长是多少？用计算器求边长的近似值（解：精确到0.001cm)

  解：≈2.449(cm)

答：答：它的边长约是2.449cm

4、用计算器分别求  ，， ，， 的近似值（精确到0.001）。

解：≈1.414； ≈1.732； ≈2.236；

≈3.317；   ≈0.762

布置作业

课作：P111  习题3.1 第4、5题

家作：P111  习题3.1 第6、9题并预习课本第112~114页。

板书设计

教学反思

本节课通过等积变形引出无理数，学习了无理数的分类及表现形式，并利用计算器求平方根的近似值。其中区分无理数与有理数是本节课的重点和难点。在教学中，要以实例为基础，分类讲解，让学生理解。