高中数学北师大版 (2019)选择性必修 第二册7.2 实际问题中的最值问题优秀ppt课件

这是一份高中数学北师大版 (2019)选择性必修 第二册7.2 实际问题中的最值问题优秀ppt课件，共23页。PPT课件主要包含了新知引入，新知讲解，二最优化问题等内容，欢迎下载使用。

1.了解实际问题中导数的意义.2.了解导数在解决最优化问题（利润最大、效率最高、用料最省等）中的作用.3.能利用导数求出某些实际问题的最大值(最小值)． 核心素养：数学运算、逻辑推理
在前面的学习中，我们知道，瞬时速度就是求解路程关于时间的函数式的某点处变化量，即求某点处的导数值，那么在其他实际问题中，导数具有怎样的意义呢？上节课我们还学习了导数与最值的关系，在一些实际问题中，常遇到求最值，如何利用导数工具去解决这些问题？
一 实际问题中导数的意义
在实际问题中，经常会遇到解决一些如面积最小、体积最大、成本最低、时间最少等问题，这些问题通称为最优化问题.
利用导数解决生活中的最优化问题的一般步骤1.分析实际问题中各量之间的关系.列出实际问题的数学模型,写出实际问题中变量之间的函数关系y=f(x),根据实际意义确定定义域.2.求函数y=f(x)的导数f'(x).解方程f'(x)=0得出定义域内的实根,确定极值点.3.比较函数在区间端点和极值点处的函数值,获得所求的最大(小)值.4.还原到原实际问题中作答.
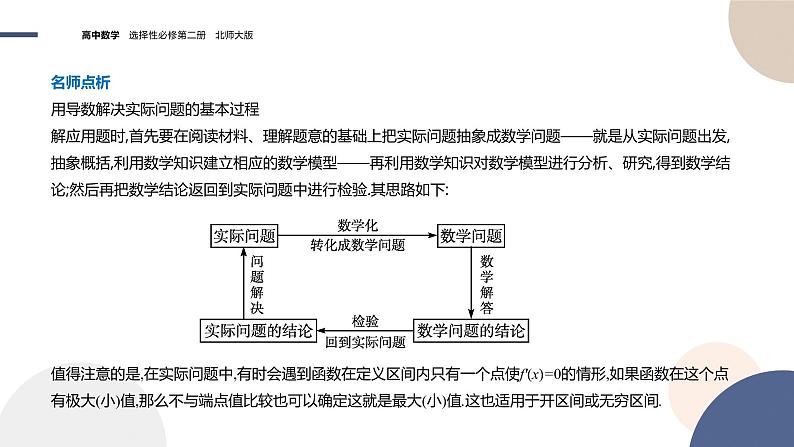
名师点析 用导数解决实际问题的基本过程解应用题时,首先要在阅读材料、理解题意的基础上把实际问题抽象成数学问题——就是从实际问题出发,抽象概括,利用数学知识建立相应的数学模型——再利用数学知识对数学模型进行分析、研究,得到数学结论;然后再把数学结论返回到实际问题中进行检验.其思路如下:
值得注意的是,在实际问题中,有时会遇到函数在定义区间内只有一个点使f'(x)=0的情形,如果函数在这个点有极大(小)值,那么不与端点值比较也可以确定这就是最大(小)值.这也适用于开区间或无穷区间.
一 利润最大、效率最高问题
分析 (1)根据x=5时,y=11求a的值.(2)把每日的利润表示为销售价格x的函数,用导数求最大值.
由上表可得,x=4是函数f(x)在区间(3,6)内的极大值点,也是最大值点,所以,当x=4时,函数f(x)取得最大值,且最大值等于42.故当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.
反思感悟利润最大问题的求解方法利用导数解决利润最大问题,关键是要建立利润的函数关系式,然后借助导数研究函数的最大值,注意函数定义域的限制以及实际意义.
二 费用最低、用料最省
反思感悟费用最低问题的求解策略(1)用料最省、成本(费用)最低问题是日常生活中常见的问题之一,解决这类问题要明确自变量的意义以及最值问题所研究的对象.正确书写函数表达式,准确求导,结合实际作答.(2)利用导数的方法解决实际问题,当在定义区间内只有一个点使f'(x)=0时,如果函数在这点有极大(小)值,那么不与端点值比较,也可以知道在这个点取得最大(小)值.
即时训练一艘轮船在航行中的燃料费和它的速度的立方成正比.已知速度为每小时10千米时,燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问轮船的速度是多少时,航行1千米所需的费用总和最少?
例3 用总长为14.8 m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5 m,那么高为多少时容器的容积最大,并求出它的最大容积.
三 面积、体积最大问题
分析 可设容器底面短边的长为x m,那么长边的长以及高就可用x表示出来,从而得到容积与x的函数关系式,然后用导数求得最大值.
反思感悟面积、体积最大问题的求解策略求面积、体积的最大值问题是生活、生产中的常见问题,解决这类问题的关键是根据题设确定出自变量及其取值范围,利用几何性质写出面积或体积关于自变量的函数,然后利用导数的方法来解.
即时训练周长为20 cm的矩形,绕一条边旋转成一个圆柱,则圆柱体积的最大值为　　　　　cm3. 
2.做一个容积为256 cm3的方底无盖水箱,要使用料最省,水箱的底面边长为(　　)A.5 cmB.6 cmC.7 cm D.8 cm
1.知识清单：（1）导数在实际问题中的意义.（2）用导数解决最优化问题.2. 方法技巧：在实际问题中,有时会遇到函数在定义区间内只有一个点使f'(x)=0的情形,如果函数在这个点有极大(小)值,那么不与端点值比较也可以确定这就是最大(小)值.
实际问题解决步骤(1)审题:阅读理解文字表达的题意,分清条件和结论,找出问题的主要关系.(2)建模:将文字语言转化成数学语言,利用数学知识建立相应的数学模型.(3)解模:把数学问题化归为常规问题,选择合适的数学方法求解.(4)对结果进行验证评估,定性、定量分析,作出正确的判断,确定其答案.