

山东省菏泽市鄄城县2022-2023学年九年级下学期第一次月考数学试题
展开
这是一份山东省菏泽市鄄城县2022-2023学年九年级下学期第一次月考数学试题,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022- -2023年度第二学期第一次月考九年级数学试题卷1 (选择题)一、选择题 (本题共计8小题 ,每题3分,共计24分)1.-l-2|的相反数是( )A.2 B. C.-2 D.-2.我国传统文化中的“福禄寿喜”图(如图)由四个图案构成,这四个图案中是中心对称图形的是( )A.B.C.D.
3.如图,已知AB∥FE,∠ABC=75°,∠CDE=130°,则∠BCD的值为( )A.80° B.40° C.30° D.25°
4. 如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P、Q分别为AO、AD的中点,则PQ的长度为( )A.10 B.5 C.2.5 D.2.255. 如图,AB为⊙O的直径,AB=4,弦CD=2,则劣弧的长为( )A. B. C.π D.2π6. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( )
A.60° B.70° C.75° D.85°
7. 下列运算正确的是( )A. B. C. D. 8. 如图,边长为2的正方形ABCD,点P从点A出发以每秒1个单位长度的速度沿A-D-C的路径向点C运动,同时点Q从点B出发以每秒2个单位长度的速度沿B-C-D-A的路径向点A运动,当Q到达终点时,P停止移动,设△PQC的面积为S,运动时间为t秒,则能大致反映S与t的函数关系的图象是( )
A.B.C.D.
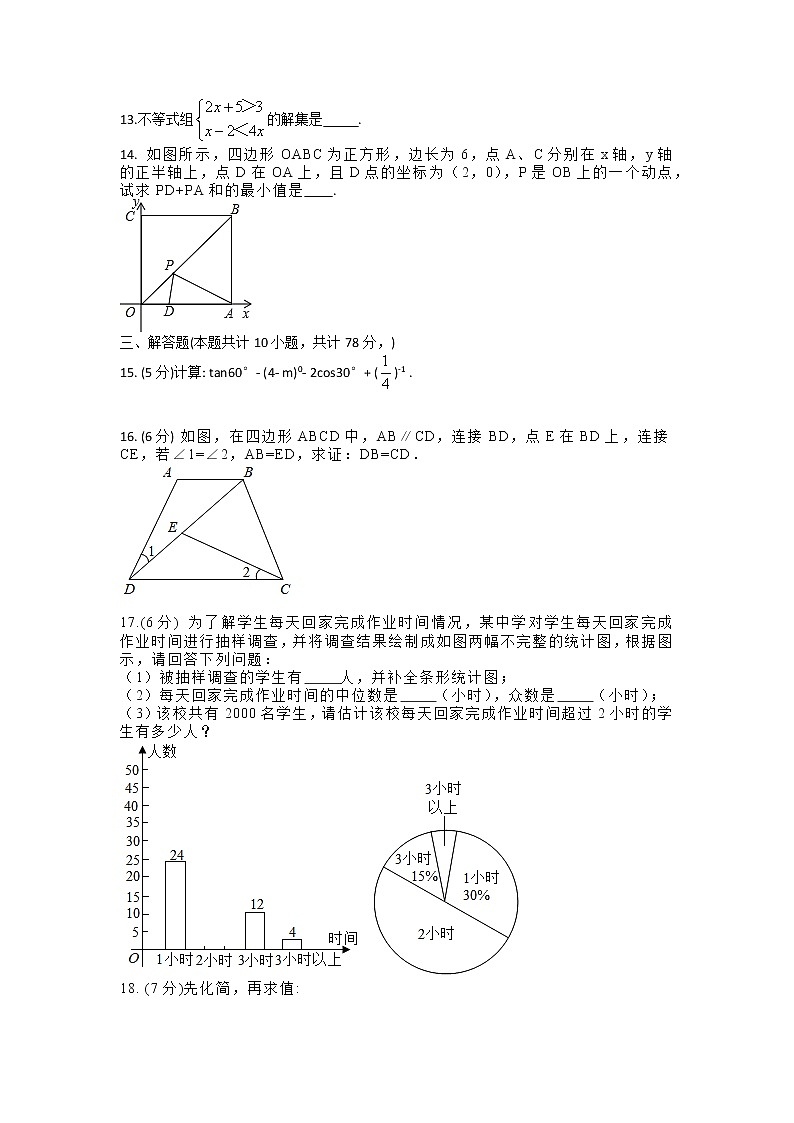
卷II (非选择题)二、填空题(本题共计6小题,每题3分,共计18分,)9.分解因式: x3-4x = .10.一个正多边形的一个内角是它相邻外角度数的3倍,则这是一个正 边形.11. 《九章算术》是中国古代《算经十书》最重要的一部,它的出现标志着中国古代数学形成了完整的体系,其中有一道阐述“盈不足数”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?意思是说:现有一些人共同买一个物品,每人出8元,还盈余3元:每人出7元,则还差4元,问共有多少人?这个物品的价格是多少?若设总共有x人,则可列方程为 .12.在平面直角坐标系xOy中,直线y = 3x与双曲线y= (k≠0)交于A,B两点,若点A坐标为(m,3),则点B的坐标为 .13.不等式组的解集是 .14. 如图所示,四边形OABC为正方形,边长为6,点A、C分别在x轴,y轴的正半轴上,点D在OA上,且D点的坐标为(2,0),P是OB上的一个动点,试求PD+PA和的最小值是 .三、解答题(本题共计10小题,共计78分,)15. (5分)计算: tan60°- (4- m)0- 2cos30°+ ()-1 . 16. (6分) 如图,在四边形ABCD中,AB∥CD,连接BD,点E在BD上,连接CE,若∠1=∠2,AB=ED,求证:DB=CD. 17.(6分) 为了解学生每天回家完成作业时间情况,某中学对学生每天回家完成作业时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
(1)被抽样调查的学生有 人,并补全条形统计图;
(2)每天回家完成作业时间的中位数是 (小时),众数是 (小时);
(3)该校共有2000名学生,请估计该校每天回家完成作业时间超过2小时的学生有多少人?18. (7分)先化简,再求值:, 其中a, b满足|a-3|+(b-2)2=0. 19. (7分) 如图,一艘货船由西向东行驶,在点B处测得灯塔A位于北偏东60°,航行16海里后到达点C处,测得灯塔A位于北偏东30°,货船不改变航向继续向东航行,求灯塔与货船的最短距离?(结果保留根号) 20. 蓝田樱桃果实大,细嫩多汁,甜酸适口,娇艳欲滴,馥郁甜香,极具地方特色.小张想在蓝田县某果园购买一些樱桃,经了解,现有甲、乙两家樱桃园的樱桃可供采摘,这两家樱桃的品质相同,定价均为每千克20元,但两家果园的采摘方案不同:
甲樱桃园:游客进园需购买32元的票,采摘的樱桃按定价的6折优惠;
乙樱桃园:不需要购买门票,采摘的樱桃按定价付款不优惠.
设小张采摘的樱桃数量为x千克,他在甲、乙果园采摘所需总费用分别为y甲、y乙元.
(1)分别求出y甲、y乙与x之间的函数关系式;
(2)小张应选择哪家樱桃园采摘樱桃更划算? 21.(8 分) 已知关于x的方程x2+2x+a-2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)当该方程的一个根为1时,求a的值及方程的另一根. 22.(9分) 如图,在平面直角坐标系xOy中,函数y= (x>0)的图象与直线y=x-2交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于x轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数y= (x>0)的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围. 23.(10分) 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,连接OD,过点D作⊙O的切线DE,交AC于点E,延长CA交⊙O于点F,连接BF.
(1)求证:DE⊥AC;
(2)若⊙O的直径为5,cosC=,求CF的长.24.(12分) 如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=-x2+4x刻画,斜坡可以用一次函数y= x刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标. 参考答案1.A 2. B 3.D 4.C 5.C 6.C 7.A 8.C 9. 10.8 11. 8x-3=7x+4 12.(-1,-3) 13. 14. 15. tan60°- (4- m)0- 2cos30°+ ()-1=-1-+4=316. ∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
∴DB=CD.17. (1)24÷30%=80(人),
完成时间在“3小时以上”的所占的百分比为4÷80=5%,
完成时间在“2小时”的所占的百分比为1-5%-30%-15%=50%,
完成时间在“2小时”的人数为80×50%=40(人),补全条形统计图如图所示:
(2)这80名学生完成作业时间出现次数最多的是“2小时”,共出现40次,因此众数是2小时,
将这80名学生完成作业时间从小到大排列后处在中间位置的两个数都是2小时,因此中位数是2小时,
故答案为:2,2;
(3)2000×(15%+5%)=400(人),
答:该校2000名学生中每天回家完成作业时间超过2小时的有400人.18. 原式= ∵|a-3|+(b-2)2=0,
∴a-3=0,b-2=0,即a=3,b=2,
则原式=1.19. 过点A作AD⊥BC,垂足为D.如图所示:
根据题意可知∠ABC=90°-60°=30°,∠ACD=90°-30°=60°,
∵∠ACD=∠ABC+∠BAC,
∴∠BAC=30°=∠ABC,
∴CA=CB=16海里,
在Rt△ACD中,∠ADC=90°,∠ACD=60°,sin∠ACD=,
∴sin60°=,
∴AD=16×sin60°=16×=8(海里);
即灯塔与货船的最短距离为8海里.20. (1)由题意,得:y甲=32+20×0.6x=12x+32,
y乙=20x.
(2)当y甲<y乙,即12x+32<20x,解得x>4,
所以当采摘量大于4千克时,到甲樱桃园更划算;
当y甲=y乙,即12x+32=20x,解得x=4,
所以当采摘量为4千克时,到两家樱桃园所需总费用一样;
当y甲>y乙,即12x+32>20x,解得x<4,
所以当采摘量小于4千克时,到乙樱桃园更划算.21. (1)∵b2-4ac=(2)2-4×1×(a-2)=12-4a>0,
解得:a<3.
∴a的取值范围是a<3;(2)设方程的另一根为x1,由根与系数的关系得:,解得:,
则a的值是-1,该方程的另一根为-3. 22. (1)将A(3,m)代入y=x-2,
∴m=3-2=1,
∴A(3,1),
将A(3,1)代入y= ,
∴k=3×1=3,
(2)①PM=PN,证明如下:
当n=1时,P(1,1),
令y=1,代入y=x-2,
x-2=1,
∴x=3,
∴M(3,1),
∴PM=2,
令x=1代入y=,
∴y=3,
∴N(1,3),
∴PN=2
∴PM=PN,
②P(n,n),n>0
点P在直线y=x上,
∴M(n+2,n),
∴PM=2,
∵PN≥PM,
即PN≥2,
∵PN=|-n|,
|−n|≥2
∴0<n≤1或n≥323. (1)证明:∵DE为⊙O的切线,
∴OD⊥DE,
∵AB=AC,
∴∠ABC=∠C,
∵OB=OD,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴DE⊥AC;
(2)解:连接AD,
∵AB为⊙O的直径,
∴∠BDA=90°,
∵AB=5,
∴AC=AB=5,
在Rt△ADC中,cosC=,
∴CD=4,
在Rt△CED中,cosC= ,
∴CE=,
∵AB=AC,AD⊥BC,
∴BD=DC,
∵AB为⊙O的直径,
∴∠BFA=90°,
∵DE⊥AC,
∴DE∥BF,
∴EF=CE=,
∴CF=.24. (1)由题意得,y=-x2+4x=-(x-2)2+4,
故二次函数图象的最高点P的坐标为(2,4);
(2)联立两解析式可得:,
解得:,或.
故可得点A的坐标为(,);
(3)如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.
S△POA=S△POQ+S梯形PQBA-S△BOA
=×2×4+×(+4)×(-2)-××
=;
(4)过P作OA的平行线,交抛物线于点M,连接OM、AM,则△MOA的面积等于△POA的面积.
设直线PM的解析式为y=x+b,
∵P的坐标为(2,4),
∴4=×2+b,解得b=3,
∴直线PM的解析式为y=x+3.
由,解得(舍去),,
∴点M的坐标为(,).
相关试卷
这是一份山东省菏泽市鄄城县2022-2023学年八年级下学期期中数学试题,共8页。试卷主要包含了下列说法错误的是,已知命题等内容,欢迎下载使用。
这是一份山东省菏泽市鄄城县2023-2024学年九年级上学期期中数学试题,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份山东省菏泽市鄄城县2022-2023学年八年级下学期7月期末数学试题,共3页。









