

中考经典几何模型与最值问题 专题06 对角互补模型在三角形中应用
展开专题06 对角互补模型在三角形中应用
【专题说明】
对角互补模型证明全等三角形,其辅助线的添加非常灵活,尤其是很多全等证明的题目经常和旋转综合考察,作为初二数学中的压轴题型。我们集中讲解旋转综合中常见的模型、题型,希望各位同学能从中收益。
【知识总结】
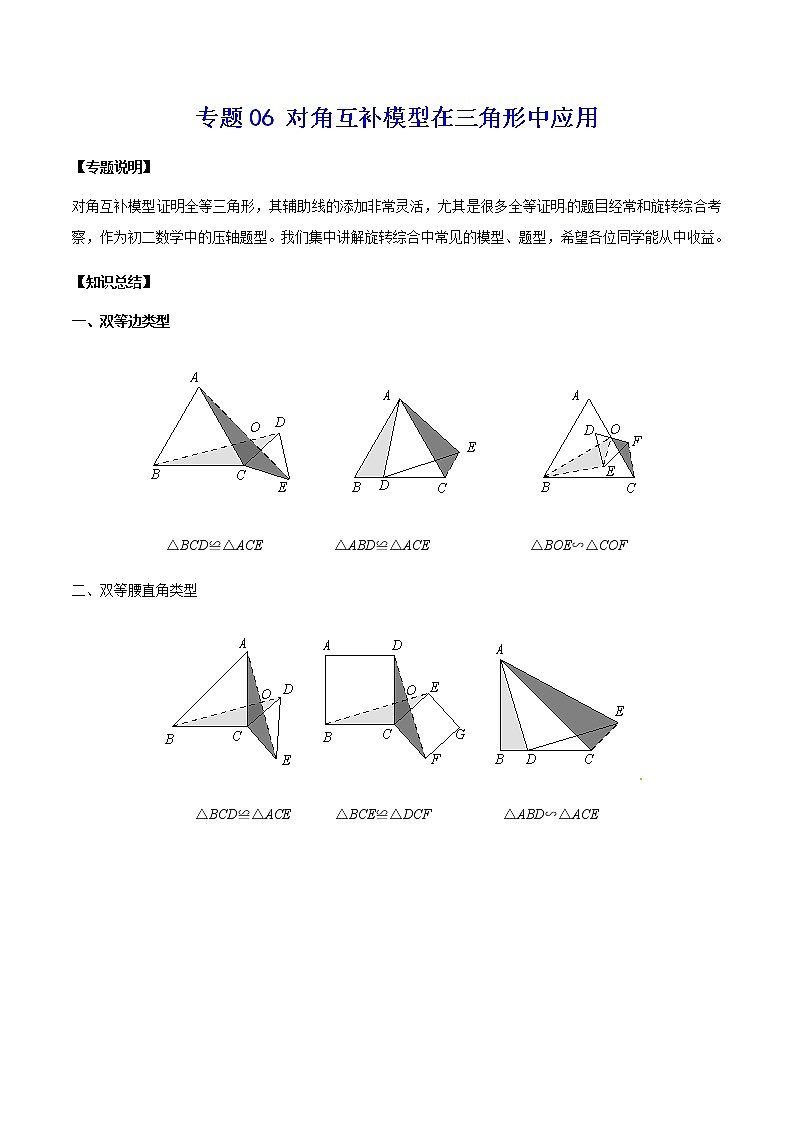
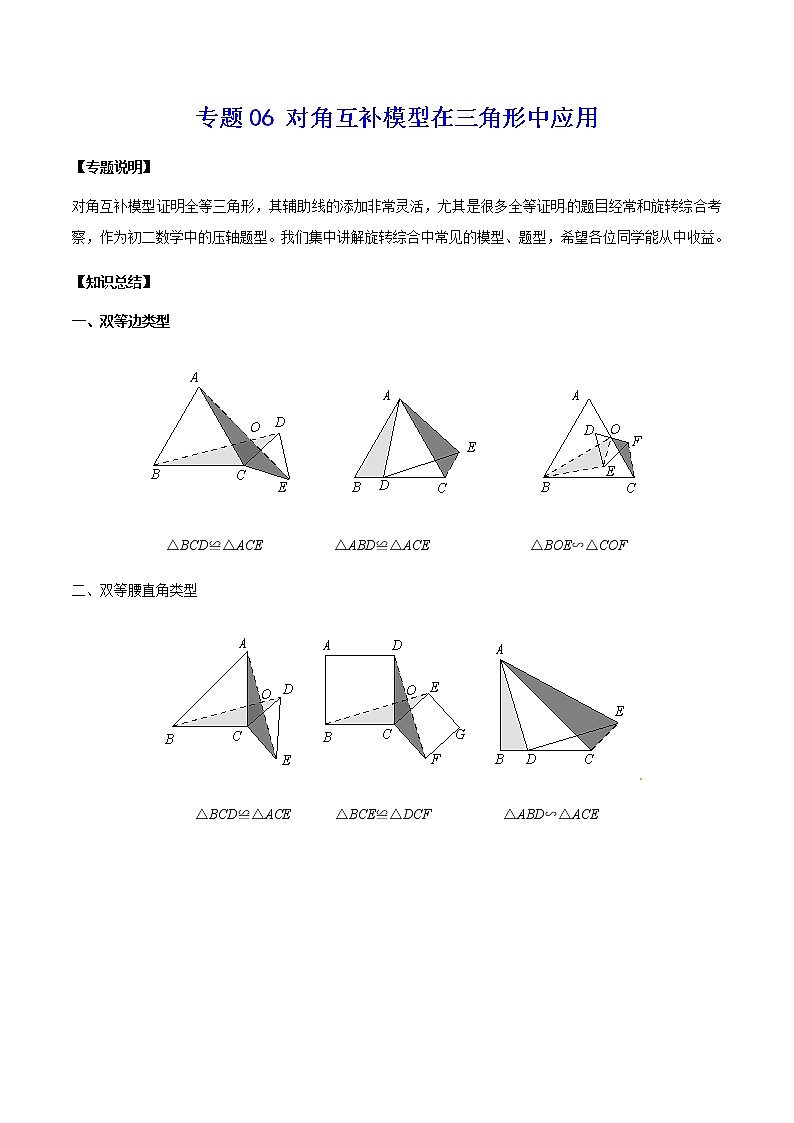
一、双等边类型
△BCD≌△ACE △ABD≌△ACE △BOE∽△COF
二、双等腰直角类型
△BCD≌△ACE △BCE≌△DCF △ABD∽△ACE
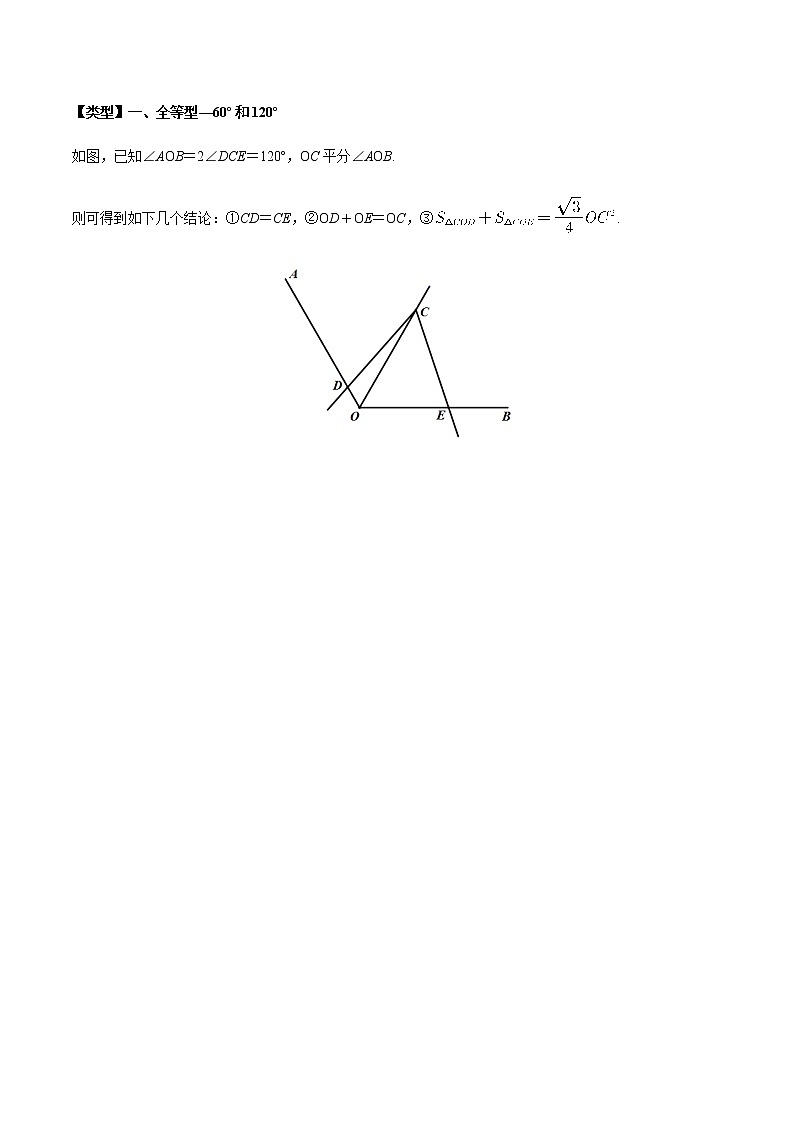
【类型】一、全等型 —60º和120º
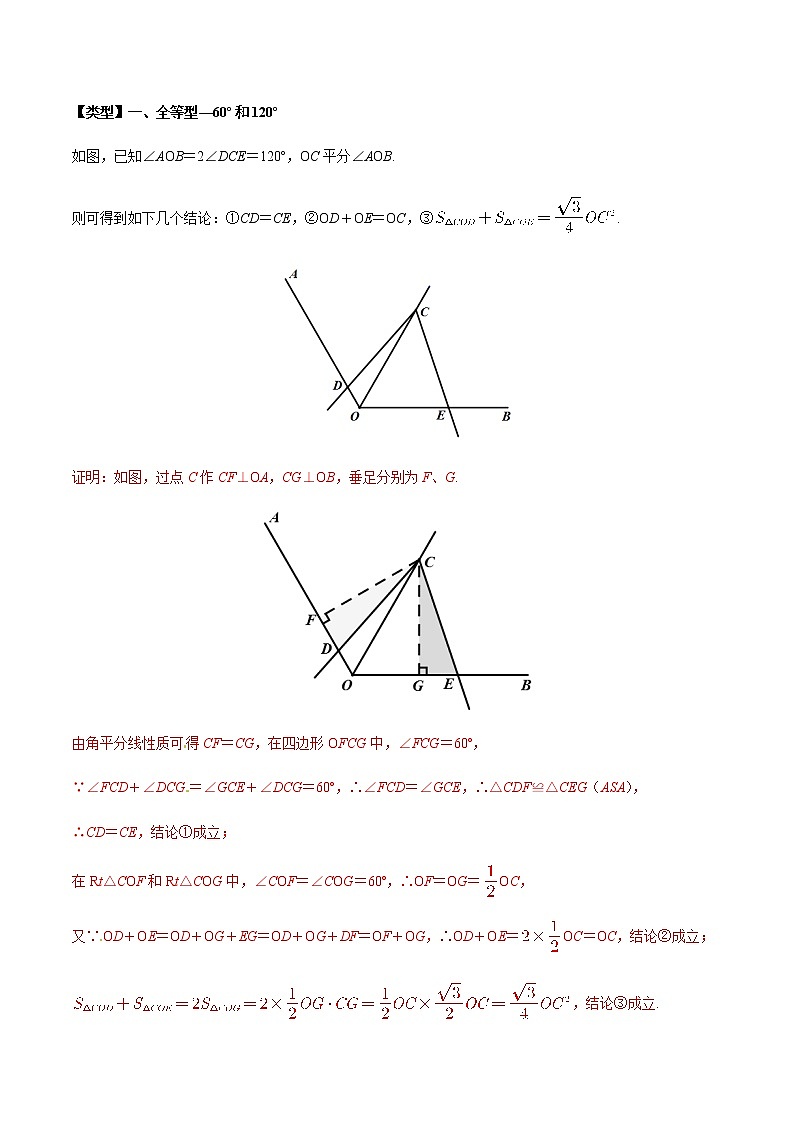
如图,已知∠AOB=2∠DCE=120º,OC平分∠AOB.
则可得到如下几个结论:①CD=CE,②OD+OE=OC,③.
证明:如图,过点C作CF⊥OA,CG⊥OB,垂足分别为F、G.
由角平分线性质可得CF=CG,在四边形OFCG中,∠FCG=60º,
∵∠FCD+∠DCG=∠GCE+∠DCG=60º,∴∠FCD=∠GCE,∴△CDF≌△CEG(ASA),
∴CD=CE,结论①成立;
在Rt△COF和Rt△COG中,∠COF=∠COG=60º,∴OF=OG=OC,
又∵OD+OE=OD+OG+EG=OD+OG+DF=OF+OG,∴OD+OE=OC=OC,结论②成立;
,结论③成立.
【类型】二、全等型—90º
如图,已知∠AOB=∠DCE=90º,OC平分∠AOB.
则可以得到如下几个结论:①CD=CE,②OD+OE=OC,③.
证明:如图,过点C作CM⊥OA于点M,CN⊥OB于点N.
∵OC平分∠AOB,∴CM=CN(角平分线上的点到角两边的距离相等)
在正方形MONC中,由题意可得∠MCN=360º-∠CMO-∠AOB-∠CNO=90º,∴∠MCD+∠DCN=90º,
又∵∠DCE=90º,∴∠ECN+∠MCD=90º,∴∠MCD=∠ECN
∴△CDM≌△CEN,∴CD=CE,∴结论①成立;
∵四边形MONC为正方形,∴OM=ON=OC,
又∵OD+OE=OD+ON+NE=OD+ON+DM=OM+ON,∴OD+OE=OC,∴结论②成立;
∴,∴结论③成立.
如图,已知∠DCE的一边与AO的延长线交于点D,∠AOB=∠DCE=90º,OC平分∠AOB
则可得到如下几个结论:①CD=CE,②OE-OD=OC,③.
证明:如图,过点C作CF⊥OA,CG⊥OB,垂足分别为F、G.
由角平分线性质可得CF=CG,∴四边形CFOG为正方形,
∵∠1+∠2=90º,∠3+∠2=90º,∴∠1=∠3,∴△CDF≌△CEG,
∴CD=CE,结论①成立;
在正方形CFOG中,OF=OG=OC,
∵OE-OD=OG+GE-OD=OG+FD-OD=OG+OF,∴OE-OD=OC=OC,②成立;
【类型】三、全等型—和
如图,已知∠AOB=,∠DCE=,OC平分∠AOB.
则可以得到以下结论:①CD=CE,②OD+OE=2OC·cos,③.
证明:如图,过点C作CF⊥OA,CG⊥OB,垂足分别为F、G.
[
证△CDF≌△CEG可得CD=CE,结论①成立,
在Rt△COF和Rt△COG中,∠COF=∠COG=,∴OF=OG=OC·,
又∵OD+OE=OD+OG+EG=OD+OG+DF=OF+OG,∴OD+OE=2OC·cos,结论②成立,
,结论③成立.
【类型】四、相似型—90º
如图,已知∠AOB=∠DCE=90º,∠BOC=.
结论:CE=CD·.
证明【方法一】:如图1,过点C作CF⊥OA,CG⊥OB,垂足分别为F、G.
先证△CEG∽△CDF,即,又∵四边形CFOG是矩形,∴CF=DG,
在Rt△COG中,,∴CE=CD·;
证明【方法二】:如图2,过点C作CF⊥OC交OB于点F.
通过证明△CFE∽△COD可得.
【基础训练】
【类型】一、一般情况
基本条件:△ABC∽△EDC,连接AE、BD后,有△AEC∽△BDC,相似比为AC边与BC边之比。
可见,上面几种有图形中有全等情况出现,只因图形中有边长相等。
1、(直接用双子)如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
(1)△OBC与△ABD全等吗?判断并证明你的结论;
(2)着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标;若有变化,说明理由.
[
解析:①全等.理由:∵△AOB和△CBD是等边三角形,
∴OB=AB,∠OBA=∠OAB=60°,BC=BD,∠CBD=60°,
∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD,
在△OBC和△ABD中,∵,∴△OBC≌△ABD(SAS).
②不变.理由:∵△OBC≌△ABD,∴∠BAD=∠BOC=60°,
又∵∠OAB=60°,∴∠OAE=180°﹣∠OAB﹣∠BAD=60°,
∴Rt△OEA中,AE=2OA=2,∴OE=,
∴点E的位置不会发生变化,E的坐标为E(0,).
2、如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )
A. B. C.1 D.
解析:设Q是AB的中点,连接DQ,
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
∵AB=AC=2,O为AC中点,∴AQ=AO,
在△AQD和△AOE中,,∴△AQD≌△AOE(SAS),
∴QD=OE,
∵点D在直线BC上运动,∴当QD⊥BC时,QD最小,
∵△ABC是等腰直角三角形,∴∠B=45°
∵QD⊥BC,∴△QBD是等腰直角三角形
∴QD=QB,
∵QB=AB=1,
∴QD=,
∴线段OE的最小值是为.
故选:B.
3、如图1,在Rt△ABC中,∠B=90°,cosC=,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为θ.当0°≤θ<360°时的大小有无变化?请仅就图2的情况给出证明.
(图1) (图2)
解析:当0°≤α<360°时,的大小没有变化,∵∠ECD=∠ACB,∴∠ECA=∠DCB,
又∵==,∴△ECA∽△DCB,∴==;
【类型】二、旋转构造双子型
此类图的特点在于图形的不完整。一且补全图形,答案即可解出,而方法不仅仅是构造,亦可用旋转,构造与旋转本就可互相代替,但我们常常选用旋转来解决!不过本专题打算用构造的思路去解决!面转的方法读者可自行尝试,图是一样的!
1.如图所示,在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD的长为_________.
解析:作AD′⊥AD,AD′=AD,连接CD′,DD′,如图:
∵∠BAC+∠CAD=∠DAD′+∠CAD,即∠BAD=∠CAD′,
在△BAD与△CAD′中,,∴△BAD≌△CAD′(SAS),
∴BD=CD′,∠DAD′=90°,
由勾股定理得DD′==3,∠D′DA+∠ADC=90°,
由勾股定理得CD′==,∴BD=CD′=.
2、如图,在△ABC中,∠ABC=60°,AB==8,以AC为腰,点A为顶点作等腰△ACD,且∠DAC=120°,则BD的长为________.
解析:以A为旋转中心,把△BAC逆时针旋转120°,得到△EAD,连接BE,作AP⊥BE于P,
则∠BAE=120°,AB=AE,∴∠ABE=∠AEB=30°,
∴BP=AB•cos∠ABP=3,∠AEB=90°,∴BE=2BP=6,
在Rt△BED中,BD==10,
【巩固提升】
1、如图所示,已知△ABC和△BDE均为等边三角形,连接AD、CE,若∠BAD=39°,那么∠ACE=_______.
解析:∵△ABC和△BDE均为等边三角形,∴∠ABC=∠DBE=60°,AB=BC,BE=BD,
∴∠CBD=60°,∴∠ABD=∠CBE=120°
在△ABD和△CBE中,,∴△ABD≌△CBE,(SAS),∴∠AEC=∠ADB,
∵∠ADB=180°﹣∠ABD﹣∠BAD=21°,∴∠AEC=21°,∴∠ACE=99°
2、如图,△ABC为等边三角形,AB=2,点D为BC边上的动点,连接AD,以AD为一边向右作等边△ADE,连接CE
(1)在点D从点B运动到点C的过程中,点E运动的路径长为_________;
2)在点D的运动过程中,是否存在∠DEC=60°,若存在,求出BD的长,若不存在,请说明理由.
(3)取AC中点P,连接PE,在点D的运动过程中,求PE的最小值.
解析:
(1)△ABD≌△ACE可得BD=CE,E的运动路径的长即D的运动路径长,BC=2.
(2)∠DEC=60°相当于∠AEC=∠ADB=120°,即∠EDC=0°,此时点D与点B重合.因此不存在.
(3)∠ACE=60°,当PE⊥CE时取最小值.PE=PC×cos60°=.
3、在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到.
(1)如图1,当点在线段CA的延长线上时,求的度数;
(2)如图2,连接.若的面积为4,求的面积;
图1 图2
解析:(1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,
∴∠CC1B=∠C1CB=45°,
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°.
(2)∵△ABC≌△A1BC1,
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
∴∠ABA1=∠CBC1,
∴△ABA1∽△CBC1.
∴,
∵S△ABA1=4,
∴S△CBC1=;
4、【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:BM=CN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论BM=CN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,AB=6,AC=4,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究BM与CN的数量关系,并说明理由.
图1 图2 图3
(1)证明:∵△ABC、△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,∴∠BAM=∠CAN,
∵在△BAM和△CAN中,,∴△BAM≌△CAN(SAS),∴∠ABC=∠ACN.
(2)解:结论∠ABC=∠ACN仍成立;理由如下:∵△ABC、△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,∴∠BAM=∠CAN,
∵在△BAM和△CAN中,,∴△BAM≌△CAN(SAS),∴∠ABC=∠ACN.
(3)∠ABC=∠ACN;
理由如下:∵BA=BC,MA=MN,顶角∠ABC=∠AMN,
∴底角∠BAC=∠MAN,∴△ABC∽△AMN,∴=,
又∵∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,
∴∠BAM=∠CAN,∴△BAM∽△CAN,∴∠ABC=∠ACN.
5、如图,正方形ABCD、BGFE边长分别为2、1,正方形BGFE绕点B旋转,直线AE、GC相交于点H.
(1)在正方形BGFE绕点B旋转过程中,∠AHC的大小是否始终为90°,请说明理由;
(2)连接DH、BH,在正方形BGFE绕点B旋转过程中,求DH的最大值;
备用图
解析:(1)是,理由如下:
如图,由旋转知,∠ABE=CBG,
在正方形ABCD,BGFE中,
AB=BC,BE=BG,∠ADC=∠BCD=∠BAD=∠ABC=90°,
∴△ABE≌△CBG,
∴∠BAE=∠BCG,
记AH与BC的交点为点P,
∵∠APB=∠CPH,∠ABC+∠BAE+∠APB=180°
∠AHC+∠BCG+∠CPH=180°,
∴∠AHC=∠ABC=90°,
(2)DH≤DE+EG=BD=
6、如图1,已知点A(0,-3)和x轴上的动点C(m,0),△AOB和△BCD都是等边三角形.
(1)在C点运动的过程中,始终有两点的距离等于OC的长度,请将它找出来,并说明理由.
(2)如图2,将△BCD沿CD翻折得△ECD,当点C在x轴上运动时,设点E(x,y),请你用m来表示点E的坐标并求出点E运动时所在图象的解析式.
(3)在C点运动的过程中,当时,直接写出△ABD是等腰三角形时E点的坐标.
图1 图2
解析:(1)连接AD,如图1所示.
A、D两点间的距离始终等于OC的长度.理由如下:
∵△AOB和△BCD都是等边三角形,
∴AB=OB,BD=BC,∠ABO=∠CBD=60°,
∵∠ABD=∠ABO+∠OBD,∠OBC=∠OBD+∠DBC,
∴∠ABD=∠OBC.
在△ABD和△OBC中,有,
∴△ABD≌△OBC(SAS),
∴AD=OC.
(2)过D作DF⊥y轴于F,连接BE,如图2所示.
由(1)可知△ABD≌△OBC,
∴AD=OC=m,∠DAF=∠BAO﹣∠BAD=60°﹣(90°﹣60°)=30°
∴DF=AD•sin∠DAF=m,AF=AD•cos∠DAF=m,
∵A(0,﹣3),∴D(m,m﹣3).
∵将△BCD沿CD翻折得△ECD且△BCD是等边三角形,
∴四边形BCED是菱形,∴BE、CD互相平分.
∵△AOB是等边三角形,且点O(0,0),点A(0,﹣3),
∴点B(,﹣),∴E(m﹣,m﹣).
∵m﹣=(m﹣),∴点E在图形y=x上运动.
(3)∵点A(0,﹣3),点B(,﹣),点D(m,m﹣3),
∴AB=3,AD=m,BD==,
△ABD为等腰三角形分三种情况:
①当AB=AD时,有3=m,此时点E的坐标为(﹣,﹣);
②当AB=BD时,有3=,解得:m=0(舍去),或m=3,此时点E的坐标为(3,3);
③当AD=BD时,有m=,解得:m=(舍去).
综上:在C点运动过程中,当m>时,△ABD是等腰三角形时E点的坐标为(﹣,﹣)或(3,3).
7、【问题探究】
(1)如图1,锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,四边形ABCD中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45°,求BD的长.
(3)如图3,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.
图1 图2 图3
解析:(1)BD=CE.
理由是:∵∠BAE=∠CAD,
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,,∴△EAC≌△BAD,∴BD=CE;
(2)如图2,在△ABC的外部,以A为直角顶点作等腰直角△BAE,使∠BAE=90°,AE=AB,连接EA、EB、EC.
∵∠ACD=∠ADC=45°,
∴AC=AD,∠CAD=90°,
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,,∴△EAC≌△BAD,∴BD=CE.
∵AE=AB=7,
∴BE==7,∠ABE=∠AEB=45°,
又∵∠ABC=45°,
∴∠ABC+∠ABE=45°+45°=90°,
∴EC===,
∴BD=CE=.
(3)如图3,在线段AC的右侧过点A作AE⊥AB于点A,交BC的延长线于点E,连接BE.
∵AE⊥AB,
∴∠BAE=90°,
又∵∠ABC=45°,
∴∠E=∠ABC=45°,
∴AE=AB=7,BE==7,
又∵∠ACD=∠ADC=45°,
∴∠BAE=∠DAC=90°,
∴∠BAE﹣∠BAC=∠DAC﹣∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,,∴△EAC≌△BAD,∴BD=CE,
∵BC=3,
∴BD=CE=(7﹣3)cm.
2、(1)如图1,已知△ABC,以AB、AC为边分别向△ABC外作等边△ABD和等边△ACE,连接BE、CD,请你完成图形(尺规作图,不写作法,保留作图痕迹),并证明:BE=CD;
(2)如图2,利用(1)中的方法解决如下问题:在四边形ABCD中,AD=3,BD=2,∠ABC=∠ACB=∠ADB=45°,求BD的长;
(3)如图3,四边形ABCD中,∠BAC=90°,∠ADB=∠ABC=α,tanα==5,AD=12,求BD的长.
图1 图2 图3
解析:(1)如图1,分别以点A、B为圆心,以AB为半径画弧,交于点D,连接AD、BD,再分别以A、C为圆心,以AC为半径画弧,交于点E,连接AE、CE,则△ABD、△ACE就是所求作的等边三角形;
证明:如图1,∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠EAC=60°,∴∠DAC=∠BAE,
∴△DAC≌△BAE(SAS),
∴BE=CD;
(2)如图2,过A作AE⊥AD,使AD=AE=3,连接DE、CE,
由勾股定理得:DE==3,∴∠EDA=45°,
∵∠ADC=45°,∴∠EDC=∠EDA+∠ADC=90°,
∵∠ACB=∠ABC=45°,∴∠CAB=90°,
∴∠CAB+∠DAC=∠EAD+∠DAC,即∠EAC=∠DAB,
∵AE=AD,AC=AB,
∴△DAB≌△EAC(SAS),∴EC=BD,
在Rt△DCE中,EC===,
∴BD=EC=
(3)如图3,作直角三角形DAE,使得∠DAE=90°,
∠DEA=∠ACB,连接EC,
容易得到△DAE∽△BAC,∴,即,
∵∠DAE=∠BAC=90°,
∴∠DAE+∠DAC=∠BAC+∠DAC,即∠EAC=∠DAB,
∴△EAC∽△DAB,∴,
在△DCE中,∠ADC=∠ACB,∠EDA=∠ABC,∴∠EDC=90°,
∵,AD=12,
∴AE=9,∠DAE=90°,
∴DE==15,CE==5,
由△EAC∽△DAB,∴,BD=.
中考经典几何模型与最值问题 专题23 二次函数在实际应用中的最值问题试卷: 这是一份中考经典几何模型与最值问题 专题23 二次函数在实际应用中的最值问题试卷,文件包含专题23二次函数在实际应用中的最值问题教师版docx、专题23二次函数在实际应用中的最值问题学生版docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。
中考经典几何模型与最值问题 专题14 胡不归中的双线段模型与最值问题试卷: 这是一份中考经典几何模型与最值问题 专题14 胡不归中的双线段模型与最值问题试卷,文件包含专题14胡不归中的双线段模型与最值问题教师版docx、专题14胡不归中的双线段模型与最值问题学生版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
中考经典几何模型与最值问题 专题13 将军饮马模型与最值问题试卷: 这是一份中考经典几何模型与最值问题 专题13 将军饮马模型与最值问题试卷,文件包含专题13将军饮马模型与最值问题教师版docx、专题13将军饮马模型与最值问题学生版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。












