数学八年级下册19.2.3一次函数与方程、不等式第2课时教案设计

这是一份数学八年级下册19.2.3一次函数与方程、不等式第2课时教案设计，共9页。
八年级第十一讲“用函数的观点看方程（组）与不等式” .（第二课时）
[教学目标]:
知识技能：
1、熟练掌握一元一次不等式与一次函数的关系，会运用不等式解决函数有关问题；
2、通过具体问题初步体会一次函数的变化与一元一次不等式解集的联系；
3、感知不等式、函数、方程的不同作用与内在联系，并渗透“数学结合”思想.
数学思考：
1、经历不等式与函数问题的探讨过程，学习用联系的观点看待数学问题的辩证思想；
2、在教学过程中，学生体会数学中的比较和转化思想.
问题解决：
1、通过观察函数图象解决不等式解集问题，培养学生的观察能力、分析能力、归纳总结能力．
2、在与他人合作和交流过程中，能较好地理解他人的思考方法和结论。
情感态度：
学生在小组合作学习中体验学习的快乐，合作交流的好氛围，让学生更有机会体验自己与他人的想法，从而掌握知识，发展技能，获得愉快的心里体验.
[教学重点和难点]:
重点：初步建立“数”（一元一次不等式、方程）与“形”（一次函数之间的关系），根据一次函数的图象求一元一次不等式的解集（方程的解）
难点：理解一元一次不等式、方程与一次函数之间的关系及实际运用
[教学准备]:
动画多媒体语音课件
第二课时
教学过程：
教学路径

方案说明
一、课前谈话
上节课，我们学习了一次函数与方程、不等式组的关系，那么现在我们就来探讨一下一次函数与方程、不等式组的关系综合应用问题及实际问题中的应用！
二、自主探究，合作交流
初步性问题
探究类型之三 一次函数、方程（组）、不等式（组）与几何等知识的综合
例4 已知一次函数y=kx+b的图象经过点（-1，-5），且与函数y=x+1的图象相交于点A（，a）．
（1）求a的值；
（2）求不等式组0＜kx+b＜x+1的正整数解；
解析：（1）将点A的坐标代入y＝x+1求出a的值；（下一步）
（2）把（-1，-5）和（，a）的坐标分别代入y=kx+b，求出k和b的值，然后解不等式组.
答案：
解：
（1）把（，a）的坐标代入y=x+1，得a=.
（2）由（1）知A（，），
将（，），（-1，-5）的坐标分别代入y=kx+b中，
得解得
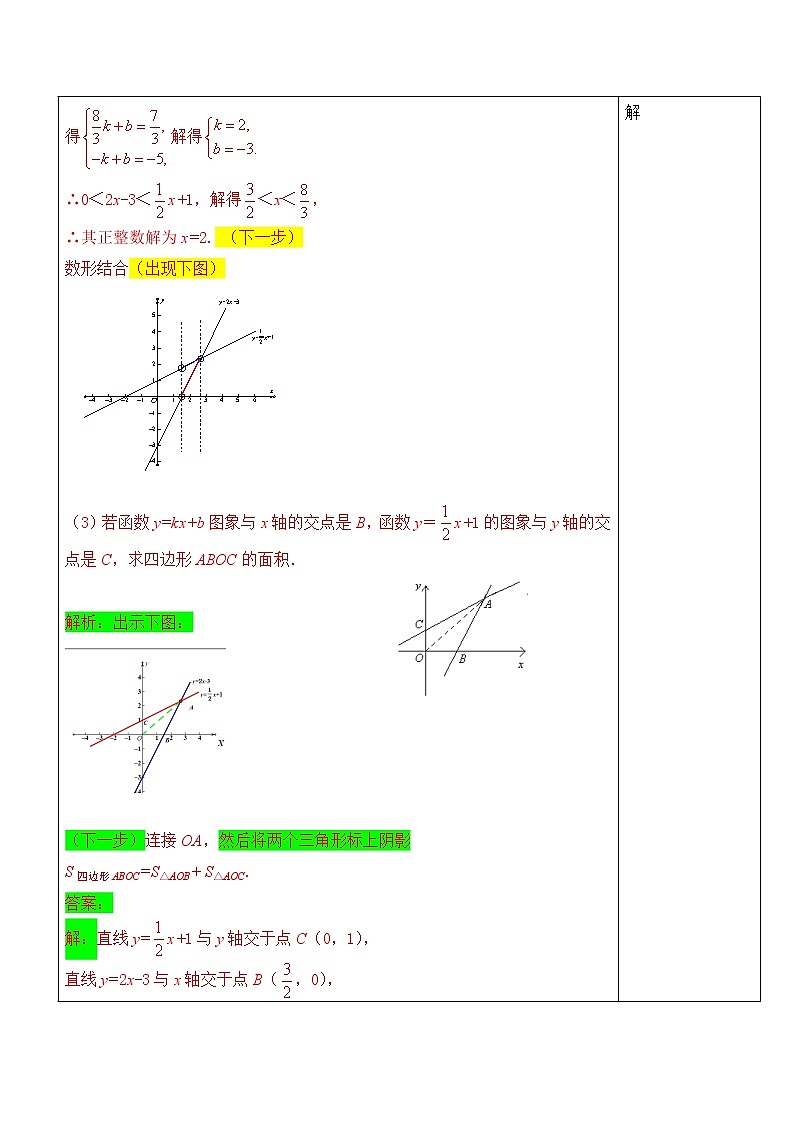
∴0＜2x-3＜x+1，解得＜x＜，
∴其正整数解为x=2. （下一步）
数形结合（出现下图）
（3）若函数y=kx+b图象与x轴的交点是B，函数y＝x+1的图象与y轴的交点是C，求四边形ABOC的面积．
解析：出示下图：
（下一步）连接OA，然后将两个三角形标上阴影
S四边形ABOC=S△AOB+ S△AOC.
答案：
解：直线y=x+1与y轴交于点C（0，1），
直线y=2x-3与x轴交于点B（，0），
连接OA,过点A分别作x轴，y轴的垂线，垂足分别为E,F,如图
（动画在图中作出）.
∴AE=,AF=.
∴S四边形ABOC=S△AOB+S△AOC=××+×1×=.
师：如何求a的值？
生：根据点在直线上将含有字母的坐标代入解析式.
师：如何求正整数解？
生：直接解不等式组求正整数解.
师：注意借助数形结合帮助理解题目，如何求三角形的面积？
生：利用面积的割补法求解.
师：数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化.
例5 如图，A（0，1），M（3，2），N（4，4）．动点P从点A出发，沿y轴以每秒1个单位的速度向上移动，且过点P的直线l：y=-x+b也随之移动，设移动时间为t秒．（分两道题出示）
（1）当t=3时，求直线l的解析式；
（2）若点M，N位于l的异侧，确定t的取值范围；
（3）直接写出t为何值时，点M关于l的对称点落在坐标轴上．
师：如何求直线l的解析式？
生：必须要先求出点P的坐标，点P的坐标为（0,1+t），当t=3时，点P（0,4）,将点P的坐标代入y=-x+b.
师：如何确定t的取值范围？
生：数形结合，分别求直线y=-x+b过点M,N时t的值.
师：如何求t值使得对称点在坐标轴上？（师重点给学生讲解）
生：数形结合，借助图形确定对称点的位置.
解析：点P的坐标为（0,1+t），代入y=-x+b可得b=1+t，故y=-x+1+t；
（下一步）
（1）直接把t=3代入即可；（下一步）
（2）出示动画（下一步）
分别把点M，N的坐标代入求出对应的t值，从而确定t的取值范围.
（3）点M（3,2）关于直线y=-x+1+t对称的点的坐标为（t-1，t-2）.
（下一步）
出示动画
答案：
解：易知点P的坐标为（0,1+t），代入y=-x+b可得b=1+t，故y=-x+1+t.
（1）当t=3时， y=-x+4．
（2）把（3,2）的坐标代入y=-x+1+t，得2=-3+1+t，即t=4，
此时直线l经过点M；
把（4,4）的坐标代入y=-x+1+t，得4=-4+1+t，即t=7，此时直线l经过点N；
所以当4＜t＜7时，点M，N位于l的异侧.
（3）点M（3,2）关于直线y=-x+1+t对称的点的坐标为（t-1，t-2）.
当t-1=0，即t=1时，落在y轴上；
当t-2=0，即t=2时，落在x轴上．
类似性问题
5. 如图，一次函数y=-x+2的图象分别与x轴、y轴交于点A、B，以线段AB为边在第一象限内作等腰Rt△ABC，∠BAC=
90°．求过B、C两点直线的解析式．
师：我们要怎么求直线的解析式呢？
生：先要求出点B,C的坐标
师：点B的坐标好求，那我们怎么求点C的坐标呢？
生：过点C作x轴的垂线，证三角形全等.
解析：
过点C作CD⊥x轴于点D（动画用手在图中作出），
（下一步）先求出点A，B的坐标，然后证明△AOB≌△CDA（同时将两个三角形填充颜色）得到AD=OB，CD=OA，从而确定出点C的坐标.
（下一步）设过点B，C的直线的解析式为y=kx+b，然后用待定系数法求k，b的值.
探究类型之四 实际问题中的一次函数与方程（组）的关系的运用
例 6 某中学九年级甲、乙两班商定举行一次远足活动，A、B两地相距10千米，甲班从A地出发匀速步行到B地，乙班从B地出发匀速步行到A地，两班同时出发，相向而行，设步行时间为x小时，甲、乙两班离A地的距离分别为千米、千米，、与x的函数关系图象如图所示，根据图象解答下列问题：
（1）直接写出、与x的函数关系式；
（2）求甲、乙两班学生出发后，几小时相遇？相遇时乙班离A地多少千米？
（3）甲、乙两班首次相距4千米时所用时间是多少小时？
师：如何求函数解析式？
生：待定系数法.
师：还有别的方法吗？
生：根据实际意义确定速度和距离.
师：如何求相遇的时间？
生：根据函数因变量的实际意义知=.
师：如何求首次相距4千米时的时间？
生：根据线段图知此时满足-=4.
师：求两个一次函数图象的交点坐标就是解由这两个函数解析式组成的二元一次方程组，方程组的解即为两个函数图象的交点坐标.
（1）解析1： 是关于x的正比例函数，是关于x的一次函数，用待定系数法求解；（下一步）
解析2：
甲离A地的距离y1 = 甲行驶的路程 = v甲·x（下一步）
乙离A地的距离y2 = AB两地的距离-乙行驶的路程 = 10-v乙·x
（2）解析：动画出示描图中的交点，然后出示：相遇时满足=；
（3）解析：首次相距4千米，即-=4. （下一步）
答案：
（1）解：=4x(0≤x≤2.5), =-5x+10(0≤x≤2).
（2）解：根据题意可知：两班相遇时，甲、乙离A地的距离相等，即=.由此可得一元一次方程-5x+10=4x,解这个方程，得x=.
当x=时，=-5×+10＝（千米）.
答：甲、乙两班学生出发后，时相遇，相遇时乙班离A地千米.
（3）解：根据题意，得-=4，即-5x+10-4x=4，
解这个方程，得x=.
答：甲、乙两班首次相距4千米所用时间是时.

类似性问题
4.我国青海省玉树地区发生强烈地震以后，国家立即启动救灾预案，积极展开向灾区运送救灾物资和对伤员的救治工作.已知西宁机场和玉树机场相距800千米，甲、乙两机沿同一航线各自从西宁、玉树出发，相向而行，如图，线段AB、CD分别表示甲、乙两机离玉树机场的距离s（百千米）和所用去的时间t（时）之间的函数关系的图象（注：为了方便计算，将平面直角坐标系中距离s的单位定为百千米.观察图象回答下列问题：
（1）乙机在甲机出发后几时，才从玉树机场出发？甲、乙两机的飞行速度每时各为多少千米？
（2）求甲、乙两机各自的s与t的函数关系式；
（3）甲、乙两机相遇时，乙机飞行了几时？离西宁机场多少千米？
学生独立完成，指定学生讲解.
三、课堂小结：
通过今天课的学习，你都收获了哪些知识呢？相信大家对不等式、函数、方程都有了一定的了解和掌握。希望你们在以后的学习中遇到类似的问题能迎刃而解、收获更多。
小组讨论
尝试解答
老师进行详细的讲解
找学生读题