北师大版高中数学必修第二册5-1-2复数的几何意义学案

4.1.2　复数的几何意义

1.复平面

建立直角坐标系来表示复数的平面叫做复平面．x轴叫做________，y轴叫做________，实轴上的点都表示__________；除________外，虚轴上的点都表示纯虚数．

2.复数的几何意义

(1)复数z＝a＋bi(a，b∈R) 复平面内的点__________；

(2)复数z＝a＋bi(a，b∈R) 平面向量________________．

3.复数的模

复数z＝a＋bi(a，b∈R)对应的向量为，则的模叫做复数z的模，记作|z|或|a＋bi|，且|z|＝________.

[点睛]　实轴、虚轴上的点与复数的对应关系

实轴上的点都表示实数；除了原点外，虚轴上的点都表示纯虚数，原点对应的有序实数对为(0,0)，它所确定的复数是z＝0＋0i＝0，表示的是实数.

4.共轭复数

若两个复数的实部相等，而虚部互为相反数，则称这两个复数互为共轭复数．复数z的共轭复数用表示．当z＝a＋bi(a，b∈R)时，＝a－bi.

注意：对共轭复数模的两点说明

(1)在复平面内，表示两个共轭复数的点关于实轴对称，并且它们的模相等；

(2)任意一个实数的共轭复数仍是它本身．

答案：1.实轴　虚轴　实数　原点

2.(1)Z(a，b)　(2)O＝(a，b)

3.

研习1   　复数与复平面内的点一一对应　　　　　　　　　　　　　　　　　　

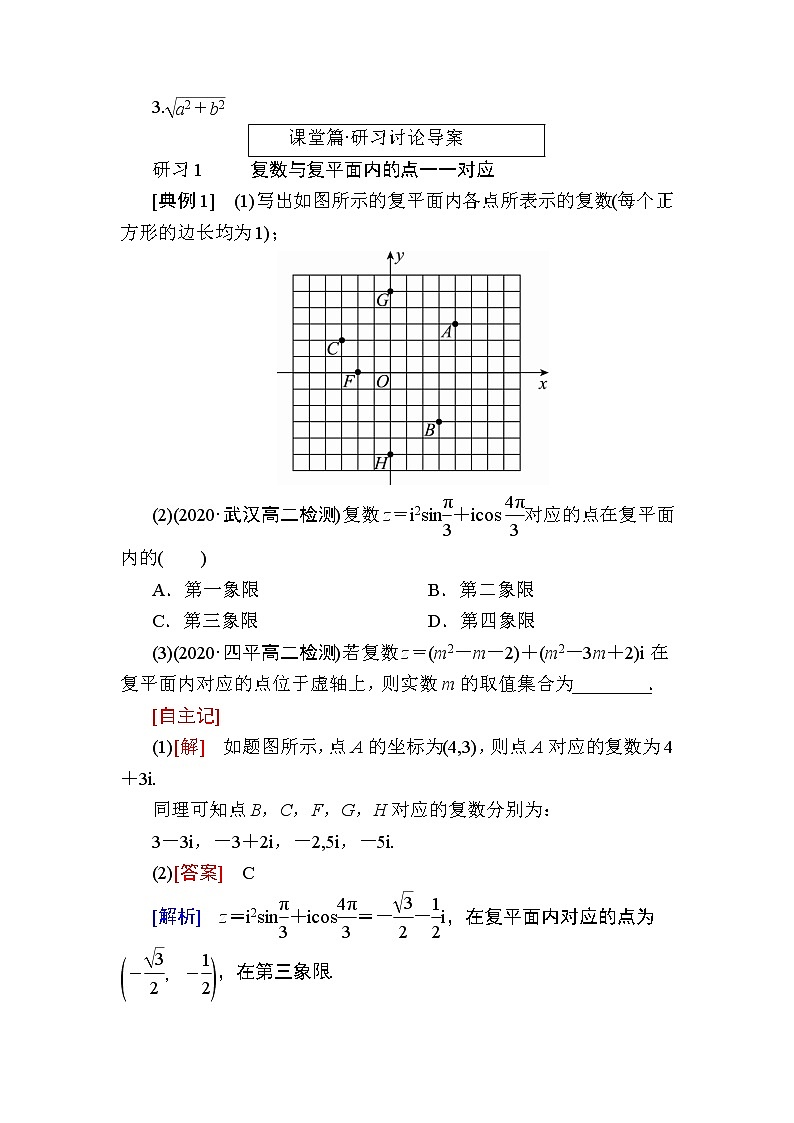
[典例1]　(1)写出如图所示的复平面内各点所表示的复数(每个正方形的边长均为1)；

(2)(2020·武汉高二检测)复数z＝i2sin＋icos对应的点在复平面内的(　　)

A．第一象限　　　　　　 B．第二象限

C．第三象限    D．第四象限

(3)(2020·四平高二检测)若复数z＝(m2－m－2)＋(m2－3m＋2)i在复平面内对应的点位于虚轴上，则实数m的取值集合为________．

[自主记]　

(1)[解]　如题图所示，点A的坐标为(4,3)，则点A对应的复数为4＋3i.

同理可知点B，C，F，G，H对应的复数分别为：

3－3i，－3＋2i，－2,5i，－5i.

(2)[答案]　C

[解析]　z＝i2sin＋icos＝－－i，在复平面内对应的点为，在第三象限.

(3)[答案]　{－1,2}

[解析]　因为复数z＝(m2－m－2)＋(m2－3m＋2)i在复平面内对应的点位于虚轴上，所以m2－m－2＝0，解得m＝2或m＝－1.

[巧归纳]　利用复数与点的对应解题的步骤

(1)找对应关系：复数的几何表示法即复数z＝a＋bi(a，b∈R)可以用复平面内的点Z(a，b)来表示，是解决此类问题的根据．

(2)列出方程(组)或不等式(组)：此类问题可寻求复数的实部与虚部应满足的条件，通过解方程(组)或不等式(组)求解.

[练习1]　在复平面内，若复数z＝(m2－m－2)＋(m2－3m＋2)i对应点(1)在虚轴上；(2)在第二象限；(3)在直线y＝x上，分别求实数m的取值范围．

解：复数z＝(m2－m－2)＋(m2－3m＋2)i的实部为m2－m－2，虚部为m2－3m＋2.

(1)由题意得m2－m－2＝0，解得m＝2或m＝－1.

(2)由题意得∴

∴－1<m<1.

(3)由已知得m2－m－2＝m2－3m＋2.∴m＝2.

研习2  复数与平面向量的对应关系

[典例2]　(1)已知平面直角坐标系中O是原点，向量，对应的复数分别为2－3i，－3＋2i，那么向量对应的复数是(　　)

A．－5＋5i    B．5－5i

C．5＋5i    D．－5－5i

(2)在复平面内，A，B，C三点对应的复数分别为1，2＋i，－1＋2i.

①求向量A，A，B对应的复数；

②判定△ABC的形状．

[自主记]　

(1)[答案]　B

[解析]　向量，对应的复数分别记作z1＝2－3i，z2＝－3＋2i，根据复数与复平面内的点一一对应，可得向量＝(2，－3)，＝(－3,2)．

由向量减法的坐标运算可得向量＝－＝(2＋3，－3－2)＝(5，－5)，根据复数与复平面内的点一一对应，可得向量对应的复数是5－5i.

(2)[解]　①由复数的几何意义知：

O＝(1,0)，O＝(2,1)，O＝(－1,2)，

∴A＝O－O＝(1,1)，

A＝O－O＝(－2,2)，

B＝O－O＝(－3,1)，

∴A，A，B对应的复数分别为1＋i，－2＋2i，－3＋i.

②∵|A|＝，|A|＝2，|B|＝，

∴|A|2＋|A|2＝|B|2，

∴△ABC是以BC为斜边的直角三角形.

[巧归纳]　复数与平面向量的对应关系

(1)根据复数与平面向量的对应关系，可知当平面向量的起点在原点时，向量的终点对应的复数即为向量对应的复数．反之复数对应的点确定后，从原点引出的指向该点的有向线段，即为复数对应的向量．

(2)解决复数与平面向量一一对应的问题时，一般以复数与复平面内的点一一对应为工具，实现复数、复平面内的点、向量之间的转化．

[练习2]　复数z1＝3＋4i，z2＝0，z3＝c＋(2c－6)i(c∈R)在复平面内对应的向量分别是，，，若·<0，求c的取值范围．

解：由条件知Z1(3,4)，Z2(0,0)，Z3(c,2c－6)，

所以＝(－3，－4)，＝(c－3,2c－10)．

又·＝－3(c－3)＋(－4)×(2c－10)

＝49－11c<0，

解得c>，所以c的取值范围是.

研习3  复数的模及其应用

[典例3]　已知复数z1＝＋i，z2＝－＋i.

(1)求|z1|及|z2|并比较大小；

(2)设z∈C，满足条件|z2|≤|z|≤|z1|的点Z的轨迹是什么图形？

[自主记]　

[解]　(1)|z1|＝|＋i|＝＝2，

|z2|＝＝1.

∴|z1|>|z2|.

(2)由|z2|≤|z|≤|z1|及(1)知1≤|z|≤2.

因为|z|的几何意义就是复数z对应的点到原点的距离，所以|z|≥1表示|z|＝1所表示的圆及其外部所有点组成的集合，|z|≤2表示|z|＝2所表示的圆及其内部所有点组成的集合．故符合题设条件点的集合是以O为圆心，以1和2为半径的两圆之间的圆环(包含圆周)，如图所示．

[巧归纳]　几种常用图形的复数方程

(1)线段的垂直平分线．

A(x1，y1)对应复数z1，B(x2，y2)对应复数z2，线段AB的垂直平分线的复数方程为|z－z1|＝|z－z2|.

(2)圆．

圆心为P(a，b)，半径为r(r>0)的圆的复数方程为|z－z0|＝r(其中圆心P对应复数z0)．特别地，当圆心为坐标原点时，圆的复数方程为|z|＝r.

(3)椭圆．

以2a为长轴长，坐标原点为中心且焦点在坐标轴上的椭圆的复数方程为|z－z1|＋|z－z2|＝2a(其中椭圆的两个焦点F1和F2分别对应复数z1和z2)．

(4)双曲线．

以2a为实轴长，坐标原点为中心且焦点在坐标轴上的双曲线的复数方程为|z－z1|－|z－z2|＝±2a(其中双曲线的两个焦点F1和F2分别对应复数z1和z2).

[练习3]　若复数z满足|z＋＋i|≤1，求|z|的最大值和最小值．

解：因为|z＋＋i|＝1，即|z－(－－i)|＝1，故复数z对应的点z到点M(－，－1)的距离等于1，故点z的轨迹是以M为圆心，半径为1的圆，如图所示，||＝＝2.

所以|z|max＝2＋1＝3，|z|min＝2－1＝1.

1.已知z1＝5＋3i，z2＝5＋4i，下列选项中正确的是(　　)

A．z1>z2                     B．z1<z2

C．|z1|>|z2|                 D．|z1|<|z2|

答案：D　

解析：∵复数不能比较大小，∴A，B不正确；

又|z1|＝＝，

|z2|＝＝，

∴|z1|<|z2|，故C不正确，D正确.

2.复数z满足|z－2|－|z＋2|＝2，那么|z－2i|的最小值是(　　)

A．1       B． 

C．    D．2

答案：B　

解析：设z＝x＋yi(x，y∈R)，则由|z－2|－|z＋2|＝2，得－＝2，整理得x2－＝1(x≤－1)，所以|z－2i|＝＝＝≥，故选B．

3.当<m<1时，复数z＝(3m－2)＋(m－1)i在复平面上对应的点位于(　　)

A．第一象限        B．第二象限

C．第三象限        D．第四象限

答案：D　

解析：由<m<1得

∴复数z在复平面内对应的点位于第四象限.

4.在复平面内，表示复数z＝(m－3)＋2i的点位于直线y＝x上，则实数m的值为________．

答案：9　

解析：由表示复数z＝(m－3)＋2i的点位于直线y＝x上，得m－3＝2，解得m＝9.

5.如图，平行四边形OABC，顶点O，A，C分别表示0,3＋2i，－2＋4i，试求：

(1)表示的复数，表示的复数；

(2)所表示的复数；

(3)设P为复平面上一点且满足||＝||，求点P的轨迹方程．

解：(1)＝－，而对应的复数为3＋2i，

∴表示的复数为－3－2i；

∵＝，∴表示的复数为－3－2i.

(2)＝－，

∴所表示的复数为(3＋2i)－(－2＋4i)＝5－2i.

(3)设P(x，y)，

∵||＝|5－2i|＝＝，

||＝，由||＝||，

得x2＋y2＝29，即点P的轨迹方程为x2＋y2＝29.

[误区警示]　对复数的模理解不到位而致错

[典例]　试研究方程x2－5|x|＋6＝0在复数集上解的个数．

[错解]　将方程变为|x|2－5|x|＋6＝0⇒|x|＝2或|x|＝3⇒x＝±2或x＝±3，故共有4个.

[易错分析]　这里常出现将|x|看成“绝对值”，从而出现错误的解法，注意这里|x|是一个复数的模，它不等同于实数的绝对值，x2也不能写成|x|2.

[正解]　设x＝a＋bi(a，b∈R)，则原方程可化为

a2－b2－5＋6＋2abi＝0

⇒

⇒或或

即x＝±2或x＝±3或x＝±i.

故方程在复数集上的解共有6个.

[防范措施]　解题时要注意未知量的范围，在复数集

中x2与|x|2不是同一概念.

[类题试解]

已知复数z满足条件|z|2－|z|－6＝0，且复数z在复平面内的对应点为Z，求点Z的轨迹．

解：解法一：由|z|2－|z|－6＝0，

得(|z|－3)(|z|＋2)＝0.

∵|z|＋2≠0，∴|z|＝3，

∴复数z在复平面内对应的点Z的轨迹是以原点为圆心，3为半径的圆．

解法二：设z＝x＋yi(x，y∈R)，

则点Z的坐标为(x，y)．

由|z|2－|z|－6＝0，得x2＋y2－－6＝0，

即(－3)(＋2)＝0.

∵＋2≠0，

∴＝3，即x2＋y2＝9，

∴点Z的轨迹是以原点为圆心，3为半径的圆．