第6章 实数 章末复习 人教版七年级数学下册课件

这是一份第6章 实数 章末复习 人教版七年级数学下册课件，共20页。

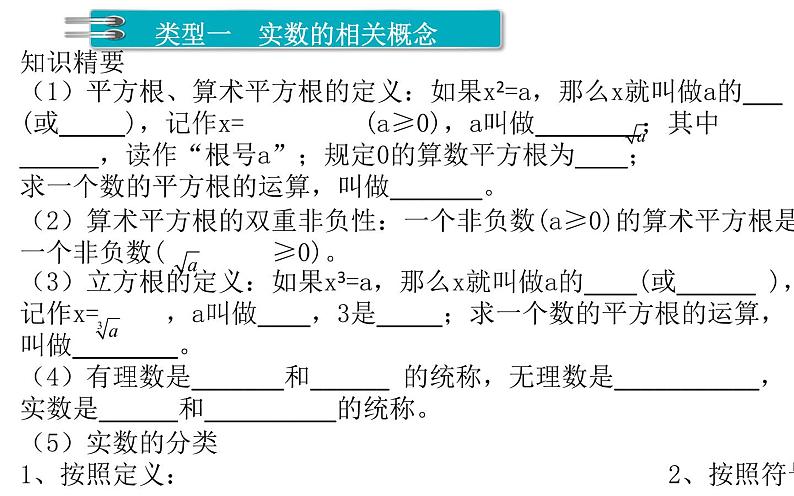
七年级数学下册（RJ） 教学课件 6 实数复习 第 六单元 实数类型一 实数的相关概念知识精要 （1）平方根、算术平方根的定义：如果x2=a，那么x就叫做a的___(或_____)，记作x= (a≥0)，a叫做________；其中 叫做a的______，读作“根号a”；规定0的算数平方根为____；求一个数的平方根的运算，叫做_______。（2）算术平方根的双重非负性：一个非负数(a≥0)的算术平方根是一个非负数( ≥0)。（3）立方根的定义：如果x3=a，那么x就叫做a的____(或______ )，记作x= ，a叫做____，3是_____；求一个数的平方根的运算，叫做________。（4）有理数是_______和______ 的统称，无理数是___________，实数是______和__________的统称。（5）实数的分类1、按照定义： 2、按照符号：类型一 实数的相关概念1、平方根与算数平方根例1 下列说法中，错误的是（　　）A．4的算术平方根是2 B． 的平方根是±9 C．8的平方根是 D．平方根等于1的实数是1练1 一个正数a的平方根分别是2m﹣1和﹣3m+ ，则这个正数a为_______．练2 . 是整数，则正整数n的最小值是_____ .类型一 实数的相关概念练3 实数a，b满足 ,则a+b= _______ .练4 求下列各式中x的值．（1）4（x+1）2﹣81＝0 （2） (2x－3)2＝(－7)2 类型一 实数的相关概念2、立方根例2 若 有意义，则a的取值范围是( )A.a=5 B. a ≥5 C. a<5 D. a为任意数变式 若 有意义，则a的取值范围是( ) A. a=5 B. a ≥5 C. a<5 D. a为任意数例3 下列说法①任何数的平方根都是两个②如果一个数有立方根，那么它一定有平方根③算术平方根一定是正数④非负数的立方根一定是非负数⑤若 ，则a＝b，正确的个数为______个.类型一 实数的相关概念练1. + ＝0，则x的值是_______ .练2 下列说法正确的有：_________．①对任意的数a有 ；②64的平方根是±8，立方根是±4；③ 表示a的平方根， 表示a的立方根；④一个数的立方根一定比这个数小；⑤ 一定是负数．类型一 实数的相关概念练3 观察下列各式，并用所得出的规律解决问题：（1） ≈1.414， ≈14.14， ≈141.4，…， ≈0.1732， ≈1.732， ≈17.32，…．由此可见，被开方数的小数点每向右移动____位，其算术平方根的小数点向____移动______位．（2）已知 ≈3.873， ≈1.225，则 ≈_____； ≈____．（3） ＝1， ＝10， ＝100，…，小数点的变化规律是_______________________________．（4）已知 ≈2.154， ≈﹣0.2154，则y＝______．类型一 实数的相关概念练4 求下列方程中x的值：(1) (2)64(2x+1)3=8 类型一 实数的相关概念3、实数相关概念例4 把下列各数分别填入相应的集合中0，﹣ ， ，3.1415926，﹣ ，2π，﹣1，0.13030030003…， ， （1）整数集合：{　 　…}（2）分数集合：{　 　…}（3）有理数集合：{　 　…}（4）无理数集合：{　 　…}类型一 实数的相关概念练1 有一个数值转换器，原理如下：当输入的x为64时，输出的y是（　　）A．2 B．2 C． D．±类型一 实数的相关概念练2 下列说法正确的有 .①两个无理数的和一定是无理数；②两个无理数的积一定是无理数；③一个有理数与一个无理数的和一定是无理数；④一个有理数与一个无理数的积一定是无理数．⑤不存在绝对值最小的无理数；⑥不存在绝对值最小的实数；⑦不存在与本身的算术平方根相等的数；⑧比正实数小的数都是负实数；⑨非负实数中最小的数是0．练3 若有理数a，b满足 a+b+3＝a﹣b+7 ，则a＝___，b＝___．类型一 实数的相关概念练4 已知实数a满足|2011﹣a|+ ＝，求a﹣20112的值为______．练5 已知 +5的小数部分为A，11﹣ 的小数部分为B，求：（1）A+B的值；（2）A﹣B的值．练6 计算： （精确到0.01）（注： ）.类型二 实数与数轴知识精要 实数与数轴上的点一一对应.例1 如图所示，数轴上表示3、 的对应点分别为C、B，点C是AB的中点，则点A表示的数是_______ .例2 如图，数轴上表示﹣ 的点可能是______ .类型二 实数与数轴练1 点A是数轴上的任意一点，则下列说法正确的是（　　）A．点A表示的数一定是整数 B．点A表示的数一定是分数 C．点A表示的数一定是有理数 D．点A表示的数可能是无理数练2 若点A在数轴上和原点相距2个单位，点B在数轴上和原点相距 个单位，则A，B两点之间的距离是　 　．练3 如图，半径为1个单位长度的圆，从数轴上的A点处沿数轴向右滚动一周后到达B点处，若点A表示的数为﹣1，则点B对应的数是　 　．类型三 实数的大小比较知识精要 与有理数规定的大小一样，数轴上右边的点表示的实数比左边的点表示的实数大.在实数范围内：1.正数大于零，负数小于零，正数大于负数；2.两个正数，绝对值大的数较大；3.两个负数，绝对值大的数反而小.例1 估计﹣3的值在（　　）A．1和2之间 B．﹣1和0之间 C．2和3之间 D．﹣2和﹣1之间总结：估计一个有理数的算术平方根的近似值，必须先判断这个有理数位于哪两个数的平方之间。类型三 实数的大小比较练1 通过估算比较下列各组数的大小：（1） ____ （2） _____ 2.1练2 比较下列各组数的大小；（1） ____ （2） ____ （3）5____ （4）﹣ ____﹣（5） ____1.5 （6） ____类型四 实数的运算练1 计算：（1）﹣12020+ ﹣ +|2﹣ | （2） | ﹣ |+ ﹣ +（ ）2 （3）（﹣1）2+ +| ﹣3|+ （4）|1﹣ |+ ﹣ （ ﹣ ）类型四 实数的运算练2 已知实数a，b互为相反数，c，d互为倒数，e是 的整数部分，f是 的小数部分，求代数式 的值．练3 已知 ＝3，3a﹣b+1的平方根是±4，c是 的整数部分，求a+b+2c的平方根．类型五 实数的应用例 小明想用一块长宽之比为4：3且面积为444cm2的长方形纸片，沿着边的方向剪成面积为441cm2正方形纸片．你认为小明的想法能实现吗？请说明理由．类型二 实数与数轴练 习. 某小区为了促进全民健身活动的开展，决定在一块面积约为1000m2的正方形空地上建一个篮球场，已知篮球场的面积为420m2，其中长是宽的 倍，篮球场的四周必须留出1m宽的空地，请你通过计算说明能否按规定在这块空地上建一个篮球场？