广东省广州市外国语学校2022-2023学年七年级数学上学期期末考试试卷

2022－2023学年度广州外国语学校初一第一学期

期末数学考卷

考试范围：初一上册；考试时间：120分钟；

注意事项：

1.答题前填写好自己的姓名、班级、考号等信息

2.请将答案正确填写在答题卡上

第I卷（选择题）

一、单选题（共10题，每题3分，共30分）

1. 下列为负数的是（  ）

A.  B.  C. 0 D.

【答案】D

【解析】

【分析】根据正负数的意义分析即可；

【详解】解：A、=2是正数，故该选项不符合题意；

B、是正数，故该选项不符合题意；

C、0不是负数，故该选项不符合题意；

D、是负数，故该选项符合题意．

故选：D．

【点睛】本题考查正负数的概念和意义，熟练掌握绝对值、算术平方根和正负数的意义是解决本题的关键．

2. 单项式的次数是（     ）

A. －1 B. 1 C. 2 D. 3

【答案】D

【解析】

【分析】根据单项式的次数即为单项式中所有字母的指数和，据此解答即可．

【详解】解：单项式的次数是，

故选：D．

【点睛】本题考查了单项式次数的定义，熟记相关定义是解本题的关键．

3. 下列各式中，运算正确的是（    ）

A.  B.  C.  D.

【答案】B

【解析】

【分析】直接根据合并同类项的法则计算即可．

【详解】解：A、与不是同类项，不能合并，不合题意；

B、，正确，符合题意；

C、与不同类项，不能合并，不合题意；

D、，不合题意；

故选：B．

【点睛】此题考查的是合并同类项，掌握其运算法则是解决此题的关键．

4. 若x的相反数是2，|y|＝5，且x+y＜0，则x﹣y的值是（　　）

A. 3 B. 3或﹣7 C. ﹣3或﹣7 D. ﹣7

【答案】A

【解析】

【分析】根据题意，结合 x+y<0 ，求出x、y的值，然后求出答案．

【详解】解：∵﹣2的相反数是2，

∴x＝﹣2．

∵|y|＝5，

∴y＝±5．

∵x+y＜0，

∴x＝﹣2，y＝﹣5．

∴x﹣y＝﹣2﹣（﹣5）＝﹣2+5＝3．

故选：A．

【点睛】本题考查了求代数式的值，绝对值的意义，以及相反数的定义，解题的关键是确定x、y的值．

5. 某商场周年庆期间，对销售的某种商品按成本价提高30%后标价，又以9折优惠卖出，结果每件商品仍可获利85元，设这种商品每件的成本是元，根据题意，可得到的方程是（    ）

A.  B.

C.  D.

【答案】A

【解析】

【分析】由题意可知：成本+利润=售价，设这种商品每件的成本是元，则提高30%后的标价为元；打9折出售，则售价为，列出方程即可.

【详解】解：由题意可知：售价=成本+利润，

设这种商品每件的成本是元，则提高30%后的标价为元；

打9折出售，则售价为；

根据：售价=成本+利润，列出方程：

故选：A.

【点睛】本题考查了一元一次方程的应用，熟练掌握等量关系：“成本+利润=售价”是解答本题的关键.

6. 点A、B、C在同一直线上，，，则（    ）．

A. 12cm B. 8cm C. 12cm或8cm D. 以上均不对

【答案】C

【解析】

【分析】分两种情况分别计算，即可分别求得．

【详解】解：当点C在线段AB上时，BC=AB-AC=10-2=8(cm)，

当点C在线段BA的延长线上时，BC=AB+AC=10+2=12(cm)，

故BC的长为12cm或8cm，

故选：C．

【点睛】本题考查了求线段的和差，采用分类讨论的思想是解决本题的关键．

7. 已知∠1=43°27′，则∠1的余角分别为（   ）

A. 46°33′ B. 46°73′ C. 136°73′ D. 136°33′

【答案】A

【解析】

【分析】根据余角的定义进行计算即可．

【详解】解：∵∠1=43°27′，
∴∠1的余角=90°-43°27′=46°33′．

故选：A．

【点睛】此题考查了余角的定义，解决本题的关键是如果两个角的和是90°，那么这两个角互余．

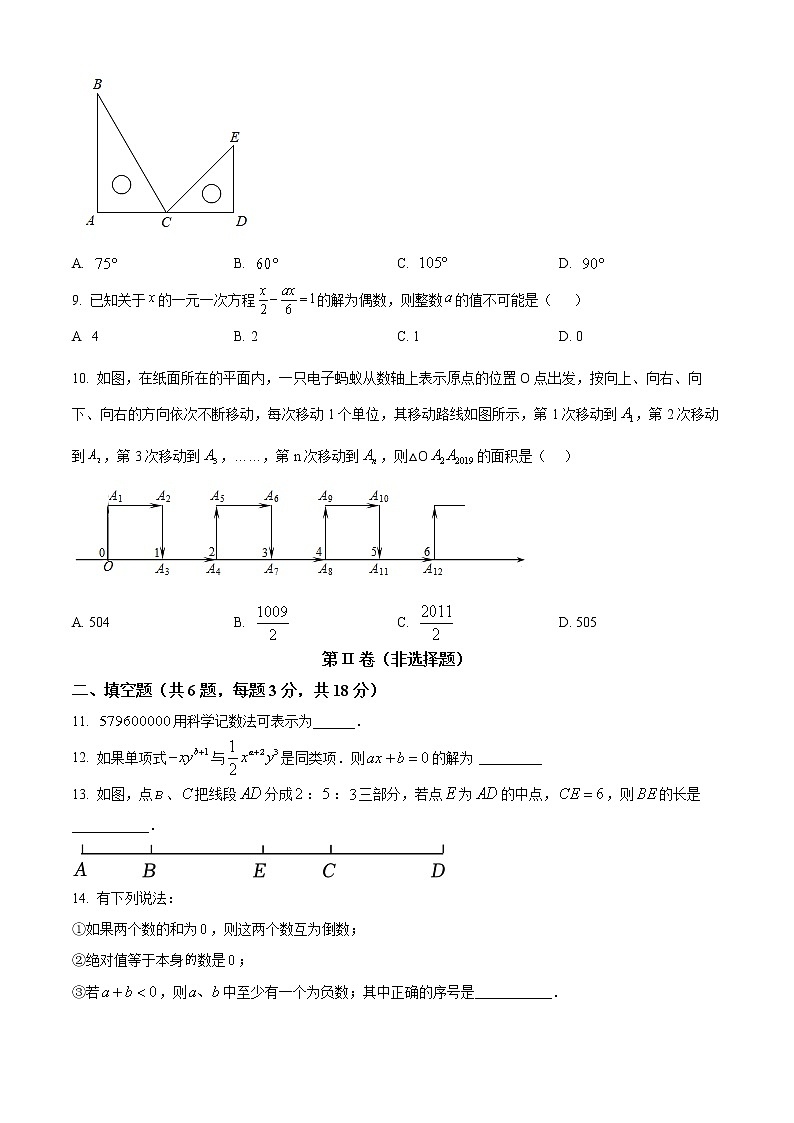
8. 如图，将一副三角板()按图中的方式摆放，A、C、D三点在同一条直线上，则（      ）

A.  B.  C.  D.

【答案】A

【解析】

【分析】利用平角的定义即可求解．

【详解】解：∵，

∴，

∴，

故选：A．

【点睛】本题考查平角的定义，三角板的特殊内角，掌握三角板的内角度数是解决问题的关键．

9. 已知关于的一元一次方程的解为偶数，则整数的值不可能是（   ）

A. 4 B. 2 C. 1 D. 0

【答案】C

【解析】

【分析】由得，，解得，，的值是偶数，满足条件的值分别是，，，，由此即可求解．

详解】解：由得，，解得，，

∵的值是偶数，

的值可能为、、、时，的值分别是，，，，符合题意，

∴的值可能为，，、，

∴整数的值不可能是．

故选：．

【点睛】本题主要考查一元一次方程中未知数的取值情况，掌握一元一次方程中未知数的取值不同求参数是解题的关键．

10. 如图，在纸面所在的平面内，一只电子蚂蚁从数轴上表示原点的位置O点出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其移动路线如图所示，第1次移动到，第2次移动到，第3次移动到，……，第n次移动到，则△O的面积是（   ）

A. 504 B.  C.  D. 505

【答案】B

【解析】

【分析】根据图可得移动4次完成一个循环，观察图形得出OA4n=2n，处在数轴上的点为A4n和A4n-1.由OA2016=1008，推出OA2019=1009，由此即可解决问题．

【详解】解： 观察图形可知： OA4n=2n，且点A4n和点A4n-1在数轴上，
又2016=504×4，∴A2016在数轴上，且OA2016=1008，
∵2019=505×4-1，∴点A2019在数轴上，OA2019=1009，
∴△OA2A2019的面积=×1009×1=，
故选：B．

【点睛】本题考查三角形面积，数轴等知识，解题的关键是学会探究规律，利用规律解决问题，属于中考常考题型．

第II卷（非选择题）

二、填空题（共6题，每题3分，共18分）

11. 用科学记数法可表示为______．

【答案】

【解析】

【分析】科学记数法的表现形式为的形式，其中，n为整数，确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，n是正数，当原数绝对值小于1时n是负数；由此进行求解即可得到答案．

【详解】解：

故答案为：．

【点睛】本题主要考查了科学记数法，解题的关键在于能够熟练掌握科学记数法的定义．

12. 如果单项式与是同类项．则的解为 _________

【答案】

【解析】

【分析】根据同类项的定义，分别得到关于和关于的一元一次方程，解得和的后代入方程，再解关于的一元一次方程，即可得到答案．

【详解】解：∵单项式与是同类项，

∴，，

解得：，，

把，代入方程，

得：，

解得：．

故答案为：．

【点睛】本题考查解一元一次方程和同类项．正确掌握同类项定义和解一元一次方程的方法是解题的关键．

13. 如图，点、把线段分成：：三部分，若点为的中点，，则的长是 ___________．

【答案】

【解析】

【分析】设，，，根据已知分别用x表示出，从而得出的长．

【详解】解：设，，，

∴，

∵为的中点，

∴，

又∵，

∴，

∴，

∴，

∴，

故的长为．

故答案为：．

【点睛】本题考查了线段的计算，理解中点和比的意义，用含x的式子表示出各线段的长并求出x是解题的关键．

14. 有下列说法：

①如果两个数的和为，则这两个数互为倒数；

②绝对值等于本身的数是；

③若，则中至少有一个为负数；其中正确的序号是___________．

【答案】③

【解析】

【分析】根据相反数定义、绝对值意义、有理数加法运算法则对每一项进行判断，最后得出结论．

【详解】解：如果两个数的和为，则这两个数互为相反数．因此①错误；

绝对值等于本身的数是，因此②错误；

根据有理数的加法法则可知：若，则中至少有一个为负数这个说法正确，故③正确

故答案为：③

【点睛】本题考查了绝对值的意义、相反数的定义、有理数加法法则，熟练掌握对应性质是解题的关键．

15. 如图，货轮O在航行过程中，发现灯塔A在它南偏东60°的方向上；同时，它又发现了客轮B；仿照表示灯塔方位的方法，客轮B在货轮的_______方向．

【答案】北偏东40°##东偏北50°

【解析】

【分析】根据方位角的表示方法即可得到答案．

【详解】解：仿照表示灯塔方位的方法，客轮B在货轮的北偏东40°的方向上，

故答案为：北偏东40°

【点睛】此题考查了方位角，熟练掌握方位角的表示方法是解题的关键．

16. 有一个十进制的六位数（其中a、b、c、d、e分别是这个六位数的万位、千位、百位、十位、个位上的数字）乘以3后，变成一个新的六位数，则原来的六位数是__________．

【答案】

【解析】

【分析】设5位数为y，根据六位数乘以3变成新六位数列出方程求解即可．

【详解】解：设5位数为y，由题意，得

，

解得．

则这个六位数为：．

故答案为：．

【点睛】本题主要考查了一元一次方程的应用，正确理解题意找到等量关系列出方程是解题的关键．

三、解答题

17. 计算：（1）；

（2）

【答案】（1）1；（2）-55．

【解析】

【分析】（1）原式利用乘法分配律计算即可求出值；
（2）原式先计算乘方及绝对值运算，再计算乘除运算，最后算加减运算即可求出值．

【详解】（1）原式=2-9+14-6=1；
（2）原式=-1-18×3=-1-54=-55．

【点睛】此题考查有理数的混合运算，熟练掌握运算法则是解题的关键．

18. 解方程：

（1）                （2）

【答案】（1）x＝（2）x＝4．

【解析】

【分析】（1）方程移项合并，把x系数化为1，即可求出解；

（2）方程去分母，去括号，移项合并，把x系数化为1，即可求出解．

【详解】（1）移项合并得：8x＝4，

解得：x＝；    

（2）

去分母得：2x＋2−4＝8+2-x，

移项合并得：3x＝12，

解得：x＝4．

【点睛】此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，把未知数系数化为1，求出解．

19. 如图，已知线段a，b．

（1）请用没有刻度的直尺和圆规按下列要求作图，保留作图痕迹；

①作线段AB＝a；

②延长线段AB到C，使BC＝b．

（2）在（1）的条件下，若AB＝8，BC＝5，点D是线段AB的中点，点E是线段AC的中点，求线段DE的长．

【答案】（1）见解析    （2）

【解析】

【分析】（1）①先作射线AM，然后以点A为圆心，线段a的长度为半径画弧，交射线于一点，即可得出线段AB；

②以B为圆心，线段b的长度为半径画弧，交射线AM于点C，即可画出线段BC；

（2）先求出线段AC=13，根据E是AC的中点，得出AEAC，D是AB的中点，得出ADAB＝4，最后算出结果即可．

【小问1详解】

解：线段AB即为所求线段AB＝a；线段BC即为所求线段BC＝b，如图所示：

【小问2详解】

解：∵AB＝8，BC＝5，

∴AC＝AB+BC＝8+5＝13，

∵E是AC的中点，

∴AEAC，

∵D是AB的中点，

∴ADAB＝4，

∴DE＝AE﹣AD=．

【点睛】本题主要考查了作一条线段等于已知线段，线段中点的有关计算，分别求出AE，AD＝4，是解题的关键．

20. 已知有理数a，b，c的位置如图所示．

（1）用“>”或“<”填空∶         0，     0．

（2）化简式子：．

【答案】（1），   

（2）

【解析】

【分析】（1）根据a，b，c在数轴上的位置以及加法法则和减法法则解答即可；

（2）根据绝对值的意义去掉绝对值符号，再去括号合并同类项．

【小问1详解】

解：，

．

．

故答案为：，；

【小问2详解】

解：

【点睛】本题考查了利用数轴比较式子的大小，化简绝对值，以及整式的加减，熟练掌握绝对值的意义和整式加减的运算法则是解答本题的关键．

21. 如图，是一个正方体纸盒的表面展开图，纸盒中相对两个面上的数互为倒数．

（1）填空：        ，        ；

（2）先化简，再求值：．

【答案】（1），；   

（2）．

【解析】

【分析】（1）先根据正方体的平面展开图确定a、b、c所对的面的数字，再根据相对的两个面上的数互为倒数，确定a、b、c的值；

（2）先去括号，再合并同类项化简代数式后代入求值即可．

【小问1详解】

解：由长方体纸盒的平面展开图知，a与、b与、c与2是相对的两个面上的数字或字母，

因为相对的两个面上的数互为倒数，

所以，，，

故答案为：，

【小问2详解】

解：

．

将，，代入上式可得：

原式．

【点睛】本题考查了正方体的平面展开图、倒数及整式的加减化简求值，解决本题的关键是根据平面展开图确定a、b、c的值．

22. 如图，O为直线AB上一点，，平分，．

（1）求出的度数；

（2）试判断是否平分，并简要说明理由．

【答案】（1）   

（2）平分,理由见解析

【解析】

【分析】（1）根据角平分线的定义以及平角的性质进行解答即可；

（2）分别求出和的度数，即可得出结论．

【小问1详解】

解：∵，平分，

∴，

∴，

答：的度数为；

【小问2详解】

∵，，

∴，

∴，

∴，

∴，

∴平分．

【点睛】本题考查了角平分线的定义，角度计算，读懂题意，熟练掌握相关定义是解本题的关键．

23. 为有效落实双减工作，切实做到减负提质，很多学校高度重视学生的体育锻炼，并不定期举行体育比赛．已知在一次足球比赛中，胜一场得3分，平一场得1分，负一场得0分，某队在已赛的11场比赛中保持连续不败，共得25分，求该队获胜的场数．

【答案】7场

【解析】

【分析】设该队获胜x场，则平场，利用总得分 获胜场次数 打平场次数，即可得出一元一次方程，解方程即可求得答案．

【详解】设该队获胜x场，则平场，

依题意得：，解得：．

答：该队获胜7场．

【点睛】本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．

24. 【背景知识】数轴上A、B两点在对应的数为a，b，则A、B两点之间的距离定义为：．

【问题情境】已知点A、B、O在数轴上表示数分别为-4、10和0，点M、N分别从O、B出发，同时向左匀速运动，点M的速度是每秒1个单位长度，点N的速度是每秒3个单位长度，设运动的时间为t秒（）．

（1）填空：

①                   ；

②用含t的式子表示：         ；          ；

（2）当t为何值时，恰好有；

（3）求的最小值．

【答案】（1）①4，10；②，；（2）或；（3）14

【解析】

【分析】（1）①由题意可直接进行求解；

②由题意可得点M在数轴表示的数为-t，点N在数轴表示的数为10-3t，然后根据数轴上的两点距离可求解；

（2）由（1）可分点M在点A的右边、点M在点A的左边和点M、N都在点A的左边，然后列方程求解即可；

（3）由可看作是到和4的距离，进而可分当时，当时和当时，然后进行求解比较即可．

【详解】解：（1）①由点A、B、O在数轴上表示的数分别为-4、10和0，可得：

，

故答案为4，10；

②由点M、N分别从O、B出发，同时向左匀速运动，点M的速度是每秒1个单位长度，点N的速度是每秒3个单位长度，设运动的时间为t秒，可得点M、N的运动路程分别为：t，3t；

∴点M在数轴表示的数为-t，点N在数轴表示的数为10-3t，

∴，

故答案为，；

（2）由（1）可得：当点N追上点M时，则有，解得：，

∴①当点M在点A的右边时，即，则有，解得：（不符合题意，舍去）；

②当点M在点A的左边时，即，则有，＞4，符合题意；

③当点N追上点M后，即，点M、N都在点A的左边，则有，解得：＞5，符合题意；

综上所述：当时，或；

（3）由可看作是到和4的距离，则有：

当时，无最小值；

当时，，

当时，，无最小值，

综上所述：当当时，有最小值，最小值为14．

【点睛】本题主要考查数轴上的两点距离、一元一次方程的解法及线段的和差关系，熟练掌握数轴上的两点距离、一元一次方程的解法及线段的和差关系是解题的关键．

25. 如图1，将一副三角板的直角顶点叠放在一起．

【观察分析】

（1）若，则____________；若，则__________．

【猜想探究】

（2）请你猜想与有何关系，并说明理由；

【拓展应用】

（3）如图2，若将两个同样的三角尺锐角的顶点重合在一起，请你猜想与有何关系，并说明理由．

【答案】（1），；（2），理由见解析；（3），理由见解析

【解析】

【分析】试题分析：（1）本题已知两块直角三角尺实际就是已知三角板的各个角的度数，根据角的和差就可以求出∠ACB，∠DCE的度数；
（2）根据前个小问题的结论猜想∠ACB与∠DCE的大小关系，结合前问的解决思路得出证明．
（3）根据（1）（2）解决思路确定∠DAB与∠CAE的大小并证明．

【详解】解：（1）∵，，
∴，

∵，

∴；

∵，，

∴，

∵，

∴，

故答案为：，；

（2），理由：

∵，，

∴，

∵，

∴；

（3），理由：

∵，，

∴，

∵，

∴．

【点睛】考查角的计算，角的和差，余角和补角，直角三角形的性质，数形结合是解题的关键．