




- 5.4二次函数的图象和性质第4课时 课件+教案 课件 1 次下载
- 5.5确定二次函数的表达式 课件+教案 课件 1 次下载
- 5.7二次函数的应用 第1课时 课件+教案 课件 2 次下载
- 5.7二次函数的应用 第2课时 课件+教案 课件 1 次下载
- 6.1随机事件 课件+教案 课件 1 次下载
初中数学青岛版九年级下册5.3二次函数精品课件ppt
展开5.6 二次函数的图象与一元二次方程
教学目标
【知识与能力】
1、能够利用二次函数的图像求一元二次方程的近似根。
2、进一步发展学生的估算能力。
【过程与方法】
1、经历用图像法求一元二次方程的近似根的过程,获得用图像法求方程近似根的体验
2、利用图像法求一元二次方程的近似根,重要的是学生懂得这种求解方程的思路,体验数形结合思想。
【情感态度价值观】
通过利用二次函数的图像估计一元二次方程的根,进一步掌握二次函数的图像与轴的交点坐标和一元二次方程的根的关系,提高估算能力。
教学重难点
【教学重点】
1、经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系。
2、用图像法求一元二次方程的近似根
【教学难点】
利用二次函数的图像求一元二次方程的近似根
课前准备
无
教学过程
一创设问题情境,引入新课
上节课我们学习了二次函数y=ax2+bx+c 的图像与x 轴交点有三种情况:有两个交点、一个交点、没有交点。二次函数y=ax2+bx+c 的图像与x 轴的交点坐标一元二次方程ax2+bx+c=0的根的关系。懂得了二次函数y=ax2+bx+c 的图像与x 轴交点的横坐标就是当y =0时的一元二次方程的根。于是我们在不解方程的情况下,只要知道二次函数的图像与x 轴交点的横坐标即可.但是, 在图像上我们很难准确地求出方程的解,所以要进行估算.本节课我们将学习利用二次函数的图像估计一元二次方程的根.
1.讲授新课
利用二次函数的图像估计一元二次方程的根.
右图是函数的图像
从图像上来看, 二次函数y=x2+2x-10 的图像与x 轴交点的横坐标一个在-5与-4之间,另一个在2于3之间,所以方程x2+2x-10=0的一个根在-5与-4之间,另一个在2与3之间.这只是大概范围,究竟更近于哪一个数呢?请同学们讨论解决.
① 先求-5与-4之间的根,利用计算器进行探索
x | -4.1 | -4.2 | -4.3 | -4.4 |
y | -1.39 | -0.76 | -0.11 | 0.56 |
∴x= - 4.3是方程的一个近似根
②再求2与3之间的根,利用计算器进行探索
x | 2.1 | 2.2 | 2.3 | 2.4 |
y | -1.39 | -0.76 | -0.11 | 0.56 |
∴x=2.3是方程的另一个近似根确定方程x2+2x-10=0的解,用求根公式求是多少
由此可知,方程x2+2x-10=0的近似根为:x1≈-4.3,x2≈2.3.
总结一下:
如何利用二次函数的图象估计一元二次方程的两根的值?基本步骤是什么?
(1)画出二次函数y=ax2+bx+c的图象;
(2)根据图象确定抛物线y=ax2+bx+c与x轴的两个交点分别在哪两个相邻的整数之间
(3)利用计算器探索其解的十分位数字。
从而确定方程的近似根
做一做
例1利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
(1).用描点法作二次函数y=x2+2x-10的图象;
(2) 作直线y=3;
(3).观察估计抛物线y=x2+2x-10和直线y=3的交点的横坐标
(4).确定方程x2+2x-10=3的解;
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).
由此可知,方程x2+2x-10=3的近似根为:
x1≈-4.7,x2≈2.7
也可以这样解
解法二:
(1).原方程可变形为x2+2x-13=0;
(2).用描点法作二次函数y=x2+2x-13的图象(3).观察估计抛物线y=x2+2x-13和x轴的交点的横坐标;由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值) (3).确定方程x2+2x-10=3的解;
由此可知,方程x2+2x-10=3的近似根为:
x1≈-4.7,x2≈2.7
随堂练习:用二次函数的图象求一元二次方程-2x2+4x+1=0的近似根.
(1).用描点法作二次函数y=-2x2+4x+1的图象;
(2).观察估计二次函数y=-2x2+4x+1的图象与
x轴的交点的横坐标;
图象可知,图象与x轴有两个交点,其横坐标一
个在-1与0之间,另一个在2与3之间,分别约
为-0.2和2.2(可将单位长再十等分,借助计算
器确定其近似值
由此可知,方程-2x2+4x+1=0的近似根为:
x1≈-0.2,x2≈2.2.
布置作业 70页1 72页 1,2
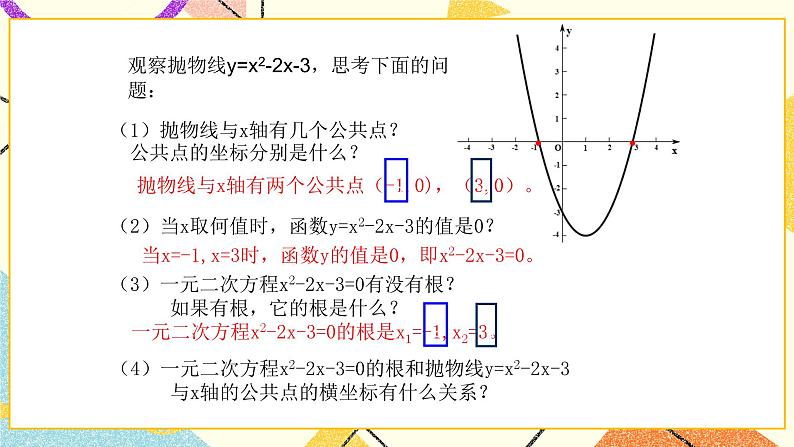
数学青岛版5.3二次函数精品ppt课件: 这是一份数学青岛版<a href="/sx/tb_c75845_t3/?tag_id=26" target="_blank">5.3二次函数精品ppt课件</a>,共15页。PPT课件主要包含了学习目标,观察与思考,yx2-2x-3,转化为等内容,欢迎下载使用。
浙教版九年级上册1.2 二次函数的图象精品ppt课件: 这是一份浙教版九年级上册1.2 二次函数的图象精品ppt课件,文件包含浙教版数学九上121二次函数的图象课件ppt、浙教版数学九上121二次函数的图象教案doc、浙教版数学九上121二次函数的图象学案doc等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
初中数学第5章 几何证明初步5.6 几何证明举例精品习题课件ppt: 这是一份初中数学第5章 几何证明初步5.6 几何证明举例精品习题课件ppt,文件包含《几何证明举例》课件ppt、练习1_几何证明举例ppt、练习2_几何证明举例ppt、练习3_几何证明举例ppt、练习4_几何证明举例ppt、练习5_几何证明举例ppt、《几何证明举例》习题doc、例题_几何证明举例ppt、导入_几何证明举例ppt、等腰三角形拓展练习_几何证明举例ppt、《几何证明举例》教案doc等11份课件配套教学资源,其中PPT共29页, 欢迎下载使用。













