2023年中考数学一轮复习《数据的集中与波动趋势》课时练习（含答案）

2023年中考数学一轮复习

《数据的集中与波动趋势》课时练习

一              、选择题

1.5月份某一周的日最高气温(单位：℃)分别为25，28，30，29，31，32，28，这周的日最高气温的平均值为(　　)

A.28℃        B.29℃        C.30℃        D.31℃

2.在一次“爱心互助”捐款活动中，某班第一小组8名同学捐款的金额(单位：元)如下表所示：

这8名同学捐款的平均金额为(　　)

A.3.5元                 B.6元         C.6.5元         D.7元

3.有m个数的平均数是x，n个数的平均数是y，则这(m+n)个数的平均数为(  )

A.

4.某校开展了以“爱我家乡” 为主题的艺术活动，从九年级5个班收集到的艺术作品数量(单位：件)分别为 48，50，47，44，50，则这组数据的中位数是(  )

A.44        B.47       C.48         D.50

5.在一次体检中，甲、乙、丙、丁四位同学的平均身高为1.65米，而甲、乙、丙三位同学的平均身高为1.63米，下列说法一定正确的是(　　)

A．四位同学身高的中位数一定是其中一位同学的身高 

B．丁同学的身高一定高于其他三位同学的身高

C．丁同学的身高为1.71米 

D．四位同学身高的众数一定是1.65

6.世界因爱而美好，在今年我校的“献爱心”捐款活动中，九年级三班50名学生积极加献爱心捐款活动，班长将捐款情况进行了统计，并绘制成了统计图，根据图中提供的信息，捐款金额的众数和中位数分别是（  ）

A.20、20     B.30、20     C.30、30     D.20、30

7.李华根据演讲比赛中九位评委所给的分数制作了表格：

对9个评委所给的分数,去掉一个最高分和一个最低分后,表中数据一定不发生变化的是（    ）

  A.平均数                        B.中位数                        C.方差                     D.众敎

8.面试时，某应聘者的学历、经验和工作态度的得分分别是70分、80分、60分，若依次按照1：2：2的比例确定成绩，则该应聘者的最终成绩是(　　)

A.60分        B.70分        C.80分        D.90分

二              、填空题

9.若数据2，3，－1，7，x的平均数为2，则x=      .

10.丁丁中考模拟考试中，语文、数学、英语、理化、政史的得分依次是125、148、145、150、135，则这组数据的中位数是______.

11.为参加“初中毕业生升学体育考试”，小静同学每天进行仰卧起坐的练习，并记录下其中5天的成绩(单位：个)分别为：45，40，46，45，48.这组数据的众数是     、中位数是     

12.某次数学测验满分为100(单位：分)，某班的平均成绩为75，方差为10.若把每位同学的成绩按满分120进行换算，则换算后的平均成绩与方差分别是__________.

13.为了解某班学生体育锻炼的用时情况，收集了该班学生一天用于体育锻炼的时间(单位：小时)，整理成如图的统计图．则该班学生这天用于体育锻炼的平均时间为　　小时．

14.已知一组从小到大排列的数据：1，x，y，2x，6，10的平均数与中位数都是5，则这组数据的众数是　　.

三              、解答题

15.车间有20名工人，某一天他们生产的零件个数统计如下表．

车间20名工人某一天生产的零件个数统计表

(1)求这一天20名工人生产零件的平均个数．

(2)为了提高大多数工人的积极性，管理者准备实行“每天定额生产，超产有奖”的措施．如果你是管理者，

从平均数、中位数、众数的角度进行分析，你将如何确定这个“定额”？

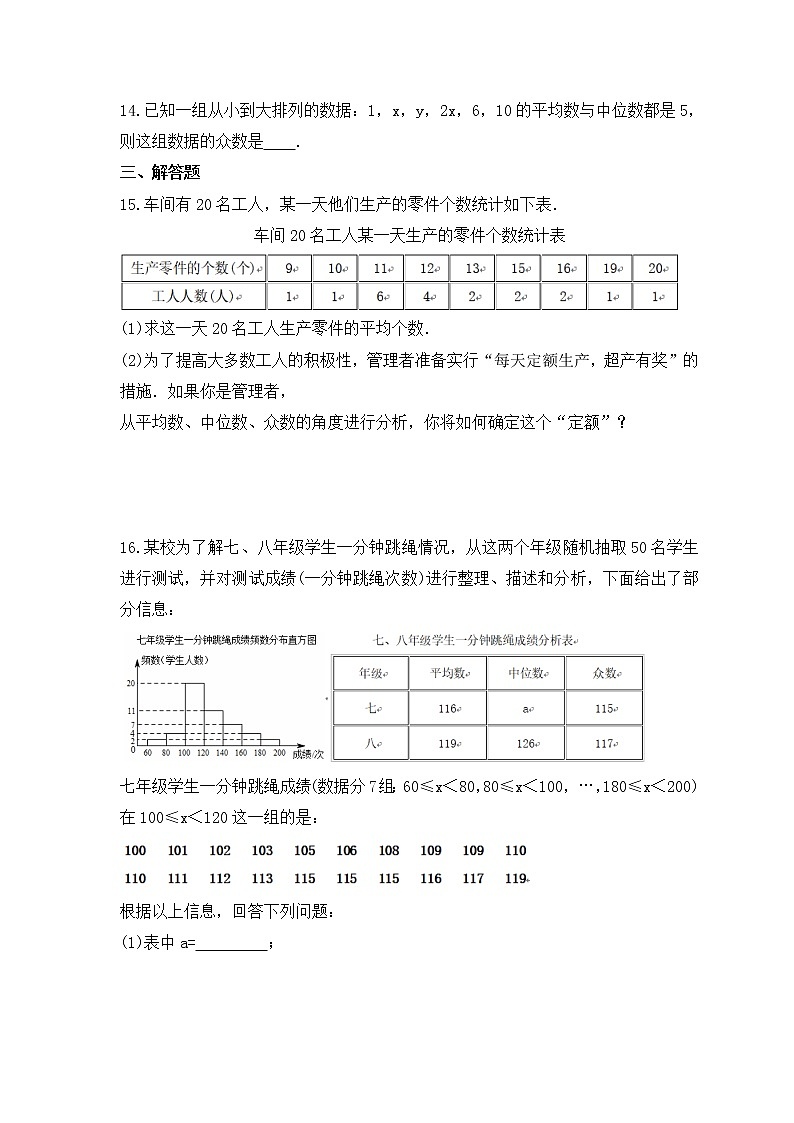
16.某校为了解七、八年级学生一分钟跳绳情况，从这两个年级随机抽取50名学生进行测试，并对测试成绩(一分钟跳绳次数)进行整理、描述和分析，下面给出了部分信息：

七年级学生一分钟跳绳成绩(数据分7组：60≤x＜80，80≤x＜100，…，180≤x＜200)在100≤x＜120这一组的是：

根据以上信息，回答下列问题：

(1)表中a=　   　；

(2)在这次测试中，七年级甲同学的成绩122次，八年级乙同学的成绩125次，他们的测试成绩，在各自年级所抽取的50名同学中，排名更靠前的是　   　(填“甲”或“乙”)，理由是　   　．

(3)该校七年级共有500名学生，估计一分钟跳绳不低于116次的有多少人？

17.为增强学生的身体素质，教育行政部门规定每位学生每天参加户外活动的平均时间不少于1小时．为了解学生参加户外活动的情况，对部分学生参加户外活动的时间进行抽样调查，并将调查结果绘制作成如下两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

（1）在这次调查中共调查了多少名学生？

（2）求户外活动时间为1.5小时的人数，并补充频数分布直方图；

（3）户外活动时间的众数和中位数分别是多少？

（4）若该市共有20000名学生，大约有多少学生户外活动的平均时间符合要求？

18.某校学生会向全校1900名学生发起了“心系雅安”捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列是问题：

（1）本次接受随机抽样调查的学生人数为   ，图①中m的值是   ；

（2）求本次调查获取的样本数据的平均数、众数和中位数；

（3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．

参考答案

1.B

2.C

3.C

4.C

5.C.

6.C

7.C

8.B.

9.答案为：-1.

10.答案为：145.

11.答案为：45、45.

12.答案为：90，14.4.

13.答案为：1.15．

14.答案为：6.

15.解：(1)=×(9×1+10×1+11×6+12×4+13×2+15×2+16×2+19×1+20×1)=13(个)；

答：这一天20名工人生产零件的平均个数为13个；

(2)中位数为=12(个)，众数为11个，

当定额为13个时，有8人达标，6人获奖，不利于提高工人的积极性；

当定额为12个时，有12人达标，6人获奖，不利于提高大多数工人的积极性；

当定额为11个时，有18人达标，12人获奖，有利于提高大多数工人的积极性；

∴定额为11个时，有利于提高大多数工人的积极性．

16.解：(1)∵七年级50名学生成绩的中位数是第25、26个数据的平均数，

而第25、26个数据分别是117、119，

∴中位数a==118，故答案为：118；

(2)∴在各自年级所抽取的50名同学中，排名更靠前的是甲，

理由是甲的成绩122超过中位数118，乙的成绩125低于其中位数126，

故答案为：甲，甲的成绩122超过中位数118，乙的成绩125低于其中位数126．

(3)估计一分钟跳绳不低于116次的有500×=270(人)．

17.解：（1）调查的总人数是10÷20%=50（人）；

（2）户外活动时间是1.5小时的人数是50×24%=12（人），

；

（3）中数是1小时，中位数是1小时；

（4）学生户外活动的平均时间符合要求的人数是20000×（1﹣20%）=16000（人）．

答：大约有16000学生户外活动的平均时间符合要求．

18.解：（1）根据条形图4+16+12+10+8=50（人），m=100﹣20﹣24﹣16﹣8=32；

（2）∵=（5×4+10×16+15×12+20×10+30×8）/50=16，

∴这组数据的平均数为：16，

∵在这组样本数据中，10出现次数最多为16次，∴这组数据的众数为：10，

∵将这组样本数据按从小到大的顺序排列，其中处于中间的两个数都是15，

∴这组数据的中位数为：0.5（15+15）=15；

（3）∵在50名学生中，捐款金额为10元的学生人数比例为32%，

∴由样本数据，估计该校1900名学生中捐款金额为10元的学生人数比例为32%，

有1900×32%=608，

∴该校本次活动捐款金额为10元的学生约有608名．

故答案为：50，32．