浙教版九年级下册第二章 直线与圆的位置关系2.1 直线和圆的位置关系优秀课件ppt

导入新课

一、创设情景，引出课题

创设情景：

下雨天，你快速转动雨伞时，雨水飞出的情景你看见过吗？工人师傅用砂轮打磨工件飞出火星的情景见过吗？

(动画演示)

照下述步骤作图：

如图，在⊙O上任取一点A．连结OA．过点A作直线l⊥OA．

思考以下问题（可与你的同伴交流）：

（1）圆心O到直线l的距离和圆的半径有什么关系？

（2）直线l与⊙O的位置有什么关系？根据什么？

（3）由此你发现什么？

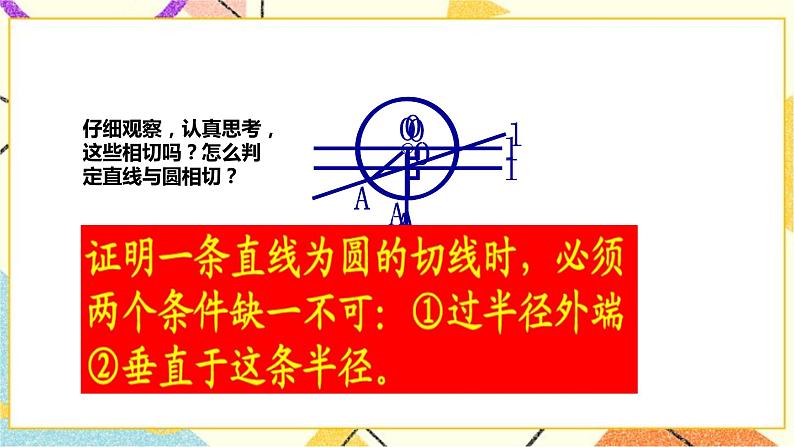
解：（1）圆心O到直线l的距离等于圆的半径长．

（2）直线l与⊙O相切，根据d＝r直线与⊙O相切．

（3）经过半径的外端并且垂直这条半径的直线是圆的切线．

特征①：直线l经过半径OA的外端点A．

特征②：直线l垂直于半径OA．

几何语言：

∵l⊥OA，且OA为圆O的半径，

∴l是⊙O的切线．

本节开头是让学生通过作图来发现直线与圆相切的判定定理，教学中可按下列步骤进行．

（1）让学生按课本要求作出直线l，并提问，点O到直线l的距离，与圆O的半径有怎样的关系？

（2）直线l与圆O的位置关系有什么关系？根据什么？可启发学生回顾上节课关于直线与圆的位置的三个互逆关系．

（3）引导学生概括出直线与圆相切的判定定理，帮助学生搞清该定理的条件和结论，尤其是两个条件要同时满足：①直线和半径垂直；②直线要过半径的外端．或者学生在叙述时常会疏漏．

（4）应给学生指出，这个判定定理还给出了圆的切线的作法．可以让学生说练课本中的“做一做”

思考

自议

经历切线的判定定理的探究过程，养成自主探索、合作探究的习惯；

 用切线的判定定理证明圆的切线，关键是要知道直线与圆有无公共点，有公共点则证明直线与半径垂直即可，简单说成：“有交点，证垂直”．

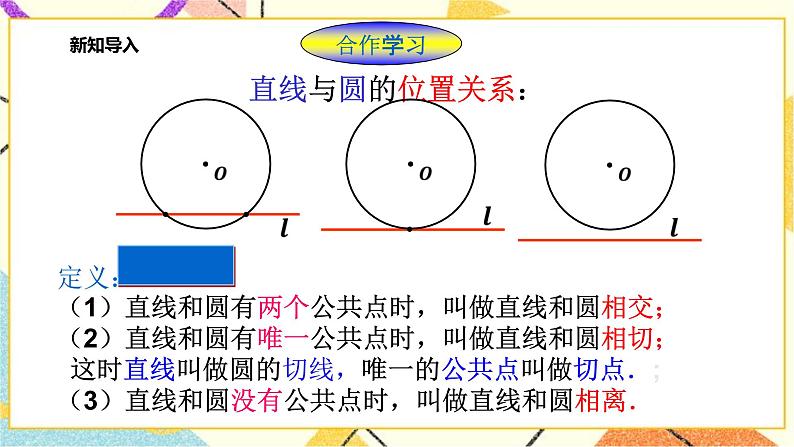
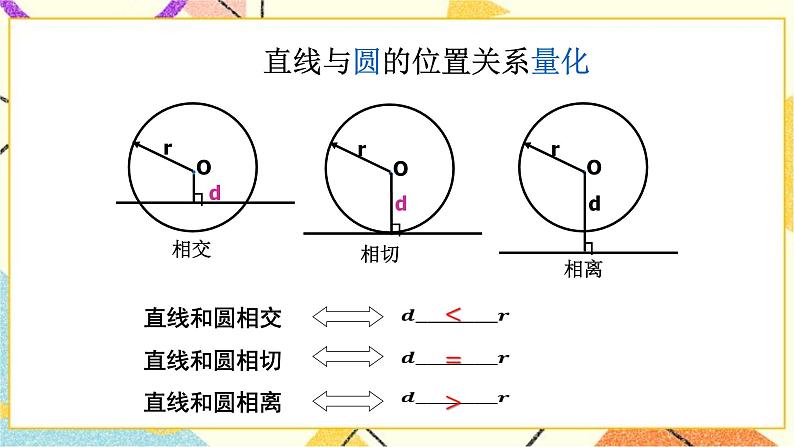
讲授新课

二、提炼概念

切线的判定方法：

① 直线与圆有唯一公共点；

② 直线到圆心的距离等于圆的半径；

③ 切线的判定定理.

三、典例精讲

【例3】已知：如图，A是⊙O外一点，AO的延长线交⊙O于点C，点B在圆上，且AB＝BC，∠A＝30°．求证：直线AB是⊙O的切线．

证明：连结OB．

∵OB＝OC，AB＝AC，∠A＝30°，

∴∠OBC＝∠C＝∠A＝30°，

∴∠AOB＝∠C＋∠OBC＝60°．

∵∠ABO＝180°－(∠AOB＋∠A)＝180°－(60°＋30°)＝90°，

∴AB⊥OB，

∴AB为⊙O的切线（经过半径的外端并且垂直这条半径的直线是圆的切线）．

此例是切线的判定方法及时得到巩固，教学时可按照下列步骤分析启发：

（1）从要求证的结论出发考虑问题，根据直线与圆相切的判定定理应怎样添加辅助线？

（2）连接OB后，要证明AB与圆O相切就要证明AB⊥OB，那么只需要证明∠ABO＝90°．

（3）从已知出发考虑问题，由AB＝BC，∠C＝30°，可以推出什么呢？得∠A＝30°后，应再说明什么？∠AOB与∠C有什么关系？

完成例3以后，还可以要求学生想一想，说明∠ABO＝90°，还有什么方法？比如，

∠ABO＝∠ABC＝∠OBC＝120°－30°＝90°．

连接圆心和切点的半径是一条常用的辅助线，小结时应予以强调．

【例4】如图，台风中心P（100，200）沿北偏东30°方向移动，受台风影响区域的半径为200km．那么下列城市A（200，380），B（600，480），C（550，300），D（370，540）中，哪些受到这次台风的影响，哪些不受到这次台风的影响？

解：如图，在坐标系中画出以点P（100，200）为圆心，以200为半径的⊙P，再在点P处画出北偏东30°方向的方向线，作垂直于方向线的⊙P的直径HK，分别过点H，K作⊙P的切线l1，l2，则l1∥l2．

因为台风圈在两条平行线l1，l2，之间移动，点A，D落在切线l1，l2，之间，所以受到这次台风的影响；而点B，C不在切线l1，l2，之间，所以不受到这次台风的影响．

解决此题的关键是确定台风圈所扫过的范围，可作如下启发：

（1）回顾课本第38页，做一做过直径两端的两条切线有何关系？

（2）过于台风圈，⊙P运动方向垂直的直径HK两端的两条切线l1，l2与台风圈运动方向有何关系？

（3）⊙P在移动过程中与直线l1，直线l2始终有这样的关系？现在你能确定台风圈扫过的范围了吗？

1.有交点，连半径，证垂直

变式1 直线AB经过⊙O上的点C，并且OA=OB，CA=CB.

求证:直线AB是⊙O的切线.

2.无交点，作垂线，证半径

变式2 如图，在Rt△ABC中，∠ACB=90°，AO是△ABC 的角平分线.以O为圆心，OC为半径作⊙O.

求证：AB是⊙O的切线.

如果直线与圆有公共点，则连结该点和圆心，证明直线垂直于经过这点的半径，即作半径、证垂直．

判定一条直线是否为圆的切线主要有三种方法：

(1)利用定义；

(2)根据圆心到直线的距离等于圆的半径；

(3)经过半径外端并且垂直这条半径的直线是圆的切线．

课堂检测

四、巩固训练

1.下列说法正确的是(　　)

      A．与圆有公共点的直线是圆的切线

      B．圆心到直线的距离等于圆的半径的直线是圆的切线

      C．垂直于圆的半径的直线是圆的切线

      D．经过圆的半径外端的直线是圆的切线

B

2．如图，△ABC内接于⊙O，AB为直径，过点A作直线EF，要使得EF是⊙O的切线，还需添加的条件是(只需写出三种)：①__________或②______ _______或③________________________.

OA⊥EF，∠FAC=∠B，∠BAC＋∠FAC＝90°

3．如图所示，以线段AB为直径的⊙O交线段AC于点E，点M是的中点，OM交AC于点D，∠BOE＝60°，cos  C＝，BC＝2.

(1)求∠A的度数；

(2)求证：BC是⊙O的切线；

(3)求MD的长度．

解：(1)∵OA＝OE.∴∠A＝∠OEA.

∵∠BOE＝60°，∴∠A＝∠BOE＝30°.

(2)证明：在△ABC中，∵cos C＝，∴∠C＝60°.

又∵∠A＝30°，∴∠ABC＝90°，∴AB⊥BC，

∴BC是⊙O的切线．

(3)∵点M是的中点，∴OM⊥AE.

在Rt△ABC中，∵BC＝2，

∴AB＝BC·tan 60°＝2×＝6，

∴OA＝＝3，∴OD＝OA＝，

∴MD＝OM－OD＝OA－OD＝.

课堂小结

1.切线的判定定理:

经过半径的外端并且垂直这条半径的直线是圆的切线.

2.切线的判定方法：

① 直线与圆有唯一公共点；

② 直线到圆心的距离等于圆的半径；

③ 切线的判定定理.