浙教版九年级下册2.1 直线和圆的位置关系优秀备课作业课件ppt

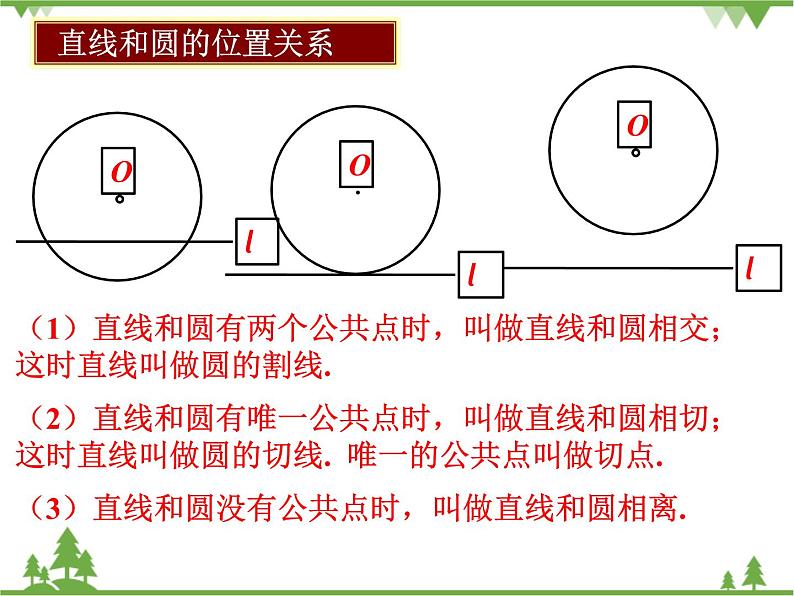
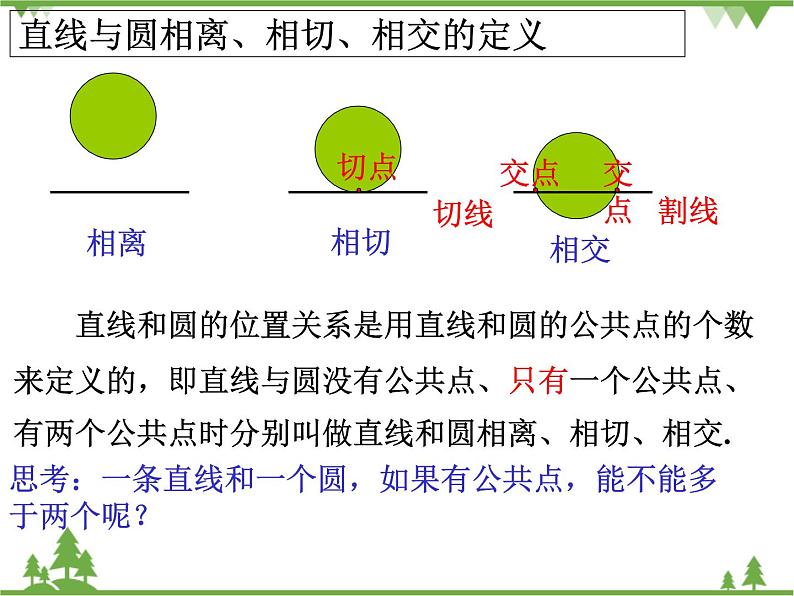
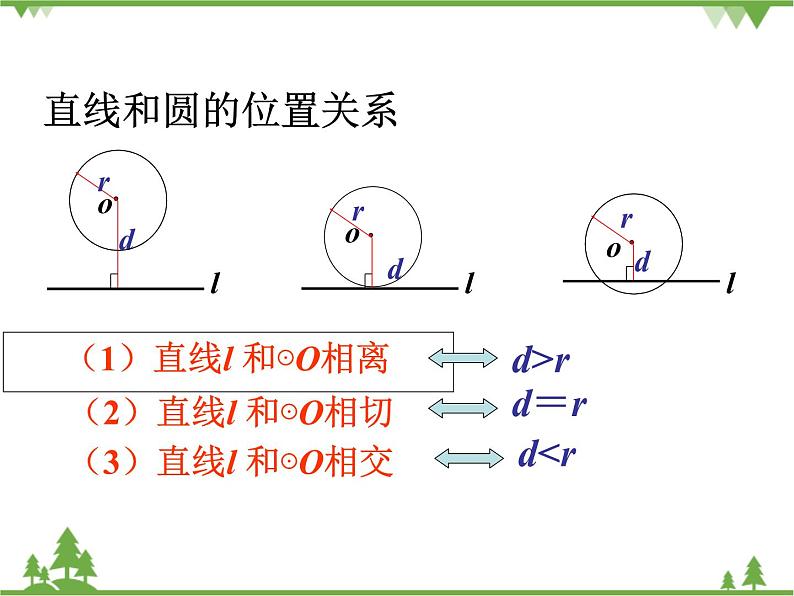
第2章   直线与圆的位置关系

2.1   直线与圆的位置关系（第1课时）

一、单选题

1．如图，为的一个内接三角形，过点作的切线与的延长线交于点．已知，则等于（    ）

A．17° B．27° C．32° D．22°

【答案】D

【分析】

连接OB，利用圆周角定理求得∠AOB，再根据切线性质证得∠OBP=90°，利用直角三角形的两锐角互余即可求解．

【详解】

解：连接OB，

∵∠ACB=34°，

∴∠AOB=2∠ACB=68°，

∵PB为的切线，

∴OB⊥PB，即∠OBP=90°,

∴∠P=90°﹣∠AOB=22°，

故选：D．

【点睛】

本题考查了切线的性质、圆周角定理、直角三角形的两锐角互余，熟练掌握切线的性质和圆周角定理是解答的关键．

2．在中，，以点为圆心，为半径作圆．若与边只有一个公共点，则的取值范围是（    ）

A． B． C．或 D．或

【答案】D

【分析】

先用勾股定理计算线段的长，分两种讨论：若与斜边相切时，通过等积法计算的面积，可求得半径的长；若，圆与边也只有一个公共点，据此解题即可.

【详解】

如图，过点作于点．

，．

①如果以点为圆心，为半径的圆与斜边相切，则．此时．

②当时，圆与边也只有一个公共点．

综上，或．

故选D．

【点睛】

本题考查圆与直线的位置关、勾股定理、三角形的面积公式等，其中涉及分类讨论的数学思想，考点知识综合性较强，难度适中，作出适当的辅助线是解题关键.

3．如图，过上一点P作的切线，与直径AB的延长线交于点C，点D是上的一点，且，则的度数为（    ）

A． B． C． D．

【答案】C

【分析】

连接OP,由圆周角定理可得∠BOP的度数,由切线性质可得∠CPO的度数,即可算出∠C的度数．

【详解】

如图所示,连接OP,则∠CPO=90°．

∵∠BDP=27°,

∴∠BOP=54°,

∴∠C=180°－90°－54°=36°．

故选C．

【点睛】

本题考查圆周角定理和切线性质,关键在于根据题意作出合理的辅助线,同时利用圆周角定理和切线性质进行角度转换．

4．如图，OA交⊙O于点B，AD切⊙O于点D，点C在⊙O上．若∠A＝40°，则∠C为（　　）

A．20° B．25° C．30° D．35°

【答案】B

【分析】

根据切线的性质得到∠ODA＝90°，根据直角三角形的性质求出∠DOA，根据圆周角定理计算即可．

【详解】

解：∵切于点

∴

∴

∵

∴

∴

故选：B

【点睛】

本题考查了切线的性质：圆心与切点的连线垂直切线、圆周角定理以及直角三角形两锐角互余的性质，结合图形认真推导即可得解．

5．如图，AB是⊙O的弦，AC与⊙O相切于点A，连接OA，OB，若∠O＝130°，则∠BAC的度数是（　　）

A．60° B．65° C．70° D．75°

【答案】B

【分析】

利用切线的性质及等腰三角形的性质求出∠OAC及∠OAB即可解决问题．

【详解】

解：∵AC与⊙O相切于点A，

∴AC⊥OA，

∴∠OAC＝90°，

∵OA＝OB，

∴∠OAB＝∠OBA．

∵∠O＝130°，

∴∠OAB＝＝25°，

∴∠BAC＝∠OAC﹣∠OAB＝90°﹣25°＝65°．

故选：B．

【点睛】

本题考查的是切线的性质，等腰三角形的性质，三角形的内角和定理，掌握以上知识是解题的关键．

6．下列说法正确的是（    ）

A．与圆有公共点的直线是圆的切线 B．到圆心的距离等于圆的半径的直线是圆的切线

C．垂直于圆的半径的直线是圆的切线 D．过圆的半径外端的直线是圆的切线

【答案】B

【分析】

根据切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线，可判定C、D错误；由切线的定义：到圆心距离等于圆的半径的直线是圆的切线，可判定A错误，B正确．注意排除法在解选择题中的应用．

【详解】

解：A、与圆只有一个交点的直线是圆的切线，故本选项错误；
B、到圆心距离等于圆的半径的直线是圆的切线，故本选项正确；
C、经过半径的外端且垂直于这条半径的直线是圆的切线，故本选项错误；
D、经过半径的外端且垂直于这条半径的直线是圆的切线，故本选项错误．
故选：B．

【点睛】

此题考查了切线的判定．此题难度不大，注意掌握切线的判定定理与切线的定义是解此题的关键．

7．如图，交于点，切于点，点在上. 若，则为（     ）

A． B． C． D．

【答案】B

【分析】

根据切线的性质得到∠ODA=90，根据直角三角形的性质求出∠DOA，根据圆周角定理计算即可．

【详解】

∵AD切⊙O于点D，
∴OD⊥AD，
∴∠ODA=90，
∵∠A=40，
∴∠DOA=90-40=50，
由圆周角定理得，∠BCD=∠DOA=25°，
故选：B．

【点睛】

本题考查的是切线的性质、圆周角定理，掌握圆的切线垂直于经过切点的半径是解题的关键．

8．如图，AB为⊙O的切线，点A为切点，OB交⊙O于点C，点D在⊙O上，连接AD、CD、OA，若∠ADC＝40°，则∠ABO的度数为（      ）

A．10° B．20° C．30° D．40°

【答案】A

【分析】

根据切线的性质和圆周角定理即可得到结论．

【详解】

∵AB为圆O的切线，

∴AB⊥OA，即∠OAB＝90°，

∵∠ADC＝40°，

∴∠AOB＝2∠ADC＝80°，

∴∠ABO＝90°−80°＝10°．

故选：A．

【点睛】

此题考查了切线的性质，以及圆周角定理，熟练掌握切线的性质是解本题的关键．

二、填空题

9．若的半径为，点到直线的距离为，且直线与相交，则______ ．（填“>”或“<”或“=”）

【答案】

【分析】

根据直线与圆相交得到圆心到直线的距离小于半径．

【详解】

解：∵直线与相交，

∴圆心到直线的距离小于半径，即．

故答案是：<．

【点睛】

本题考查圆与直线的位置关系，解题的关键是掌握圆与直线相交的性质．

10．如图，、分别切于点、，点是上一点，且，则________度．

【答案】

【分析】

由圆周角定理知可知∠AOB=2∠E=120°，PA、PB分别切⊙O于点A、B，利用切线的性质可知∠OAP=∠OBP=90°，根据四边形内角和可求得∠P=180°-∠AOB=60°．

【详解】

解： ∵∠AOB=2∠E=120°，

 ∴∠OAP=∠OBP=90°，

 ∴∠P=180°-∠AOB=60°．

故答案为：

【点睛】

本题利用了圆周角定理，切线的性质，四边形的内角和为360度求解．

11．如图，AB是⊙O的直径，AC是⊙O的切线，连接OC与⊙O相交于点D，连接BD，∠C＝40°，若点P为优弧上的动点，连接PA、PD，则∠APD的大小是_____度．

【答案】25

【分析】

先根据圆的切线的性质得出，再根据直角三角形的性质可得，然后根据圆周角定理即可得．

【详解】

如图，连接PA、PD

∵AC是⊙O的切线

∴，即

∵

∴

∴

故答案为：25．

【点睛】

本题考查了圆的切线的性质、圆周角定理等知识点，熟记圆周角定理是解题关键．

12．已知矩形ABCD，对角线AC与BD相交于点O，AB＝6，BC＝8，分别以点O、D为圆心画圆，如果⊙O与直线AD相交、与直线CD相离，且⊙D与⊙O内切，那么⊙D的半径长r的取值范围是______．

【答案】8＜r＜9

【分析】

根据圆与圆的位置关系即可求出答案．

【详解】

解：设⊙O的半径为r1，⊙D半径为r，

由⊙O与直线AD相交、与直线CD相离可知：3＜r1＜4，

由题意可知：r＞r1，否则⊙D与⊙O不能内切，

∵OD＝AC＝5，

∴圆心距d＝5，

∴d＝r﹣r1，

∴r＝5+r1，

∴8＜r＜9，

故答案为：8＜r＜9．

【点睛】

考查了圆与圆的位置关系，解题关键是正确运用圆心距与两圆的半径的数量关系．

13．如图，AB是⊙Ｏ的直径，BC与⊙Ｏ相切于点B，AC交⊙Ｏ于点D，若∠ACB=50°，则∠BOD=______度．

【答案】80

【分析】

根据切线的性质得到∠ABC=90°，根据直角三角形的性质求出∠A，根据圆周角定理计算即可．

【详解】

解：∵BC是⊙O的切线，
∴∠ABC=90°，
∴∠A=90°-∠ACB=40°，
由圆周角定理得，∠BOD=2∠A=80°.

【点睛】

本题考查的是切线的性质、圆周角定理，掌握圆的切线垂直于经过切点的半径是解题的关键．

14．如图，的半径垂直于弦，过点作的切线交的延长线于点，连结，若，则等于__________度.

【答案】28

【分析】

连接 利用切线的性质求解 利用圆周角定理可得答案．

【详解】

解：连接

为的切线，

故答案为：

【点睛】

本题考查的是圆的基本性质：圆周角定理，圆的切线的性质，掌握以上的知识是解题的关键．

三、解答题

15．如图，已知△ABC内接于⊙O，点D在OC的延长线上，CD＝CB，∠D＝∠A

（1）求证：BD是⊙O的切线；

（2）若BC＝2，求BD的长．

【答案】（1）见解析；（2）BD＝2

【分析】

（1）由等腰三角形的性质得出∠CBD+∠OBC＝90°，则∠OBD＝90°，可得出结论；

（2）证明△OBC为等边三角形，得出∠BOC＝60°，根据直角三角形的性质可得出答案．

【详解】

（1）证明：∵OB＝OC，

∴∠OBC＝∠OCB，

∴∠BOC+2∠OBC＝180°，

∵∠BOC＝2∠A，

∴∠A+∠OBC＝90°，

又∵BC＝CD，

∴∠D＝∠CBD，

∵∠A＝∠D，

∴∠CBD+∠OBC＝90°，

∴∠OBD＝90°，

∴OB⊥BD，

∴BD是⊙O的切线；

（2）解：∵∠OBD＝90°，∠D＝∠CBD，

∴∠OBC＝∠BOC，

∴OC＝BC，

又∵OB＝OC，

∴△OBC为等边三角形，

∴∠BOC＝60°，

∵BC＝2，

∴OB＝2，

∴BD＝2．

【点睛】

本题考查切线的判定，等腰三角形的性质，圆周角定理，直角三角形的性质，等边三角形的判定与性质，熟练掌握切线的判定是解题的关键．

16．如图，AB与⊙O相切于点B，AO交⊙O于点C，AO的延长线交⊙O于点D，E是弧BCD上不与B，D重合的点，∠A=30°．

（1）求∠BED的度数；

（2）点F在AB的延长线上，且DF与⊙O相切于点D，求证：BF=AB．

【答案】（1）60°；（2）见解析．

【分析】

（1）如图，连接 利用圆的切线的性质，求解 利用圆周角定理可得答案；

（2）由圆的性质求解可得 结合切线的性质证明为等边三角形，从而可得答案．

【详解】

解：（1）如图，连接

为的切线，

（2）

为的切线，

为等边三角形，

【点睛】

本题考查的是圆的切线的性质，圆周角定理，等腰三角形的性质与判定，等边三角形的判定与性质，掌握以上知识是解题的关键．

17．如图，⊙O的直径为AB，点C在圆周上(异于点A，B)，AD⊥CD．

(1)若BC＝3，AB＝5，求AC的长；

(2)若AC是∠DAB的平分线，求证：直线CD是⊙O的切线．

【答案】(1) AC=4；(2)详见解析.

【分析】

（1）首先根据直径所对的圆周角为直角得到直角三角形，然后利用勾股定理求得AC的长即可；
（2）连接OC，证OC⊥CD即可；利用角平分线的性质和等边对等角，可证得∠OCA=∠CAD，即可得到OC∥AD，由于AD⊥CD，那么OC⊥CD，由此得证．

【详解】

解：（1）∵AB是⊙O直径，C在⊙O上，

∴∠ACB＝90°，

又∵BC＝3，AB＝5，

∴由勾股定理得AC＝4；

（2）证明：连接OC

∵AC是∠DAB的角平分线，

∴∠DAC＝∠BAC，

又∵AD⊥DC，

∴∠ADC＝∠ACB＝90°，

∴△ADC∽△ACB，

∴∠DCA＝∠CBA，

又∵OA＝OC，

∴∠OAC＝∠OCA，

∵∠OAC+∠OBC＝90°，

∴∠OCA+∠ACD＝∠OCD＝90°，

∴DC是⊙O的切线．

【点睛】

本题考查的知识点是切线的判定方法，解题关键是熟记要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．

18．如图，OA、OB是⊙的半径，，为延长线上一点，切⊙于点，为与的交点，连结．已知=5，求线段的长．

【答案】5

【分析】

利用切线的性质与，证明∠DEC=∠ADC，从而可得答案．

【详解】

解：∵切O于点Ｄ，

∴∠ODC=；

又∵OA⊥OC，即∠AOC=，

∴∠A+∠AEO=，∠ADO+∠ADC=

∵OA=OD，

∴∠A=∠ADO，

∴∠ADC=∠AEO；

又∵∠AEO=∠DEC，

∴∠DEC=∠ADC，

∴CD=CE，

∵CE=5，

∴CD=5．

【点睛】

本题考查的是圆的切线的性质，等腰三角形的判定，直角三角形的两锐角互余，掌握以上知识是解题的关键．

19．如图，在△ABC中，AB＝AC，O是边AC上的点，以OC为半径的圆分别交边BC、AC于点D、E，过点D作DF⊥AB于点F．

（1）求证：直线DF是⊙O的切线；

（2）若OC＝1，∠A＝45°，求劣弧DE的长．

【答案】（1）详见解析；（2）π．

【分析】

（1）连结OD，根据等腰三角形的性质得到OD∥AB，根据平行线的性质得到∠ODF＝90°，根据切线的判定定理证明；

（2）根据平行线的性质得到∠AOD＝180°﹣45°＝135°，根据弧长公式计算即可．

【详解】

证明：如图，连结OD，

∵AB＝AC，

∴∠B＝∠ACB，

∵OC＝OD，

∴∠ODC＝∠ACB，

∴∠B＝∠ODC，

∴OD∥AB，

∵DF⊥AB，

∴∠ODF＝∠BFD＝90°，

∵OD为半径，

∴直线DF是⊙O的切线；

（2）解：∵∠A＝45°，OD∥AB，

∴∠AOD＝180°﹣45°＝135°，

∴劣弧DE的长为．

【点睛】

本题主要考查了切线的判定及弧长的计算，熟练掌握切线的判定定理及弧长的计算公式是解题的关键.

20．己知:如图，在平面直角坐标系中，直线与轴、轴分别交于两点，是直线上一动点，⊙的半径为2．

（1）判断原点与⊙的位置关系，并说明理由；

（2）当⊙与轴相切时，求出切点的坐标．

【答案】（1）外部，理由见解析；（2）或 ．

【分析】

（1）先求出OA，OB，进而根据三角形的面积公式求出到直线的距离，即可得出结论；

（2）首先求得当⊙P与x轴相切时，且位于x轴下方时，点D的坐标，然后利用对称性可以求得当⊙P与x轴相切时，且位于x轴上方时，点D的坐标．

【详解】

解（1）令x=0，=

∴，

令y=0，=0，解得x=3

∴

∴AO=3，OB=

，∠ABO＝30

过作D⊥AB,

设到直线的距离为，

∴d==

∴原点在的外部

（2）如图，当⊙P与x轴相切时，且位于x轴下方时，设切点为D，

在PD⊥x轴，

∴PD∥y轴，

∴∠APD＝∠ABO＝30，

∴在Rt△DAP中，AD＝DP•tan∠DPA＝2×tan30＝，

∴OD＝OA−AD＝3-，

∴此时点D的坐标为：（3-，0）；

当⊙P与x轴相切时，且位于x轴上方时，根据对称性可以求得此时切点的坐标为：（3+，0）；

综上可得：当⊙P与x轴相切时，切点的坐标为： 或 ．

【点睛】

此题考查了和圆有关的综合题，用到的知识点有一次函数图象上点的坐标的性质、切线的性质以及三角函数等知识．注意准确作出辅助线，注意分类讨论思想的应用．