




初中数学人教版七年级下册7.2.2用坐标表示平移优质课件ppt
展开(2)经过平移后,对应点所连的线段 平行且相等;
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
(1)平移不改变图形的形状和大小,只改变形图 形的位置.
议一议 在平面直角坐标系中,一个点沿x 轴方向平移a(a>0)个单位长度后的坐标是什么?
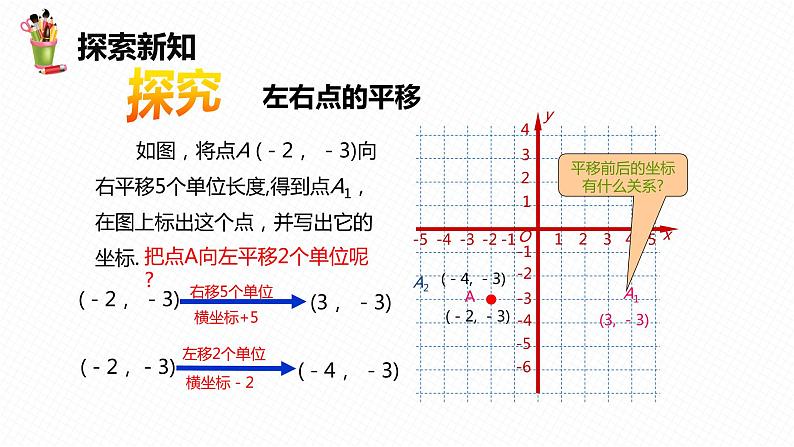
如图,将点A (-2, -3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向左平移2个单位呢?
平移前后的坐标有什么关系?
(1)点(x, y )向左平移a (a>0)个单位⇔平移后的坐标为 (x-a, y );(2)点(x, y )向右平移a (a>0)个单位⇔平移后的坐标为 (x+a, y );
议一议 在平面直角坐标系中,一个点沿y 轴方向平移a(a>0)个单位长度后的点的坐标是什么?
如图,将点A(-2, -3)向上平移6个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向下平移4个单位呢?
(1)点(x, y )向上平移a (a>0)个单位⇔平移后的坐标为 (x,y+a );(2)点(x, y )向下平移a (a>0)个单位⇔平移后的坐标为 (x, y-a ).
议一议 在平面直角坐标系中,一个点沿x 轴方向平移a (a>0)个单位长度,再沿y 轴方向平移b (b>0)个单位长度,得到点的坐标是什么?
如图,将点A(-2, -3)向右平移5个单位长度,得到点A1,再向上平移6个单位,得到点A2,在图上标出这个点,并写出它的坐标.
(1)点(x, y )向左平移a (a>0)个单位,再向上平移 b (b>0)个单位⇔平移后的坐标为(x-a, y+b );(2)点(x, y )向右平移a (a>0)个单位,再向下平移 a (a>0)个单位⇔平移后的坐标为 (x+a, y-b );
在平面直角坐标系中,有一点(1,3),要使它平移到点(-2,-2),应怎样平移?说出平移的路线.
温馨提示:点的斜向平移,可以通过点的左右和上下移动共同来完成千万不要走斜线哦
知平移求坐标口诀:左右平移,横坐标左减右加;上下平移,纵坐标上加下减.
点P (-2,-3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )A. (-3,0) B. (-1,6) C. (-3,-6) D. (-1,0)
根据平移规律点P (-2,-3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为(-3,0),故选A.
(1)直接根据平移方向与距离,结合已知点的坐标,简 单计算即可.(2)知平移求坐标口诀:左右平移,横坐标左减右加; 上下平移,纵坐标上加下减.
如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N 的坐标为( )A.(2,-1) B.(2,3)C.(0,1) D.(4,1)
在平面直角坐标系中,将点P (3,2)向右平移2个单位长度,所得到的点的坐标是( )A.(1,2) B.(3,0) C.(3,4) D.(5,2)
若将点A (1,3)向左平移2个单位长度,再向下平移4个单位长度得到点B,则点B 的坐标为( )A.(-2,-1) B.(-1,0)C.(-1,-1) D.(-2,0)
探究如图,正方形ABCD四个顶点的坐标分别是A (-2,4),B (-2, 3),C (-1,3),D (-1,4),将正方形ABCD 向下平移7个单位长度,再向右平移8个单位长度,两次平移
后四个顶点相应变为点E,F,G,H,它们的坐标分别是什么?如果直接平移正方形ABCD,使点A 移到点E,它和我们前面得到的正方形位置相同吗?可求出点E,F,G,H 的坐标分别是(6,-3),(6,-4),(7,-4),(7,-3).如果直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同(如图).
一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到. 对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
思考(1)如果将这个问题中的“横坐标都减去6”“纵坐标 都减去5”相应地变为“横坐标都加3”“纵坐标都 加2”,分别能得出什么结论?画出得到的图形.(2)如果将三角形ABC 三个顶点的横坐标都减去6,同 时纵坐标都减去5,能得到什么结论?画出得到的 图形.
一般地,在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a 个单位 长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a 个单位长度.
如图,三角形ABC 三个顶点的坐标分别是A (4,3),B (3,1),C (1,2).
(1)将三角形ABC 三个顶点的横坐标都减去6,纵坐标不变, 分别得到A1,B1,C1 ,依次连接A1,B1,C1各点, 所得三角形A1B1C1与三角形 ABC 的大小、形状和位置有 什么关系? (2)将三角形ABC 三个顶点的纵坐标都减去5,横坐标不变, 分别得到 点A2,B2,C2,依次连接A2, B2,C2各点, 所得三角形A2B2C2与三角形 ABC 的大小、形状和位置 有什么关系?
如图,所得三角形A1B1C1与三角形ABC 的大小、形状完 全相同,三角形A1B1C1可以看作将三角形ABC 向左平移6个单位长度得到. 类似地,三角形A2B2C2与三角形ABC 的大小、形状完全相同,它可以看作 将三角形ABC 向下平移5个单位长度得到.
从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移;横坐标的变化决定图形左右平移,纵坐标的变化决定图形上下平移.
如图,将平行四边形ABCD 向左平移2个单位长度,然后再向上平移3个单位长度,可以得到平行四边形A′B′C′D′,画出平移后的图形,并指出其各个顶点的坐标.
图略.A ′点的坐标为(-3,1),B ′点的坐标为(1,1),C ′点的坐标为(2,4),D ′点的坐标为(-2,4).
在平面直角坐标系xOy 中,线段AB 的两个端点坐标分别为A (-1,-1),B (1,2),平移线段AB,得到线段A′B ′,已知点A′的坐标为(3,-1),则点B ′的坐标为( )A.(4,2) B.(5,2) C.(6,2) D.(5,3)
如图,将△PQR 向右平移2个单位长度,再向下平移3个单位长度,则顶点P 平移后的坐标是( )A.(-2,-4) B.(-2,4)C.(2,-3) D.(-1,-3)
如图,若图①中点P 的坐标为 ,则它在图②中的对应点P1的坐标为( )A.(3,2) B. C. D.
如图,线段AB 经过平移得到线段A′B ′,其中点A,B 的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P (a,b),则点P 在A′B ′上的对应点P ′的坐标为( )A.(a-2,b+3) B.(a-2,b-3)C.(a+2,b+3) D.(a+2,b-3)
若一个四边形的其中一顶点P 在平移的过程中,坐标变化为P (x,y ) →P ′(x+3,y ),则该四边形的平移情况是( )A.向左平移3个单位长度 B.向右平移3个单位长度C.向上平移3个单位长度 D.向下平移3个单位长度
如图,在平面直角坐标系中,三角形ABC 的顶点都在格点上,其中,C点坐标为(1,2).(1)写出点A,B 的坐标: A(____,____), B(____,____);
(2)将三角形ABC 先向左平移2个单位长度,再向上平移1个单 位长度,得到三角形A′B′C ′,则三角形A′B′C ′的三个顶点坐 标分别是A′(____,____),B ′(____,____),C ′(____,____);(3)三角形ABC 的面积为________.
已知坐标平面内的点A (-2,5),如果将坐标系先向左平移3个单位长度,再向上平移4个单位长度,则点A在新坐标系中的坐标为________.
易错点:混淆坐标系的平移和点的平移而出错
在平面直角坐标系中,将点A (x,y )向左平移5个单位长度,再向上平移3个单位长度后与点B (-3,2)重合,则点A 的坐标是( )A.(2,5) B.(-8,5)C.(-8,-1) D.(2,-1)
如图为某动物园的示意图.(图中小正方形的边长代表 1个单位长度) (1)以虎山为原点,水平向右为x 轴正方向、铅直向上 为y 轴正方向在图中建立平面直角坐标系,并写出 各景点的坐标. (2)若以猴园为原点,水平向右为x 轴正方向、铅直向 上为y 轴正方向建立平面直角 坐标系,写出各景点的坐标. (3)比较(1)、(2)中各景点的 坐标,你发现了什么规律?
(1)如图①,由图可得虎山(0,0)、熊猫馆(3,2)、鸟岛 (-1,3)、狮子馆(-2,-2)、猴园(3,-1).(2)如图②,由图可得虎山(-3,1)、熊猫馆(0,3)、鸟 岛(-4,4)、狮子馆(-5,-1)、猴园(0,0).(3)(2)中各景点的坐标与(1)中的相比,横坐标减小3, 纵坐标增加1.
如图,长方形ABCD 在坐标平面内,点A 的坐标是 ( ,1),且边AB,CD 与x 轴平行,边AD,BC 与y 轴平行,AB=4,AD=2. (1)求B,C,D 三点的坐标. (2)怎样平移,才能使A 点与原点重合?
(1)因为A ( ,1),AB=4,AD=2, 所以BC 到y 轴的距离为4+ ,CD 到x 轴的距离为 2+1=3. 所以B (4+ ,1),C (4+ ,3),D ( ,3).(2)先向下平移1个单位长度,再向左平移 个单位长 度(或先向左平移 个单位长度,再向下平移1个 单位长度).
在平面直角坐标系中,三角形ABC 三个顶点的坐标 分别是A(-4,-4),B(-2,-3),C(-3,-1). (1)将三角形ABC 三个顶点的横坐标都加上5,纵坐标不变, 分别得到点A1,B1,C1,依次连接A1,B1,C1各点, 所得三角形A1B1C1与三角形ABC 在大小、形状和位置上 有什么关系? (2)将三角形ABC 三个顶点的纵坐标都加上4,横坐标不变, 分别得到点A2,B2,C2,依次连接A2,B2,C2各点,所得 三角形A2B2C2与三角形ABC 在大小、形状和位置上有什么关系?
平移后的图形如图所示.(1)所得三角形A1B1C1与三角形ABC 的大 小、形状完全相同,三角形A1B1C1可 以看作是将三角形ABC 向右平移5个 单位长度得到的.(2)所得三角形A2B2C2与三角形ABC 的大小、形状完全相 同,三角形A2B2C2可以看作是将三角形ABC 向上平移 4个单位长度得到的.
在平面直角坐标系中,三角形ABC 的三个顶点的位置如图所示,点A′的坐标是(-2,2),现将三角形ABC 平移,使点A 变换为点A′,点B ′,C ′分别是B,C 的对应点. (1)请画出平移后的三角形A ′B ′C ′(不写画法),并直接写出B ′,C ′ 的坐标;(2)若三角形ABC 内部一点P 的坐标为(a,b),则点P 的对应点P ′ 的坐标是 .
已知三角形ABC 在平面直角坐标系中的位置如图所 示,将三角形ABC 先向下平移5个单位长度,再向左 平移2个单位长度,求平移后C 点的对应点的坐标和 三角形ABC 所扫过部分的面积.
如图,平移后C 点的对应点的坐标为(1,-2).三角形ABC 所扫过部分的面积=S三角形ABC+S长方形ABB′A′+S三角形A″A′C″=3×2× +3×5+ ×2×2=3+15+2=20.
如图,有8×8的正方形网格,按要求操作并计算. (1)在8×8的正方形网格中建立平面直角坐标系, 使点A 的坐标为(2,4),点B 的坐标为(4,2); (2)将点A 向下平移5个单位长度,再关于y 轴对称 得到点C,求点C 的坐标; (3)画出三角形ABC,并求其面积.
(1)如图所示.(2)点A向下平移5个单位长度得到点(2,-1),其关于 y 轴对称的点C 的坐标为(-2,-1).(3)如图,S三角形ABC=S长方形CDEF-S三角形BCD-S三角形AFC -S三角形ABE=5×6- ×6×3- ×4×5- ×2× 2=9.
点的平移与点的坐标变化规律:左、右平移,横变纵不变,“右加左减”;上、下平移,纵变横不变,“上加下减”.
初中数学人教版七年级下册7.1.2平面直角坐标系完整版ppt课件: 这是一份初中数学人教版七年级下册7.1.2平面直角坐标系完整版ppt课件,共33页。PPT课件主要包含了知识回顾,学习目标,新知探究,小强家,小敏家,跟踪训练,随堂练习,用方向和距离表示,表示地理位置,课堂小结等内容,欢迎下载使用。
人教版七年级下册7.2.1用坐标表示地理位置优质ppt课件: 这是一份人教版七年级下册7.2.1用坐标表示地理位置优质ppt课件,共41页。PPT课件主要包含了课前导入,新课精讲,学以致用,课堂小结,情景导入,探索新知,知识点,用坐标表示地理位置,典题精讲,易错提醒等内容,欢迎下载使用。
初中数学人教版七年级下册7.2.1用坐标表示地理位置课文内容ppt课件: 这是一份初中数学人教版七年级下册7.2.1用坐标表示地理位置课文内容ppt课件,共33页。PPT课件主要包含了知识回顾,学习目标,新知探究,小强家,小敏家,跟踪训练,随堂练习,用方向和距离表示,表示地理位置,课堂小结等内容,欢迎下载使用。













