扬州中学教育集团树人学校2021-2022学年八年级3月月考数学试题（含解析）

这是一份扬州中学教育集团树人学校2021-2022学年八年级3月月考数学试题（含解析），共33页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

扬州中学教育集团树人学校2021-2022学年八年级3月月考数学试题
一、选择题（每小题3分，共24分）
1. 下列各图是选自历届冬奥会会徽中图案，其中是中心对称图形的是（ ）
A. B.
C. D.
2. 下列调查中，最适合采用普查的是（　　）
A. 对我市市民知晓“一带一盔”安全守护行动的调查
B. 为保证“神舟十三号”载人飞船成功发射，对其零部件情况进行检查
C. 对全国中学生每天参与体育锻炼情况的调查
D. 了解一批节能灯的使用寿命
3. 已知不透明的袋中只装有黑、白两种球，这些球除颜色外都相同，其中白球有2个，黑球有个，若随机地从袋子中摸出一个球，记录下颜色后，放回袋子中并摇匀，经过大量重复试验发现摸出白球的频率稳定在0.4附近，则的值为（ ）
A. 3 B. 4 C. 5 D. 6
4. 如图，在中，，，将绕点A顺时针旋转60°得到，此时点B的对应点D恰好落在BC边上，则CD的长为（ ）

A 1 B. 2 C. 3 D. 4
5. 为了了解某区八年级10000名学生的身高情况，从中抽取500名学生的身高进行统计，下列说法不正确的是（ ）
A. 10000名学生身高的全体是总体 B. 每个学生的身高是个体
C. 500名学生身高情况是总体的一个样本 D. 样本容量为10000
6. 用反证法证明“在同一个平面内，若，，则”时，应先假设（ ）
A. a不垂直于c B. a与b相交
C. a不垂直于b D. a，b都不垂直于c
7. 如图，是的边延长线上一点，连接，，，交于点，添加以下条件，不能判定四边形为平行四边形的是（　　　）

A. B. C. D.
8. 如图，已知一个矩形纸片OACB，将该纸片放置在平面直角坐标系中，点A（10，0），点B（0，6），点P为BC边上的动点，将△OBP沿OP折叠得到△ODP，连接CD、AD．则下列结论中：①当∠BOP=45°时，四边形OBPD为正方形；②当∠BOP=30°时，△OAD的面积为15；③当OD⊥AD时，BP=2．其中结论正确的有（ ）

A. 0个 B. 1个 C. 2个 D. 3个
二、填空题（（每小题3分，共30分）
9. 某学生买票去看电影《你好，李焕英》，“电影票座位号码是奇数”属于_____事件．
10. 为了调查滨湖区八年级学生期末考试数学试卷答题情况，从全区的数学试卷中随机抽取了10本没拆封的试卷作为样本，每本含试卷30份，这次抽样调查的样本容量是________．
11. 将50个数据分成5组列出频数分布表，其中第一组的频数是6，第二组与第五组的频数和为20，第三组的频率为0.2，则第四组的频数为_______.
12. 在一个不透明的布袋中，有红球、白球共20个，除颜色外其他完全相同，小明通过多次摸球试验后发现，其中摸到红球的频率稳定在50%，则随机从口袋中摸出一个是红球的概率是______．
13. 如图，将△ABC绕点A按逆时针方向旋转100°得到△ADE，连接EB，若AD∥BE，则∠DAE＝_______．

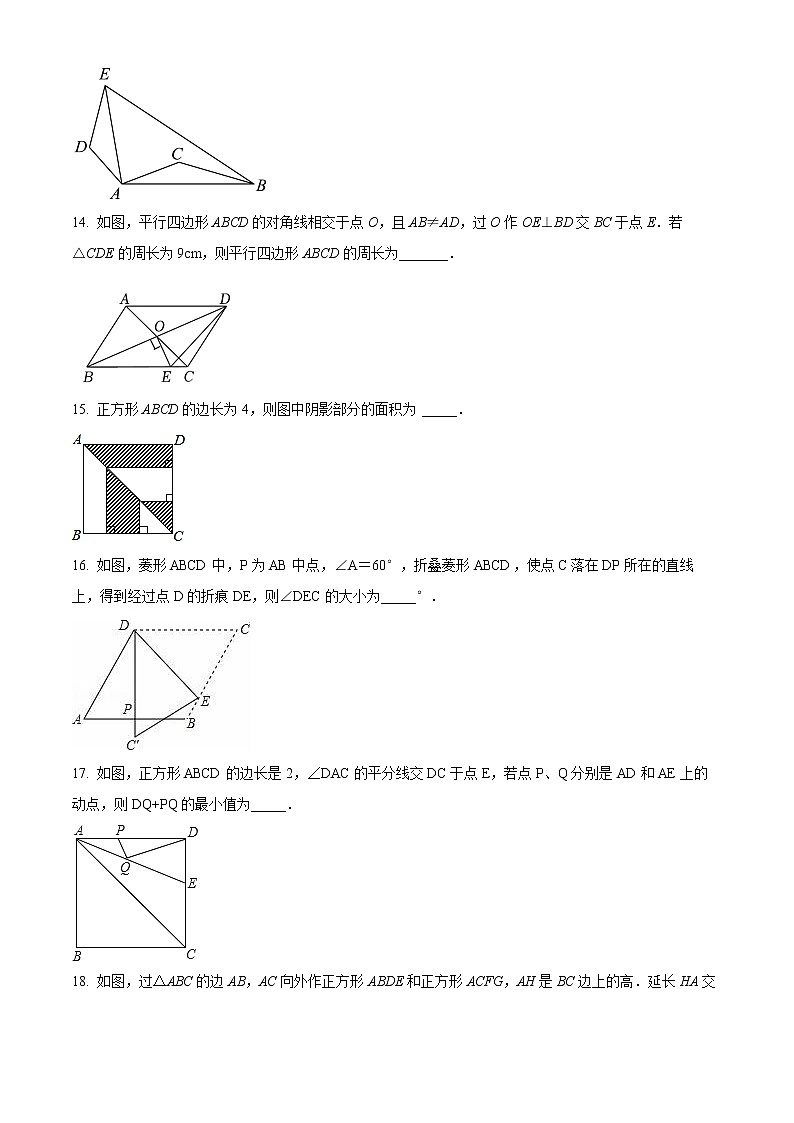
14. 如图，平行四边形ABCD的对角线相交于点O，且AB≠AD，过O作OE⊥BD交BC于点E．若△CDE的周长为9cm，则平行四边形ABCD的周长为_______．

15. 正方形ABCD的边长为4，则图中阴影部分的面积为 _____．

16. 如图，菱形ABCD中，P为AB中点，∠A＝60°，折叠菱形ABCD，使点C落在DP所在的直线上，得到经过点D的折痕DE，则∠DEC的大小为_____°．

17. 如图，正方形ABCD的边长是2，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值为_____．

18. 如图，过△ABC的边AB，AC向外作正方形ABDE和正方形ACFG，AH是BC边上的高．延长HA交EG于点I．若=7，则=_______．

三、解答题 （本大题共96分）
19. 在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，下表是活动进行中的一组统计数据：
摸球的次数n
100
200
300
500
800
1000
摸到黑球次数m
65
118
189
310
482
602
摸到黑球的频率
0.65
0.59
0.63
0.62
0.603
0.602
（1）请估计：当n很大时，摸到黑球的频率将会接近 （精确到0.1）；
（2）试估计袋子中有黑球 个；
（3）若学习小组通过实验结果，想使得在这个不透明袋子中每次摸到黑球的可能性大小为 50%，则可以在袋子中增加相同的白球 个或减少黑球 个
20. 如图，已知ΔABC的三个顶点坐标为A(−3，4)、B(−7，1)、C(−2，1)．

（1）请画出关于坐标原点的中心对称图形△，并写出点的对应点的坐标： ；
（2）将绕坐标原点顺时针旋转，直接写出点的对应点的坐标： ；
（3）请直接写出：位于第三象限且与A、B、C三个顶点构成平行四边形的D的坐标： ．
21. 为响应全面推进中小学校“社会主义核心价值观”教育年活动．某校对全校学生进行了中期检测评价，检测结果分为A（优秀）、B（良好）、C（合格）、D（不合格）四个等级．并随机抽取若干名学生的检测结果作为样本进行数据处理，制作了如下所示不完整的统计表和统计图．
等级
频数
频率
A
a
0.3
B
35
0.35
C
31
b
D
4
0.04

请根据图表提供的信息，解答下列问题：
（1）a=　 　，b=　 　；
（2）请补全条形统计图；
（3）若该校共有学生800人，据此估算，该校学生在本次检测中达到“A（优秀）”等级的学生人数为　 　人．
22. 如图，在□ABCD中，E是BC上的一点，且AB=BE，AE、DC的延长线相交于点F，∠F=62°．求∠BAE和∠D的度数．

23. 已知：如图，在□ABCD中，∠ABC、∠ADC平分线分别交AD、BC于点E、F． 求证：BEDF．

24. 如图，点C是的中点，四边形是平行四边形．
（1）求证：四边形是平行四边形；
（2）如果，求证：四边形矩形．

25. 如图，矩形ABCD中，点E在边CD上，将△BCE沿BE折叠，点C落在AD边上的点F处，过点F作FG∥CD交BE于点G，连接CG．

（1）求证：四边形CEFG是菱形；
（2）若AB=6，AD=10，求四边形CEFG的面积．
26. 邻边不相等的平行四边形纸片，剪去一个菱形，余下的一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；…依此类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图1，▱ABCD中，若AB＝1，BC＝2，则▱ABCD为1阶准菱形．
(1)猜想与计算：
邻边长分别为3和5的平行四边形是______阶准菱形；已知▱ABCD的邻边长分别为a，b(a＞b)，满足a＝8b+r，b＝5r，请写出，▱ABCD是_____阶准菱形．
(2)操作与推理：
小明为了剪去一个菱形，进行了如下操作：如图2，把▱ABCD沿BE折叠(点E在AD上)，使点A落在BC边上的点F处，得到四边形ABFE．请证明四边形ABFE是菱形．

27. 如图，在正方形ABCD中，点E、F分别在边BC、CD上，且∠EAF ＝45°，分别连接EF、BD，BD与AF、AE分别相交于点M、N．

（1）求证：EF=BE+DF．为了证明“EF=BE+DF”，小明延长CB至点G，使BG＝DF，连接AG，请画出辅助线并按小明的思路写出证明过程．
（2）若正方形ABCD的边长为6，BE=2，求DF的长．
（3）请直接写出线段BN、MN、DM三者之间的数量关系．
28. 已知，如图，为坐标原点，四边形为矩形，，，点是的中点，动点在线段上以每秒个单位长的速度由点向运动．设动点的运动时间为秒．

（1）当为何值时，四边形是平行四边形？
（2）在直线上是否存在一点，使得、、、四点为顶点的四边形是菱形？若存在，求的值，并求出点的坐标；若不存在，请说明理由．
（3）在线段上有一点，且，当运动几秒时，四边形的周长最小，并画图标出点的位置．
答案与解析
一、选择题（每小题3分，共24分）
1. 下列各图是选自历届冬奥会会徽中的图案，其中是中心对称图形的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】根据中心对称图形的概念进行判别即可．
【详解】A．不是中心对称图形，本选项不符合题意；
B．不是中心对称图形，本选项不符合题意；
C．是中心对称图形，本选项符合题意；
D．不是中心对称图形，本选项不符合题意．
故选：C．
【点睛】本题考查了中心对称图形，即在平面内，把一个图形绕某点旋转180°，如果旋转后的图形与另一个图形重合，那么这两个图形互为中心对称图形，熟练掌握知识点是解题的关键．
2. 下列调查中，最适合采用普查的是（　　）
A. 对我市市民知晓“一带一盔”安全守护行动的调查
B. 为保证“神舟十三号”载人飞船成功发射，对其零部件情况进行检查
C. 对全国中学生每天参与体育锻炼情况的调查
D. 了解一批节能灯的使用寿命
【答案】B
【解析】
【分析】根据抽样调查、全面调查的意义以及具体的问题情境进行判断即可．
【详解】解：A．对我市市民知晓“一带一盔”安全守护行动的调查，由于个体较多，又没有必要全部调查，所以宜采取抽样调查，因此选项A不符合题意；
B．为保证“神舟十三号”载人飞船成功发射，对其零部件情况进行检查，必须采取全面调查，因此选项B符合题意；
C．对全国中学生每天参与体育锻炼情况的调查，适合采用抽样调查，因此选项C不符合题意；
D．了解一批节能灯的使用寿命，适合采用抽样调查，因此选项D不符合题意；
故选：B．
【点睛】本题考查全面调查、抽样调查，理解全面调查、抽样调查的意义和适用范围是正确判断的前提．
3. 已知不透明的袋中只装有黑、白两种球，这些球除颜色外都相同，其中白球有2个，黑球有个，若随机地从袋子中摸出一个球，记录下颜色后，放回袋子中并摇匀，经过大量重复试验发现摸出白球的频率稳定在0.4附近，则的值为（ ）
A. 3 B. 4 C. 5 D. 6
【答案】A
【解析】
【分析】根据题意可得，然后进行求解即可．
【详解】解：由题意得：
，
解得：，
经检验是原方程的解；
故选A．
【点睛】本题主要考查分式方程的解法及概率，熟练掌握分式方程的解法及概率是解题的关键．
4. 如图，在中，，，将绕点A顺时针旋转60°得到，此时点B的对应点D恰好落在BC边上，则CD的长为（ ）

A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
【分析】由题意以及旋转的性质可得为等边三角形，则BD=2，故CD=BC-BD=2．
【详解】由题意以及旋转的性质知AD=AB，∠BAD=60°
∴∠ADB=∠ABD
∵∠ADB+∠ABD+∠BAD=180°
∴∠ADB=∠ABD=60°
故为等边三角形，即AB= AD =BD=2
则CD=BC-BD=4-2=2
故选：B．
【点睛】本题考查了等边三角形的判定及性质，等边三角形的三边都相等，三个内角都相等，并且每一个内角都等于，等边三角形判定的方法有：三边相等的三角形是等边三角形（定义）；三个内角都相等的三角形是等边三角形；有一个内角是60度的等腰三角形是等边三角形；两个内角为60度的三角形是等边三角形．
5. 为了了解某区八年级10000名学生的身高情况，从中抽取500名学生的身高进行统计，下列说法不正确的是（ ）
A. 10000名学生身高的全体是总体 B. 每个学生的身高是个体
C. 500名学生身高情况是总体的一个样本 D. 样本容量为10000
【答案】D
【解析】
【分析】我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对象从而找出总体、个体再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量．
【详解】解：A. 10000名学生的身高是总体，正确，故A不符合题意；
B. 每个学生的身高是个体，正确，故B不符合题意；
C. 500名学生身高情况是总体的一个样本，正确，故C不符合题意；
D. 样本容量是500，不正确，故D符合题意．
故选D．
【点睛】本题主要考查了总体、个体、样本、样本容量，解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象，总体、个体与样本的考查对象是相同的，所不同的是范围的大小；样本容量是样本中包含的个体的数目，不能带单位．总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．
6. 用反证法证明“在同一个平面内，若，，则”时，应先假设（ ）
A. a不垂直于c B. a与b相交
C. a不垂直于b D. a，b都不垂直于c
【答案】B
【解析】
【分析】反证法的步骤中，第一步是假设证明结论不成立，反面成立，所以在同一个平面内，两直线平行的反面是两直线相交．
【详解】解：反证法证明“在同一个平面内，若，，则”时，应先假设“与不平行”，而对于平面内两条直线的位置关系（除了重合）不是相交就是平行，所以“与不平行”即表示“与相交”，
故选：B．
【点睛】本题考查反证法，解题的关键是掌握反正法的步骤．尤其是要准确理解结论的反面：如果结论只有一种结果，否定一种即可；如果结论有多种情况，必须一一否定．
7. 如图，是的边延长线上一点，连接，，，交于点，添加以下条件，不能判定四边形为平行四边形的是（　　　）

A. B. C. D.
【答案】A
【解析】
【分析】根据平行线的性质得到∠AEB=∠CBF，求得∠CBF=∠BCD，求得CF=BF，同理，EF=DF，不能判定四边形BCED为平行四边形；故A错误；根据平行线的性质得到∠DEF=∠CBF，根据全等三角形的性质得到DF=CF，于是得到四边形BCED为平行四边形，故B正确；根据平行四边形的性质得到AD∥BC，AB∥CD，求得DE∥BC，∠ABD=∠CDB，推出BD∥CE，于是得到四边形BCED为平行四边形，故C正确；根据平行线的性质得到∠DEC+∠BCE=∠EDB+∠DBC=180°，推出∠BDE=∠BCE，于是得到四边形BCED为平行四边形，故D正确．
【详解】解：A、∵AE∥BC，
∴∠AEB=∠CBF，
∵∠AEB=∠BCD，
∴∠CBF=∠BCD，
∴CF=BF，
同理，EF=DF，
∴不能判定四边形BCED为平行四边形；故A错误；
∵ DE∥BC，
∴∠DEF=∠CBF，
∠DEF=∠CBF
在△DEF与△CBF中,
∴△DEF△CBF(ASA),
∴DF=CF
∵EF=BF
∴四边形BCED为平行四边形，故B正确；
∵四边形ABCD是平行四边形，
∴ .AD∥BC，AB∥CD,
∴DE∥CE，∠ABD=∠CDB,
∠ABD=∠DCE，
∴∠DCE=∠CDB，
∴BD∥CE，
∴四边形BCED为平行四边形，故C正确；
∵AEB∥C,
∴∠DEC+∠BCE=∠EDB+∠DBC=180°
∵∠AEC=∠CBD，
∴∠BDE=∠BCE，
∴四边形BCED为平行四边形，故D正确．
故选:A．
【点睛】本题考查了平行四边形的判定和性质，全等三角形的判定和性质，熟练掌握平行四边形的判定定理是解题的关键．
8. 如图，已知一个矩形纸片OACB，将该纸片放置在平面直角坐标系中，点A（10，0），点B（0，6），点P为BC边上的动点，将△OBP沿OP折叠得到△ODP，连接CD、AD．则下列结论中：①当∠BOP=45°时，四边形OBPD为正方形；②当∠BOP=30°时，△OAD的面积为15；③当OD⊥AD时，BP=2．其中结论正确的有（ ）

A. 0个 B. 1个 C. 2个 D. 3个
【答案】D
【解析】
【分析】①由矩形的性质得到∠OBC=90°，根据折叠的性质得到OB=OD，∠PDO=∠OBP=90°，∠BOP=∠DOP，推出四边形OBPD是矩形，根据正方形的判定定理即可得到四边形OBPD为正方形；故①正确；
②过D作DH⊥OA于H，得到OA=10，OB=6，根据直角三角形的性质得到DH=3，根据三角形的面积公式得到△OAD的面积为OA•DH=×3×10=15，故②正确；
③根据已知条件推出P，D，A三点共线，根据平行线性质得到∠OPB=∠POA，等量代换得到∠OPA=∠POA，求得AP=OA=10，根据勾股定理得到BP=BC-CP=10-8=2，故③正确．
【详解】解：①∵四边形OACB是矩形，
∴∠OBC=90°，
∵将△OBP沿OP折叠得到△ODP，
∴OB=OD，∠PDO=∠OBP=90°，∠BOP=∠DOP，
∵∠BOP=45°，
∴∠DOP=∠BOP=45°，
∴∠BOD=90°，
∴∠BOD=∠OBP=∠ODP=90°，
∴四边形OBPD是矩形，
∵OB=OD，
∴四边形OBPD为正方形；故①正确；
②过D作DH⊥OA于H，

∵点A（10，0），点B（0，6），
∴OA=10，OB=6，
∴OD=OB=6，∠BOP=∠DOP=30°，
∴∠DOA=30°，
∴DH=OD=3，
∴△OAD的面积为OA•DH=×3×10=15，故②正确；
③∵OD⊥AD，
∴∠ADO=90°，
∵∠ODP=∠OBP=90°，
∴∠ADP=180°，
∴P，D，A三点共线，
∵OA∥CB，
∴∠OPB=∠POA，
∵∠OPB=∠OPD，
∴∠OPA=∠POA，
∴AP=OA=10，
∵AC=6，
∴CP==8，
∴BP=BC-CP=10-8=2，故③正确；
故选：D．
【点睛】本题是四边形综合题，考查了正方形的判定和性质，矩形的性质，折叠的性质，勾股定理，三角形的面积的计算，正确的识别图形是解题的关键．
二、填空题（（每小题3分，共30分）
9. 某学生买票去看电影《你好，李焕英》，“电影票座位号码是奇数”属于_____事件．
【答案】随机
【解析】
【分析】利用随机事件的概念即可得出答案．
【详解】任意购买一张电影票，“电影票座位号码是奇数”可能发生，也可能不发生，
属于随机事件，
故答案为：随机．
【点睛】本题考查了随机事件的概念，正确理解概念是解决本题的关键．
10. 为了调查滨湖区八年级学生期末考试数学试卷答题情况，从全区的数学试卷中随机抽取了10本没拆封的试卷作为样本，每本含试卷30份，这次抽样调查的样本容量是________．
【答案】300
【解析】
【详解】从全区的数学试卷中随机抽取了10本没拆封的试卷作为样本，每本含试卷30份，
这次抽样调查的样本容量是10×30=300.
11. 将50个数据分成5组列出频数分布表，其中第一组的频数是6，第二组与第五组的频数和为20，第三组的频率为0.2，则第四组的频数为_______.
【答案】14
【解析】
【详解】根据题意，得
第三组频数是50×0.2=10，
故第四组的频数是50-6-20-10=14．
12. 在一个不透明的布袋中，有红球、白球共20个，除颜色外其他完全相同，小明通过多次摸球试验后发现，其中摸到红球的频率稳定在50%，则随机从口袋中摸出一个是红球的概率是______．
【答案】
【解析】
【分析】根据题意得出摸出红球的频率，继而根据频数=总数×频率计算即可．
【详解】解：∵小明通过多次摸球试验后发现其中摸到红球的频率稳定在50%，
∴随机从口袋中摸出一个是红球的概率是50%=．
故答案为：．
【点睛】本题比较容易，考查利用频率估计概率．大量反复试验下频率稳定值即概率．用到的知识点为：概率=所求情况数与总情况数之比．
13. 如图，将△ABC绕点A按逆时针方向旋转100°得到△ADE，连接EB，若AD∥BE，则∠DAE＝_______．

【答案】40°
【解析】
【分析】根据旋转的性质即可得到∠BAE=100°，AE=AB，则 ，再由平行线的性质即可得到∠DAE=∠AEB=40°．
【详解】解：∵将△ABC绕点A按逆时针方向旋转100°得到△ADE，
∴∠BAE=100°，AE=AB，
∴ ，
∵AD∥BE，
∴∠DAE=∠AEB=40°，
故答案为：40°．

【点睛】本题主要考查了旋转的性质，等腰三角形的性质与判定，三角形内角和定理，平行线的性质，解题的关键在于能够熟练掌握旋转的性质．
14. 如图，平行四边形ABCD的对角线相交于点O，且AB≠AD，过O作OE⊥BD交BC于点E．若△CDE的周长为9cm，则平行四边形ABCD的周长为_______．

【答案】18cm##18厘米
【解析】
【分析】由四边形ABCD是平行四边形，根据平行四边形的对角线互相平分、对边相等，即可得OB＝OD，AB＝CD，AD＝BC，又由OE⊥BD，即可得OE是BD的垂直平分线，然后根据线段垂直平分线的性质，即可得BE＝DE，又由△CDE的周长为9cm，即可求得平行四边形ABCD的周长．
【详解】解：∵四边形ABCD是平行四边形，
∴OB＝OD，AB＝CD，AD＝BC，
∵OE⊥BD，
∴BE＝DE，
∵△CDE的周长9cm，
即CD+DE+EC＝9cm，
∴平行四边形ABCD的周长为：AB+BC+CD+AD＝2（BC+CD）＝2（BE+EC+CD）＝2（DE+EC+CD）＝2×9＝18cm．
故答案为：18cm．
【点睛】本题考查了平行四边形的性质与线段垂直平分线的性质．此题难度适中，注意掌握数形结合思想与转化思想的应用．
15. 正方形ABCD的边长为4，则图中阴影部分的面积为 _____．

【答案】8
【解析】
【分析】正方形的对角线是它的一条对称轴，对应点到两边的都是垂直的，距离也都相等，左边梯形面积和右边梯形面积相等，所以图中阴影部分的面积正好为正方形面积的一半．然后列式进行计算即可得解．
【详解】解：由图形可得：
S＝×4×4＝8，
所以阴影部分的面积为8．
故答案是：8．
【点睛】本题考查正方形的性质，轴对称的性质，将阴影面积转化为三角形面积是解题的关键，学会于转化的思想思考问题．
16. 如图，菱形ABCD中，P为AB中点，∠A＝60°，折叠菱形ABCD，使点C落在DP所在的直线上，得到经过点D的折痕DE，则∠DEC的大小为_____°．

【答案】75
【解析】
【分析】连接BD，由菱形的性质及∠A=60°,得到三角形ABD为等边三角形，P为AB的中点，利用三线合一得到DP为角平分线，得到∠ADP=30°，∠ADC=120°，∠C=60°，进而求出∠PDC=90°，由折叠的性质得到∠CDE=∠PDE=45°，利用三角形的内角和定理即可求出所求角的度数．
【详解】解：如图，连接BD，
∵四边形ABCD为菱形，∠A＝60°，
∴△ABD为等边三角形，∠ADC＝120°，∠C＝60°，
∵P为AB的中点，
∴DP为∠ADB的平分线，即∠ADP＝∠BDP＝30°，
∴∠PDC＝90°，
∴由折叠的性质得到∠CDE＝∠PDE＝45°，
在△DEC中，∠DEC＝180°﹣（∠CDE+∠C）＝75°．
故答案为：75°．

【点睛】此题考查翻折变换(折叠问题)和菱形的性质，解题关键在于作辅助线．
17. 如图，正方形ABCD的边长是2，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值为_____．

【答案】.
【解析】
【详解】试题分析：过D作AE的垂线交AE于F，交AC于D′，再过D′作D′P′⊥AD，由角平分线的性质可得出D′是D关于AE的对称点，进而可知D′P′即为DQ+PQ的最小值．
作D关于AE的对称点D′，再过D′作D′P′⊥AD于P′，

∵DD′⊥AE，
∴∠AFD=∠AFD′，
∵AF=AF，∠DAE=∠CAE，
∴△DAF≌△D′AF，
∴D′是D关于AE的对称点，AD′=AD=2，
∴D′P′即为DQ+PQ的最小值，
∵四边形ABCD是正方形，
∴∠DAD′=45°，
∴AP′=P′D′，
∴在Rt△AP′D′中，
P′D′2+AP′2=AD′2，AD′2=4，
∵AP′=P′D'，
2P′D′2=AD′2，即2P′D′2=4，
∴P′D′=
，即DQ+PQ的最小值为．
考点：1.轴对称-最短路线问题；2.正方形的性质．
18. 如图，过△ABC的边AB，AC向外作正方形ABDE和正方形ACFG，AH是BC边上的高．延长HA交EG于点I．若=7，则=_______．

【答案】
【解析】
【分析】过点作于点，过点作，垂足为点，通过构造出两组全等三角形，找出关系即可解题．
【详解】解：如图，

过点作于点，过点作，垂足为点．
∴，，
∴，
∴，
在和中，
，
∴，
同理可得
则，
∴
故答案为3.5
【点睛】本题考查全等三角形的判定与性质应用，适当添加辅助线构造全等三角形是解题关键．
三、解答题 （本大题共96分）
19. 在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，下表是活动进行中的一组统计数据：
摸球的次数n
100
200
300
500
800
1000
摸到黑球的次数m
65
118
189
310
482
602
摸到黑球的频率
0.65
0.59
0.63
0.62
0.603
0.602
（1）请估计：当n很大时，摸到黑球的频率将会接近 （精确到0.1）；
（2）试估计袋子中有黑球 个；
（3）若学习小组通过实验结果，想使得在这个不透明袋子中每次摸到黑球的可能性大小为 50%，则可以在袋子中增加相同的白球 个或减少黑球 个
【答案】（1）0.6；（2）；（3）10；10．
【解析】
【分析】（1）观察表格中摸到黑球的频率可得结果；
（2）用总数乘以黑球的频率即可得到结果；
（3）根据摸到黑球的可能性大小为50%，则黑球和白球相同，据此计算即可．
【详解】解：（1）观察表格得：当n很大时，
摸到黑球的频率将会接近0.6，
故答案为：0.6；
（2）黑球有：个，
故答案为：；
（3）原来白球的数量为：50-30=20，
摸到黑球的可能性大小为50%，则黑球和白球相同，
∴若保持黑球数量不变，则白球数量：20+10=30，
若保持白球的数量不变，则黑球数为：30-10=20，
∴要使摸到黑球的可能性大小为50%，
则需要增加相同的白球10个，或减少黑球10个，
故答案为：10；10．
【点睛】本题考查了利用频率估计概率：大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．
20. 如图，已知ΔABC的三个顶点坐标为A(−3，4)、B(−7，1)、C(−2，1)．

（1）请画出关于坐标原点的中心对称图形△，并写出点的对应点的坐标： ；
（2）将绕坐标原点顺时针旋转，直接写出点的对应点的坐标： ；
（3）请直接写出：位于第三象限且与A、B、C三个顶点构成平行四边形的D的坐标： ．
【答案】（1）图见解析，（3，-4）
（2）（4，3） （3）（ -6，-2 ）
【解析】
【分析】（1）利用中心对称变换的性质分别作出A，B，C的对应点，，即可；
（2）利用旋转变换的性质分别作出A，B，C的对应点P，E，F即可；
（3）根据平行四边形的性质，画出图形可得结论．
【小问1详解】
解：如图，△即为所求，（ 3，-4 ）．
故答案为：（3，-4）；
；
【小问2详解】
解：如图，△PEF即为所求，P（4，3）．
故答案为：（4，3）；
【小问3详解】
解：如图，点D即为所求，D（-6，-2 ）．
故答案为：（-6，-2）．
【点睛】本题考查作图-旋转变换，图形与坐标，平行四边形的性质，解题的关键是掌握旋转变换的性质，属于中考常考题型．
21. 为响应全面推进中小学校“社会主义核心价值观”教育年活动．某校对全校学生进行了中期检测评价，检测结果分为A（优秀）、B（良好）、C（合格）、D（不合格）四个等级．并随机抽取若干名学生的检测结果作为样本进行数据处理，制作了如下所示不完整的统计表和统计图．
等级
频数
频率
A
a
0.3
B
35
0.35
C
31
b
D
4
0.04

请根据图表提供的信息，解答下列问题：
（1）a=　 　，b=　 　；
（2）请补全条形统计图；
（3）若该校共有学生800人，据此估算，该校学生在本次检测中达到“A（优秀）”等级的学生人数为　 　人．
【答案】（1）30，0.31；（2）详见解析；（3）240
【解析】
【分析】（1）先求出样本容量，再根据表格中的数据可以求得a、b的值；
（2）根据a的值可以将条形统计图补充完整；
（3）根据统计图中的数据可以解答本题．
【详解】解：（1）本次随机抽取样本容量为：35÷0.35=100，
a=100×0.3=30，
b=31÷100=0.31，
故答案为：30，0.31；
（2）由（2）知a=30，
补充完整的条形统计图如图所示；

（3）800×0.3=240（人），
故答案为：240．
【点睛】本题考查了条形统计图、统计表、用样本估计总体，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
22. 如图，在□ABCD中，E是BC上的一点，且AB=BE，AE、DC的延长线相交于点F，∠F=62°．求∠BAE和∠D的度数．

【答案】∠BAE=62°，∠D=56°
【解析】
【分析】由平行四边形的性质可得AB∥CD，∠B＝∠D，由平行线的性质可求∠BAE＝∠F＝62°，由等腰三角形的性质和三角形内角和定理可求∠D度数．
【详解】解：∵四边形ABCD是平行四边形，
∴AB∥CD，∠B＝∠D，
∴∠BAE＝∠F＝62°，
∵AB＝BE，
∴∠BAE＝∠BEA＝62°，
∴∠B＝180°﹣∠BAE＝∠BEA＝56°，
∴∠D＝56°．
【点睛】本题考查了平行四边形的性质，等腰三角形的性质，灵活运用平行四边形的性质是本题的关键．
23. 已知：如图，在□ABCD中，∠ABC、∠ADC的平分线分别交AD、BC于点E、F． 求证：BEDF．

【答案】见解析
【解析】
【分析】根据平行四边形的性质得出∠ABC＝∠ADC，ADBC，求出DEBF，∠EBC＝∠AEB，根据角平分线的定义求出∠ADF＝∠EBC，求出∠AEB＝∠ADF，根据平行线的判定得出BEDF即可．
【详解】证明：∵四边形ABCD是平行四边形，
∴∠ABC＝∠ADC，ADBC，
∴DEBF，∠EBC＝∠AEB，
∵∠ABC、∠ADC的平分线分别交AD、BC于点E、F，
∴∠ADF＝∠ADC，∠EBC＝∠ABC，
∴∠ADF＝∠EBC，
∴∠AEB＝∠ADF，
∴BEDF．
【点睛】本题考查了平行四边形的性质，平行线的性质，角平分线的定义等知识点，能灵活运用定理进行推理是证题的关键．
24. 如图，点C是的中点，四边形是平行四边形．
（1）求证：四边形是平行四边形；
（2）如果，求证：四边形是矩形．

【答案】（1）见解析；（2）见解析
【解析】
【分析】（1）由平行四边形的性质以及点C是BE的中点，得到AD∥CE，AD=CE，从而证明四边形ACED是平行四边形；
（2）由平行四边形的性质证得DC=AE，从而证明平行四边形ACED是矩形．
【详解】证明：（1）∵四边形ABCD是平行四边形，
∴AD∥BC，且AD=BC．
∵点C是BE的中点，
∴BC=CE，
∴AD=CE，
∵AD∥CE，
∴四边形ACED是平行四边形；
（2）∵四边形ABCD是平行四边形，
∴AB=DC，
∵AB=AE，
∴DC=AE，
∵四边形ACED是平行四边形，
∴四边形ACED是矩形．
【点睛】本题考查了平行四边形和矩形的判定和性质，正确的识别图形是解题的关键．
25. 如图，矩形ABCD中，点E在边CD上，将△BCE沿BE折叠，点C落在AD边上的点F处，过点F作FG∥CD交BE于点G，连接CG．

（1）求证：四边形CEFG是菱形；
（2）若AB=6，AD=10，求四边形CEFG的面积．
【答案】（1）见解析 （2）四边形CEFG的面积为．
【解析】
【分析】（1）根据题意和翻折的性质，可以得到△BCE≌△BFE，再根据全等三角形的性质和菱形的判定方法即可证明结论成立；
（2）根据题意和勾股定理，可以求得AF的长，进而求得EF和DF的值，从而可以得到四边形CEFG的面积．
【小问1详解】
证明：由题意可得，
△BCE≌△BFE，
∴∠BEC=∠BEF，FE=CE，
∵FG∥CE，
∴∠FGE=∠CEB，
∴∠FGE=∠FEG，
∴FG=FE，
∴FG=EC，
∴四边形CEFG平行四边形，
又∵CE=FE，
∴四边形CEFG是菱形；
【小问2详解】
解：∵矩形ABCD中，AB=6，AD=10，BC=BF，
∴∠BAF=90°，AD=BC=BF=10，
∴AF=8，
∴DF=2，
设EF=x，则CE=x，DE=6-x，
∵∠FDE=90°，
∴22+（6-x）2=x2，
解得，x=，
∴CE=，
∴四边形CEFG的面积是：CE•DF=×2=．
【点睛】本题考查翻折变化、菱形的性质和判定、矩形的性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
26. 邻边不相等的平行四边形纸片，剪去一个菱形，余下的一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；…依此类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图1，▱ABCD中，若AB＝1，BC＝2，则▱ABCD为1阶准菱形．
(1)猜想与计算：
邻边长分别为3和5平行四边形是______阶准菱形；已知▱ABCD的邻边长分别为a，b(a＞b)，满足a＝8b+r，b＝5r，请写出，▱ABCD是_____阶准菱形．
(2)操作与推理：
小明为了剪去一个菱形，进行了如下操作：如图2，把▱ABCD沿BE折叠(点E在AD上)，使点A落在BC边上的点F处，得到四边形ABFE．请证明四边形ABFE是菱形．

【答案】（1）3，12；（2）证明见解析．
【解析】
【详解】试题分析：（1）利用平行四边形准菱形的意义即可得出结论；
（2）先判断出∠AEB=∠ABE，进而判断出AE=BF，即可得出结论．
试题解析：解：（1）如图1，利用邻边长分别为3和5的平行四边形进行3次操作，所剩四边形是边长为1的菱形，故邻边长分别为3和5的平行四边形是3阶准菱形：
如图2，∵b=5r，∴a=8b+r=40r+r=8×5r+r，利用邻边长分别为41r和5r的平行四边形进行8+4=12次操作，所剩四边形是边长为1的菱形，故邻边长分别为41r和5r的平行四边形是12阶准菱形：
故答案为3，12．

（2）由折叠知：∠ABE=∠FBE，AB=BF，∵四边形ABCD是平行四边形，∴AE∥BF，∴∠AEB=∠FBE，∴∠AEB=∠ABE，∴AE=AB，∴AE=BF，∴四边形ABFE是平行四边形，∴四边形ABFE是菱形．
27. 如图，在正方形ABCD中，点E、F分别在边BC、CD上，且∠EAF ＝45°，分别连接EF、BD，BD与AF、AE分别相交于点M、N．

（1）求证：EF=BE+DF．为了证明“EF=BE+DF”，小明延长CB至点G，使BG＝DF，连接AG，请画出辅助线并按小明思路写出证明过程．
（2）若正方形ABCD的边长为6，BE=2，求DF的长．
（3）请直接写出线段BN、MN、DM三者之间的数量关系．
【答案】（1）见解析 （2）3
（3）
【解析】
【分析】（1）延长CB到G，使BG=DF，连接AG，证得△ABG≌△ADF，△AEF≌△AEG，最后利用等量代换求得答案即可；
（2）根据（1）中的结论，设正方形的边长为x，列方程可解答；
（3）在AG截取AH=AM，连接NH、BH，证得△ABH≌△ADM，△AMN≌△AHN，最后利用勾股定理求得答案即可．
【小问1详解】
证明：如图1，延长CB至点G，使BG=DF，连接AG，

∵四边形ABCD为正方形，
∴AB=AD，∠BAD=∠ADF=∠ABE=∠ABG=90°，
在△ABG和△ADF中，
，
∴△ABG≌△ADF（SAS），
∴∠DAF=∠BAG，AF=AG，
∴∠GAE=∠BAG+∠BAE=∠DAF+∠BAE=90°-45°=45°=∠EAF，
在△AEF和△AEG中，
，
∴△AEF≌△AEG（SAS），
∴EF=EG，
∵EG=BE+BG，
∴EF=BE+DF；
【小问2详解】
解：∵BC=6，BE=2，
∴EC=4，
由（1）得：EF=BE+DF=2+DF，
Rt△CEF中，，
，
解得：DF=3；
【小问3详解】
解：；
理由是：如图2，在AG上截取AH=AM，连接HN、BH，

在△AHB和△AMD中，
，
∴△AHB≌△AMD（SAS），
∴BH=DM，∠ABH=∠ADB=45°，
又∵∠ABD=45°，
∴∠HBN=90°，
∴，
在△AHN和△AMN中，
，
∴△AHN≌△AMN（SAS），
∴MN=HN，
∴．
【点睛】本题是四边形的综合题，考查了正方形的性质，全等三角形的判定和性质，勾股定理，正确的作出辅助线是解题的关键．
28. 已知，如图，为坐标原点，四边形为矩形，，，点是的中点，动点在线段上以每秒个单位长的速度由点向运动．设动点的运动时间为秒．

（1）当为何值时，四边形是平行四边形？
（2）在直线上是否存在一点，使得、、、四点为顶点的四边形是菱形？若存在，求的值，并求出点的坐标；若不存在，请说明理由．
（3）在线段上有一点，且，当运动几秒时，四边形的周长最小，并画图标出点的位置．
【答案】（1）2.5；（2）存在，，；，；，；（3），图见解析
【解析】
【分析】（1）先求出OA，进而求出OD=5，再由运动知BP=10-2t，进而由平行四边形的性质建立方程10-2t=5即可得出结论；
（2）分三种情况讨论，利用菱形的性质和勾股定理即可得出结论；
（3）先判断出四边形OAMP周长最小，得出AM+DM最小，即可确定出点M的位置，再用三角形的中位线得出BM，进而求出PC，即可得出结论．
【详解】解：∵四边形为矩形，，，
∴，，
∵点是的中点，
∴，
由运动知，，
∴，
∵四边形是平行四边形，
∴，
∴，
∴；
①当点在的右边时，如图，

∵四边形为菱形，
∴，
∴在中，由勾股定理得：，
∴，
∴，
∴
②当点在的左边且在线段上时，如图，

同①的方法得出 ，
∴，
③当点在的左边且在的延长线上时，如图，

同①的方法得出， ，
∴．
如图，

由知，，
∵，
∴，
∵，
∴四边形是平行四边形，
∴，
∵四边形的周长为
，
∴最小时，四边形的周长最小，
∴作点关于的对称点，连接交于，
∴，
∵，
∴，
∴，
∴．
【点睛】此题主要考查了矩形的性质，平行四边形的性质，极值的确定，三角形中位线定理，解（1）的关键是求出OD的值，解（2）的关键时分类讨论的思想，解（3）的关键是找出点M的位置，是一道中等难度的中考常考题．