高中数学北师大版 (2019)选择性必修 第一册3.1 独立性检验练习题

这是一份高中数学北师大版 (2019)选择性必修 第一册3.1 独立性检验练习题，共6页。试卷主要包含了下列说法正确的有，306>6，067>3，012+0，86,等内容，欢迎下载使用。

A.期望与方差B.排列与组合
C.概率D.独立性检验
答案:D
2.(多选题)下列说法正确的有( ).
A.线性回归方程对应的直线Y=b∧X+a∧至少经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点
B.命题“∀x≥1,x2+3≥4”的否定是“∃x≥1,x2+3<4”
C.样本相关系数r越小,表明两个变量之间的线性相关性越弱
D.由一个2×2列联表,得χ2≈13.079,则有99%的把握认为这两个变量间有关系
解析:线性回归方程对应的直线Y=b∧X+a∧一定经过点(x,y),可能不经过样本数据点,故A不正确;
命题“∀x≥1,x2+3≥4”的否定是“∃x≥1,x2+3<4”,故B正确;
|r|越小,表明两个变量之间的线性相关性越弱,故C不正确;
列联表中计算χ2≈13.079>6.635,故D正确.故选BD.
答案:BD
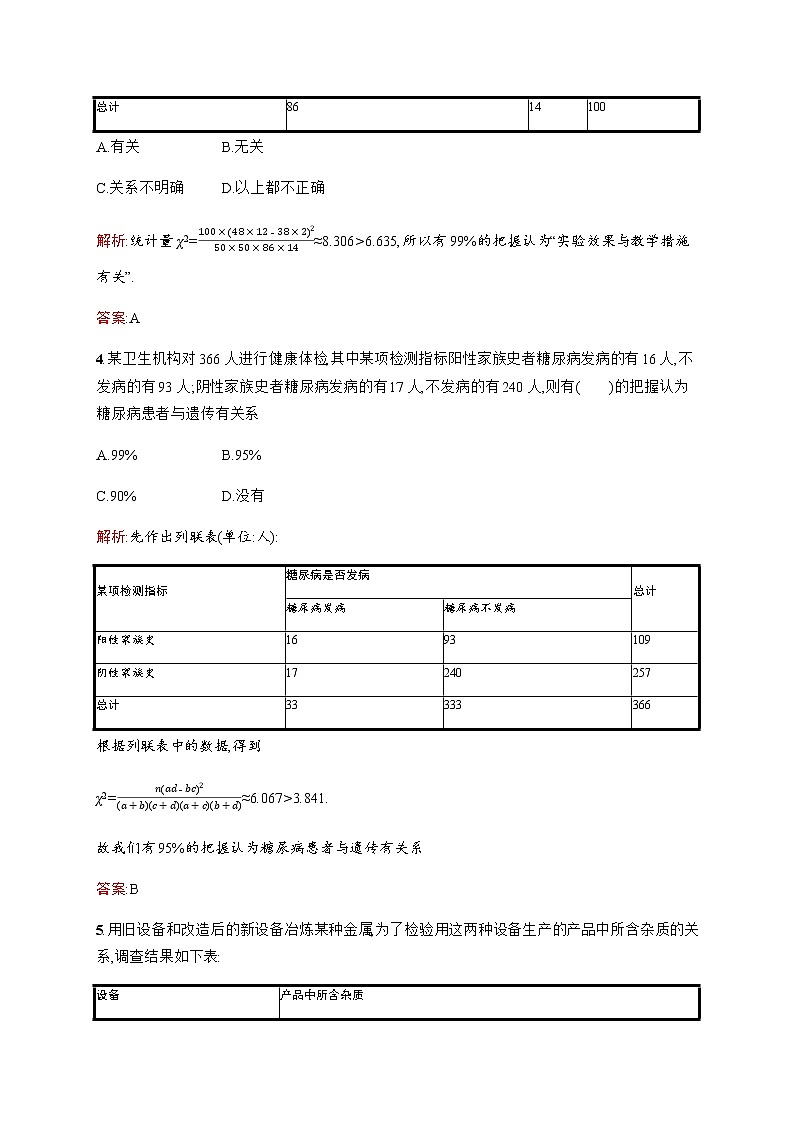
3.在两个学习基础相当的班级实行某种教学措施的实验,测试结果如表(单位:人),则有99%的把握判断实验效果与教学措施( ).
A.有关B.无关
C.关系不明确D.以上都不正确
解析:统计量χ2=100×(48×12-38×2)250×50×86×14≈8.306>6.635,所以有99%的把握认为“实验效果与教学措施有关”.
答案:A
4.某卫生机构对366人进行健康体检,其中某项检测指标阳性家族史者糖尿病发病的有16人,不发病的有93人;阴性家族史者糖尿病发病的有17人,不发病的有240人,则有( )的把握认为糖尿病患者与遗传有关系.
A.99%B.95%
C.90%D.没有
解析:先作出列联表(单位:人):
根据列联表中的数据,得到
χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)≈6.067>3.841.
故我们有95%的把握认为糖尿病患者与遗传有关系.
答案:B
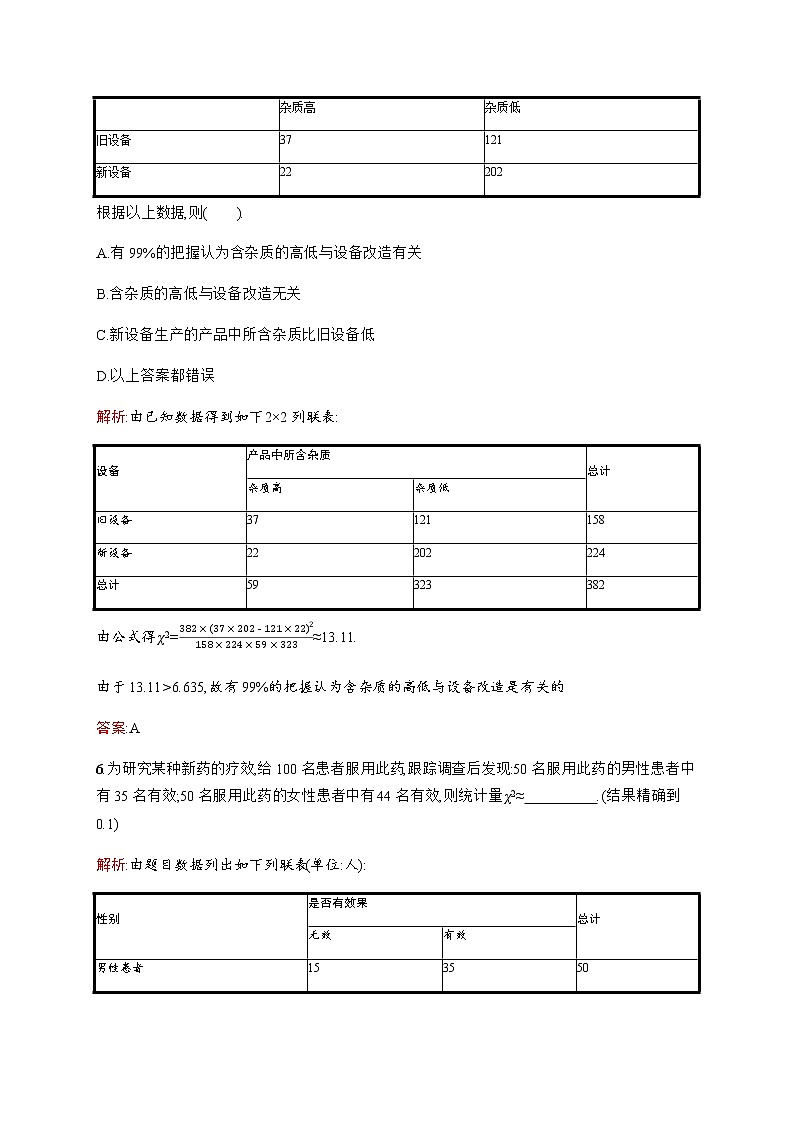
5.用旧设备和改造后的新设备冶炼某种金属,为了检验用这两种设备生产的产品中所含杂质的关系,调查结果如下表:
根据以上数据,则( ).
A.有99%的把握认为含杂质的高低与设备改造有关
B.含杂质的高低与设备改造无关
C.新设备生产的产品中所含杂质比旧设备低
D.以上答案都错误
解析:由已知数据得到如下2×2列联表:
由公式得χ2=382×(37×202-121×22)2158×224×59×323≈13.11.
由于13.11>6.635,故有99%的把握认为含杂质的高低与设备改造是有关的.
答案:A
6.为研究某种新药的疗效,给100名患者服用此药,跟踪调查后发现:50名服用此药的男性患者中有35名有效;50名服用此药的女性患者中有44名有效,则统计量χ2≈ .(结果精确到0.1)
解析:由题目数据列出如下列联表(单位:人):
由公式计算得χ2≈4.882.
答案:4.9
7.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在区间[29.94,30.06)内的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
乙厂:
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填写下面的2×2列联表,并判断两个分厂生产的零件的质量是否有差异.
解:(1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为360500=72%;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为320500=64%.
(2)2×2列联表如下:
χ2=1000×(360×180-320×140)2500×500×680×320≈7.353>6.635,所以有99%的把握认为两个分厂生产的零件的质量有差异.
8.海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:
旧养殖法
新养殖法
(第8题)
(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关;
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
参考公式:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d),其中n=a+b+c+d.
解:(1)旧养殖法的箱产量低于50kg的频率为(0.012+0.014+0.024+0.034+0.040)×5=0.62.
因此,事件A的概率估计值为0.62.
(2)根据箱产量的频率分布直方图得列联表如下(单位:网箱):
χ2=200×(62×66-34×38)2100×100×96×104≈15.705.
由于15.705>6.635,故有99%的把握认为箱产量与养殖方法有关.
(3)箱产量的频率分布直方图表明:新养殖法的箱产量平均值(或中位数)在50kg到55kg之间,旧养殖法的箱产量平均值(或中位数)在45kg到50kg之间,且新养殖法的箱产量分布集中程度较旧养殖法的箱产量分布集中程度高,因此,可以认为新养殖法的箱产量较高且稳定,从而新养殖法优于旧养殖法.
教学措施
测试结果
总计
优、良、中
差
实验班
48
2
50
对比班
38
12
50
总计
86
14
100
某项检测指标
糖尿病是否发病
总计
糖尿病发病
糖尿病不发病
阳性家族史
16
93
109
阴性家族史
17
240
257
总计
33
333
366
设备
产品中所含杂质
杂质高
杂质低
旧设备
37
121
新设备
22
202
设备
产品中所含杂质
总计
杂质高
杂质低
旧设备
37
121
158
新设备
22
202
224
总计
59
323
382
性别
是否有效果
总计
无效
有效
男性患者
15
35
50
女性患者
6
44
50
总计
21
79
100
分
组
[29.86,
29.90)
[29.90,
29.94)
[29.94,
29.98)
[29.98,
30.02)
[30.02,
30.06)
[30.06,
30.10)
[30.10,
30.14]
频
数
12
63
86
182
92
61
4
分
组
[29.86,
29.90)
[29.90,
29.94)
[29.94,
29.98)
[29.98,
30.02)
[30.02,
30.06)
[30.06,
30.10)
[30.10,
30.14]
频
数
29
71
85
159
76
62
18
是否为优质品
分厂
总计
甲厂
乙厂
优质品
非优质品
总计
是否为优质品
分厂
总计
甲厂
乙厂
优质品
360
320
680
非优质品
140
180
320
总计
500
500
1000
养殖法
箱产量
<50 kg
≥50 kg
旧养殖法
新养殖法
养殖法
箱产量
<50kg
≥50kg
旧养殖法
62
38
新养殖法
34
66