2023年河北省中考数学复习全方位第15讲 二次函数的应用 课件

这是一份2023年河北省中考数学复习全方位第15讲 二次函数的应用 课件，共60页。PPT课件主要包含了真题演练，考点梳理，题型突破等内容，欢迎下载使用。

命题点 3 二次函数与反比例函数的综合
命题点 4 二次函数与几何图形结合
1. (2014·河北,9)某种正方形合金板材的成本y(元)与它的面积成正比,设边长为x cm,当x=3时,y=18,那么当成本为72元时,边长为(　 　)A. 6 cm B. 12 cm C. 24 cm D. 36 cm
2. (2011·河北,8)一个小球被抛出后,距离地面的高度h(m)和飞行时间t(s)满足下面函数关系式:h=-5(t-1)2+6,则小球距离地面的最大高度是(　 　)A. 1 m B. 5 m C. 6 m D. 7 m
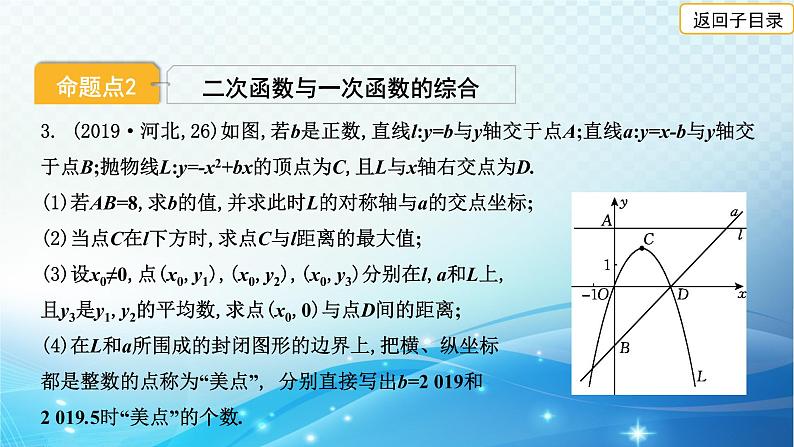
3. (2019·河北,26)如图,若b是正数,直线l:y=b与y轴交于点A;直线a:y=x-b与y轴交于点B;抛物线L:y=-x2+bx的顶点为C,且L与x轴右交点为D.(1)若AB=8,求b的值,并求此时L的对称轴与a的交点坐标;(2)当点C在l下方时,求点C与l距离的最大值;(3)设x0≠0,点(x0,y1),(x0,y2),(x0,y3)分别在l,a和L上,且y3是y1,y2的平均数,求点(x0,0)与点D间的距离;(4)在L和a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”, 分别直接写出b=2 019和2 019.5时“美点”的个数.
解:(1)当x=0时,y=x-b=-b,∴B(0,-b).∵AB=8,而A为(0,b),∴b-(-b)=8.∴b=4.∴L为y=-x2+4x.∴L的对称轴为x=2.当x=2时,y=x-4=-2.∴L的对称轴与a的交点为(2,-2).
(4)4 040;1 010.
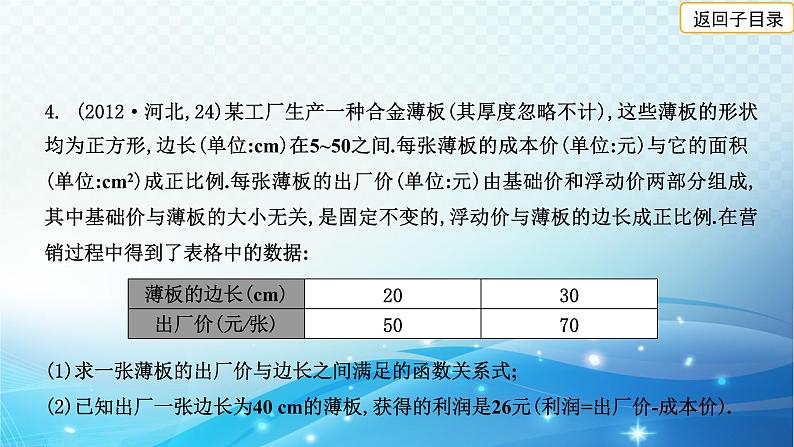
4. (2012·河北,24)某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长(单位:cm)在5~50之间.每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例.每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长成正比例.在营销过程中得到了表格中的数据:
(1)求一张薄板的出厂价与边长之间满足的函数关系式;(2)已知出厂一张边长为40 cm的薄板,获得的利润是26元(利润=出厂价-成本价).
解:(1)140,57 500.
(4)当x=5 000时,w内=337 500,w外=-5 000a+500 000,若w内w外,则a>32.5.∴当10≤a<32.5时,选择在国外销售月利润较大;当a=32.5时,在国外和国内销售月利润一样;当32.56. (2013·河北,25)某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩,Q=W+100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
(1)用含x和n的式子表示Q;(2)当x=70,Q=450时,求n的值;
(3)若n=3,要使Q最大,确定x的值;
(4)设n=2,x=40,能否在n增加m%(m>0),同时x减少m%的情况下,而Q的值仍为420,若能,求出m的值;若不能,请说明理由.
(1)求k,并用t表示h.
(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及当y=13时运动员与正下方滑道的竖直距离.(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
(3)t=1.8,v乙>7.5.提示:由题意得运动员甲的横坐标为1+5t,纵坐标为18-5t2,令18-5t2=1.8,解得t=1.8(负值已舍去),此时1+5t=10,由题意,得1+1.8v乙>10+4.5,解得v乙>7.5.
8. (2017·河北,26)某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比.经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12)符合关系式x=2n2-2kn+9(k+3)(k为常数),且得到了表中的数据.
(1)求y与x满足的关系式,请说明一件产品的利润能否是12万元;(2)求k,并推断是否存在某个月既无盈利也不亏损;(3)在这一年12个月中,若第m个月和第(m+1)个月的利润相差最大,求m.
10. (2011·河北,26)如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以每秒1个单位长的速度运动t(t>0)秒,抛物线y=x2+bx+c经过点O和点P.已知矩形ABCD的三个顶点为A(1,0),B(1,-5),D(4,0).(1)求c,b(用含t的代数式表示);(2)当4(3)在矩形ABCD的内部(不含边界),把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分,请直接写出t的取值范围.
解:(1)把x=0,y=0代入y=x2+bx+c,得c=0.再把x=t,y=0代入y=x2+bx,得t2+bt=0.∵t>0,∴b=-t.
考点 二次函数的应用
1. 应用二次函数解决实际问题的方法（1）设：设定题目中的两个变量，一般是设x是自变量，y是x的函数.（2）列：根据题目中的等量关系，列出函数解析式.（3）定：根据数学意义和实际意义确定自变量的取值范围.（4）解：利用相关性质解决问题.（5）答：检验后写出合适的答案.
2. 有关二次函数问题的常见题型（1）抛物线型解决此类问题的关键是选择合理的位置建立平面直角坐标系.建立平面直角坐标系的原则：①所建立的平面直角坐标系要使求出的二次函数解析式比较简单.②使已知点所在的位置适当（如再x轴、y轴、原点、抛物线上等），方便求二次函数的解析式和之后的求解计算.
（2）结合几何图形型解决此类问题一般是根据几何图形的性质，找自变量与该图形周长或面积之间的关系，用自变量表示出其他边的长，从而确定二次函数的解析式，再根据题意和二次函数的性质解题即可.（3）最值型①列出二次函数的解析式，并根据自变量的实际意义，确定自变量的取值范围.②配方或利用公式求顶点坐标.③检查顶点的横坐标是否在自变量的取值范围内.若在，则函数在顶点处取得最大值或最小值；若不在，则在自变量的取值范围的两端点处，根据函数增减性确定最值.
A. 7秒 B. 8秒 C. 9秒 D. 10秒
2. (2021·秦皇岛模拟)有一座抛物线形拱桥,正常水位桥下面宽度为20米,拱顶距离水平面4米,如图建立直角坐标系,若正常水位时,桥下水深6米,为保证过往船只顺利航行,桥下水面宽度不得小于18米,则当水深超过多少米时,就会影响过往船只的顺利航利(　 　)
A. 2.76米 B. 6.76米 C. 6米 D. 7米
3. (2021·河北模拟)如图,跳台滑雪是冬奥会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为(　 　)
A. 10 m B. 20 mC. 15 m D. 22.5 m
4.(2021·河北预测)如图,一座拱桥的轮廓是抛物线型,拱高OC为6m,跨度AB为20m.
(1)按如图所示的直角坐标系,求出抛物线的函数表达式;(2)拱桥内设双向行车道(正中间是一条宽为2m的隔离带),其中的一条行车道能否并排行驶宽2m,高3m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
5. (2021·唐山模拟)如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=-5x2+20x,请根据要求解答下列问题:(1)在飞行过程中,当小球的飞行高度为15 m时,飞行的时间是多少?(2)在飞行过程中,小球从飞出到落地所用时间是多少?(3)在飞行过程中,小球飞行高度何时最大?最大高度是多少?
解:(1)当y=15时有-5x2+20x=15,化简得x2-4x+3=0因式分解得(x-1)(x-3)=0,故x=1或3,即飞行时间是1秒或者3秒.
(2)飞出和落地的瞬间,高度都为0,故y=0.所以有0=-5x2+20x,解得x=0或4,所以从飞出到落地所用时间是4-0=4秒.
6. (2021·河北预测)为了给草坪喷水,安装了自动旋转喷水器,如图所示.设直线AD所在位置为地平面,喷水管AB高出地平面1.5m,在B处有一个自动旋转的喷水头,一瞬间喷出的水流呈抛物线状.喷头B与水流最高点C的连线与地平面成45°的角,水流的最高点C离地平面3.5m,水流的落地点为D.在建立如图所示的直角坐标系中:(1)求抛物线的函数解析式;(2)求水流的落地点D到点A的距离.
1. (2021·邯郸模拟)如图,假设篱笆(虚线部分)的长度是16m,则所围成的矩形ABCD的最大面积是( 　　)
A. 60m2 B. 63m2 C. 64m2 D. 66m2
2. (2021·唐山模拟)如图,在△ABC中,∠ACB=90°,∠A=30°,AB=16.设P是斜边AB上一点.过点P作PQ⊥AB,垂足为点P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为图中的( 　　)
3. (2021·原创题)某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室总占地面积最大为　　　　m2. 
4. (2021·张家口模拟)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用 32m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.(1)若花园的面积为252 m2,求x的值;(2)若在P处有一棵树与墙CD,AD的距离分别是17m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
解:(1)依题意可知BC=(32-x) m,则x(32-x)=252,解这个方程得x1=18,x2=14,答:x的值为18或14.
(2)设花园的面积为S,则S=x(32-x)=-(x-16)2+256.∵在P处有一棵树与墙CD,AD的距离是17 m和6 m,∴6≤x≤15.∴当x=15时,S最大=-(15-16)2+256=255(平方米).答:花园面积的最大值是255平方米.
5. (2021·保定模拟)某学校拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;(2)若矩形空地的面积为160 m2,求x的值;
(3)若用8 600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
(2)∵矩形空地的面积为160 m2,即y=160,∴-2x2+36x=160,x2-18x+80=0,x2-18x+81=1,(x-9)2=1.∴x1=10,x2=8.∵9≤x<18,∴x2=8(舍去).答:x的值为10.
1. (2021·秦皇岛模拟)将进货单价为70元的某种商品按零售价100元/个售出时,每天能卖出20个,若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1个,为了获得最大利润,则应降价(　 　)A. 5元　　 　B. 10元　 　　C. 15元　　 　D. 20元
2. (2021·河北预测)某商品进货单价为30元,按40元一个销售能卖40个;若销售单价每涨1元,则销量减少1个.为了获得最大利润,此商品的最佳售价应为　　　　元. 
3. (2021·石家庄模拟)商场销售服装,平均每天可售出20件,每件盈利40元,为扩大销售量,减少库存,该商场决定采取适当的降价措施,经调查发现,一件衣服降价1元,每天可多售出2件.(1)设每件降价x元,每天盈利y元,请写出y与x之间的函数关系式;(2)若商场每天要盈利1 200元,同时尽量减少库存,每件应降价多少元?(3)每件降价多少元时,商场每天盈利达到最大?最大盈利是多少元?
解:(1)y=(40-x)(20+2x)=-2x2+60x+800,∴y与x之间的函数关系式为y=-2x2+60x+800.
(2)令y=1 200,∴-2x2+60x+800=1 200,整理得x2-30x+200=0,解得x1=10(舍去),x2=20,∴商场每天要盈利1 200元,为尽量减少库存每件衬衫降价20元.
(3)y=-2x2+60x+800=-2(x-15)2+1 250,∵a=-2<0,∴当x=15时,y有最大值,其最大值为1 250.∴每件降价15元时,商场每天的盈利达到最大,最大盈利是1 250元.
4. (2021·河北模拟)某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系关于销售单价、日销售量、日销售利润的几组对应值如表:
[注:日销售利润=日销售量×(销售单价-成本单价)](1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:该产品的成本单价是　　　　元,当销售单价x=　　　元时,日销售利润w最大,最大值是　　　元; (3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3 750元的销售目标,该产品的成本单价应不超过多少元? 
(2)设成本为a元/个,则由表格可知当x=85时,w=875.∴875=175×(85-a).解得a=80.∴w=(-5x+600)(x-80)=-5x2+1 000x-48 000=-5(x-100)2+2 000,∴当x=100时,w取得最大值,此时w最大=2 000.故答案为80,100,2 000.
(3)设产品的成本单价为a元.根据题意,得(-5×90+600)(90-a)≥3 750.解得a≤65.答:该产品的成本单价应不超过65元.
5. (2021·保定模拟)绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如图,线段EF、折线ABCD分别表示该有机产品每千克的销售价y1(元)、生产成本y2(元)与产量x(kg)之间的函数关系.(1)求该产品销售价y1(元)与产量x(kg)之间的函数关系式;(2)直接写出生产成本y2(元)与产量x(kg)之间的函数关系式;(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?