

2022-2023学年河北省沧州市中考数学专项提升仿真模拟试题(3月4月)含解析
展开2022-2023学年河北省沧州市中考数学专项提升仿真模拟试题
(3月)
一.选一选(共15小题,满分45分,每小题3分)
1. 下列各组数中互为相反数的是( )
A. 5和 B. 和
C. -和 D. ﹣5和
2. 地球的表面积约为510000000km2,将510000000用科学记数法表示为( )
A. 0.51×109 B. 5.1×108 C. 5.1×109 D. 51×107
3. 下列计算正确的是( )
A a2•a3=a5 B. (a3)2=a5 C. (3a)2=6a2 D.
4. 下列图形中,既是对称图形又是轴对称图形的是( )
A B. C. D.
5. 方程的解是( )
A. x﹣9 B. x=3 C. x=9 D. x=﹣6
6. 某班同学毕业时,都将自己的照片向全班其他同学各送一张表示留念,全班共送1892张照片,如果全班有x名同学,根据题意,列出方程为( )
A. x(x+1)=1892 B. x(x−1)=1892×2
C x(x−1)=1892 D. 2x(x+1)=1892
7. 有若干个完全相同的小正方体堆成一个如图所示几何体,若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图没有变,至多可以再添加小正方体的个数为( )
A. 2 B. 3 C. 4 D. 5
8. 已知实数a,b满足条件:a2+4b2﹣a+4b+ =0,那么﹣ab的平方根是( )
A. ±2 B. 2 C. D.
9. 下列命题是真命题的是( )
A. 如果a+b=0,那么a=b=0 B. 平方根是±4
C. 有公共顶点的两个角是对顶角 D. 等腰三角形两底角相等
10. 根据下表中的信息解决问题:
数据
12
13
14
15
16
频数
6
4
5
a
1
若该组数据中位数没有大于13,则符合条件的正整数a的取值共有( )
A. 6个 B. 5个 C. 4个 D. 3个
11. 下列计算正确的是( )
A. =±3 B. 32=6 C. (﹣1)2015=﹣1 D. |﹣2|=﹣2
12. 已知:菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E, AD=6cm,则OE的长为( )
A. 6cm B. 4cm C. 3cm D. 2cm
13. 函数y=中自变量x的取值范围是( )
A. x>1 B. x≥1 C. x≤1 D. x≠1
14. 已知关于的一元二次方程的一个根为,则另一个根为( ).
A. B. C. D.
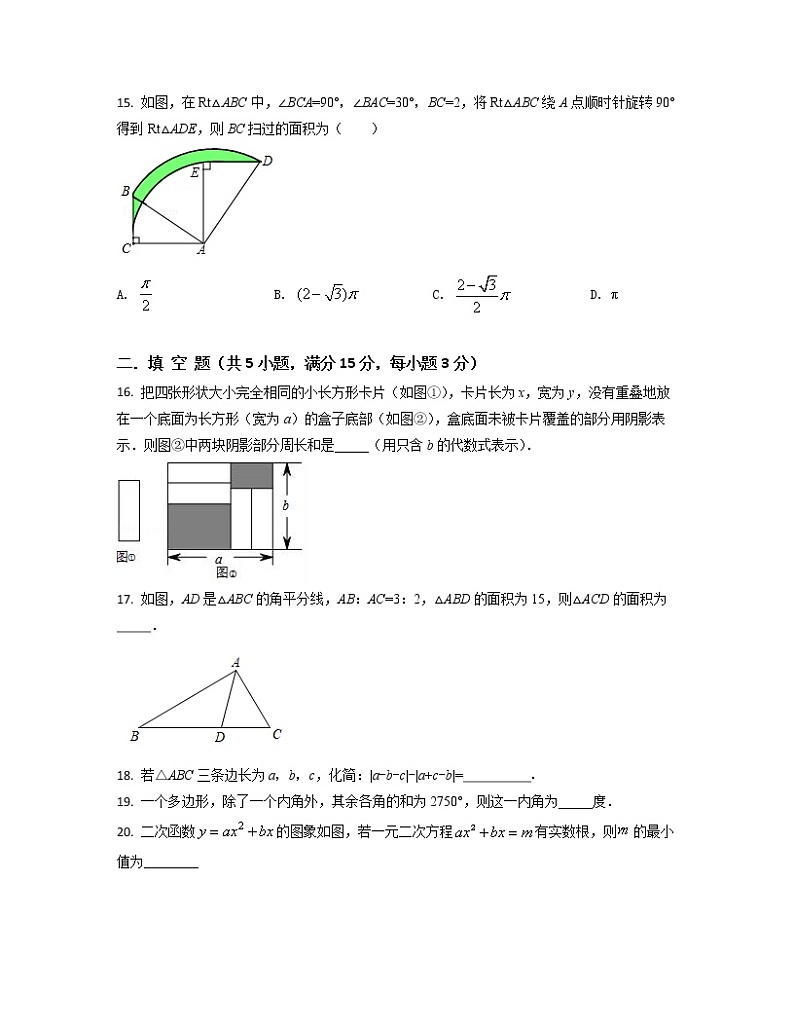
15. 如图,在Rt△ABC中,∠BCA=90°,∠BAC=30°,BC=2,将Rt△ABC绕A点顺时针旋转90°得到Rt△ADE,则BC扫过的面积为( )
A. B. C. D. π
二.填 空 题(共5小题,满分15分,每小题3分)
16. 把四张形状大小完全相同的小长方形卡片(如图①),卡片长为x,宽为y,没有重叠地放在一个底面为长方形(宽为a)的盒子底部(如图②),盒底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分周长和是_____(用只含b的代数式表示).
17. 如图,AD是△ABC的角平分线,AB:AC=3:2,△ABD的面积为15,则△ACD的面积为_____.
18. 若△ABC三条边长为a,b,c,化简:|a-b-c|-|a+c-b|=__________.
19. 一个多边形,除了一个内角外,其余各角的和为2750°,则这一内角为_____度.
20. 二次函数的图象如图,若一元二次方程有实数根,则的最小值为________
三.解 答 题(共6小题,满分60分)
21. 垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号
1
2
3
4
5
6
7
8
9
10
成绩(分)
7
6
8
7
7
5
8
7
8
7
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩且较为稳定的接球能手作为人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
22. 如图,已知点A(1,a)是反比例函数y1=的图象上一点,直线y2=﹣与反比例函数y1=的图象的交点为点B、D,且B(3,﹣1),求:
(Ⅰ)求反比例函数的解析式;
(Ⅱ)求点D坐标,并直接写出y1>y2时x的取值范围;
(Ⅲ)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到时,求点P的坐标.
23. 如图,正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C没有重合),QP与BC交于E,QP延长线与AD交于点F,连接CQ.
(1)①求证:AP=CQ;②求证:PA2=AF•AD;
(2)若AP:PC=1:3,求tan∠CBQ.
24. 某商场准备进一批两种没有同型号的衣服,已知一件A种型号比一件B种型号便宜10元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知一件A型号衣服可获利20元,一件B型号衣服可获利30元,要使在这次中获利没有少于780元,且A型号衣服没有多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种并简述购货.
25. 如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
(1)∠ACB= °,理由是: ;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.
26. 抛物线y=ax2+bx+3(a≠0)点A(﹣1,0),B(,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.
2022-2023学年河北省沧州市中考数学专项提升仿真模拟试题
(3月)
一.选一选(共15小题,满分45分,每小题3分)
1. 下列各组数中互为相反数的是( )
A. 5和 B. 和
C. -和 D. ﹣5和
【正确答案】B
【详解】A、∵,∴5和两数相等,故此选项错误;
B、∵﹣|﹣|=﹣,﹣(﹣)=,∴和是互为相反数,故此选项正确;
C、∵﹣=﹣2和=﹣2,∴和两数相等,故此选项错误;
D、∵﹣5和,没有是互为相反数,故此选项错误.
故选B.
2. 地球的表面积约为510000000km2,将510000000用科学记数法表示为( )
A. 0.51×109 B. 5.1×108 C. 5.1×109 D. 51×107
【正确答案】B
【详解】解:510 000 000=5.1×108.
故选B.
3. 下列计算正确的是( )
A. a2•a3=a5 B. (a3)2=a5 C. (3a)2=6a2 D.
【正确答案】A
【详解】A、∵a2•a3=a5,故原题计算正确;
B、∵(a3)2=a6,故原题计算错误;
C、∵(3a)2=9a2,故原题计算错误;
D、∵a2÷a8= a-6=故原题计算错误;
故选A.
4. 下列图形中,既是对称图形又是轴对称图形的是( )
A. B. C. D.
【正确答案】D
【分析】根据轴对称图形与对称图形的概念求解.
【详解】A、没有是对称图形,也没有是轴对称图形,故本选项错误;
B、没有对称图形,也没有是轴对称图形,故本选项错误;
C、没有是对称图形,也没有是轴对称图形,故本选项错误;
D、既是对称图形又是轴对称图形,故本选项正确.
故选D.
本题考查了对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,对称图形是要寻找对称,旋转180度后两部分重合.
5. 方程的解是( )
A. x﹣9 B. x=3 C. x=9 D. x=﹣6
【正确答案】C
【详解】分式方程去分母得:2x=3x﹣9,
解得:x=9,
经检验,x=9是分式方程解,
故选C.
6. 某班同学毕业时,都将自己的照片向全班其他同学各送一张表示留念,全班共送1892张照片,如果全班有x名同学,根据题意,列出方程为( )
A. x(x+1)=1892 B. x(x−1)=1892×2
C. x(x−1)=1892 D. 2x(x+1)=1892
【正确答案】C
【详解】∵全班有x名同学,
∴每名同学要送出(x-1)张;
又∵互送照片,
∴总共送的张数应该是x(x-1)=1892.
故选:C.
7. 有若干个完全相同的小正方体堆成一个如图所示几何体,若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图没有变,至多可以再添加小正方体的个数为( )
A. 2 B. 3 C. 4 D. 5
【正确答案】C
【详解】若要保持俯视图和左视图没有变,可以往第2排右侧正方体上添加1个,往第3排中间正方体上添加2个、右侧两个正方体上再添加1个,
即一共添加4个小正方体,
故选C.
8. 已知实数a,b满足条件:a2+4b2﹣a+4b+ =0,那么﹣ab的平方根是( )
A. ±2 B. 2 C. D.
【正确答案】C
【详解】整理得:(a2﹣a+)+(4b2+4b+1)=0,
(a﹣0.5)2+(2b+1)2=0,
∴a=0.5,b=﹣0.5,
∴﹣ab=0.25,
∴﹣ab的平方根是,
故选C.
9. 下列命题是真命题的是( )
A. 如果a+b=0,那么a=b=0 B. 的平方根是±4
C. 有公共顶点的两个角是对顶角 D. 等腰三角形两底角相等
【正确答案】D
【详解】解:A、如果a+b=0,那么a=b=0,或a=﹣b,错误,为假命题;
B、=4的平方根是±2,错误,为假命题;
C、有公共顶点且相等的两个角是对顶角,错误,为假命题;
D、等腰三角形两底角相等,正确,为真命题;
故选D.
10. 根据下表中的信息解决问题:
数据
12
13
14
15
16
频数
6
4
5
a
1
若该组数据的中位数没有大于13,则符合条件的正整数a的取值共有( )
A. 6个 B. 5个 C. 4个 D. 3个
【正确答案】D
【分析】直接利用a=1、2、3、4、5、6分别得出中位数,进而得出符合题意的答案.
【详解】当a=1时,有17个数据,最中间是:第9个数据,则中位数是13;
当a=2时,有18个数据,最中间是:第9和10个数据,则中位数是13;
当a=3时,有19个数据,最中间是:第10个数据,则中位数是13;
当a=4时,有20个数据,最中间是:第10和11个数据,则中位数是13.5;
当a=5时,有21个数据,最中间是:第11个数据,则中位数是14;
当a=6时,有22个数据,最中间是:第11和12个数据,则中位数是14;
故该组数据的中位数没有大于13,则符合条件的正整数a的取值共有:3个.
故选D.
此题主要考查了中位数以及频数分布表,正确把握中位数的定义是解题关键.
11. 下列计算正确的是( )
A. =±3 B. 32=6 C. (﹣1)2015=﹣1 D. |﹣2|=﹣2
【正确答案】C
【详解】A、=3,错误;
B、32=9,错误;
C、(﹣1)2015=﹣1,正确;
D、|﹣2|=2,错误,
故选C.
12. 已知:菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E, AD=6cm,则OE的长为( )
A. 6cm B. 4cm C. 3cm D. 2cm
【正确答案】C
【详解】∵四边形ABCD是菱形,
∴OB=OD,CD=AD=6cm,
∵OE∥DC,
∴OE是△BCD的中位线.
∴OE=CD=3cm.
故选:C.
13. 函数y=中自变量x的取值范围是( )
A. x>1 B. x≥1 C. x≤1 D. x≠1
【正确答案】C
【详解】解:由题意得:1﹣x≥0,解得:x≤1.故选C.
14. 已知关于的一元二次方程的一个根为,则另一个根为( ).
A. B. C. D.
【正确答案】A
【详解】∵关于 x的一元二次方程x2﹣kx﹣6=0的一个根为x=3,
∴32﹣3k﹣6=0,解得k=1,
∴x2﹣x﹣6=0,
∴(x-3)(x+2)=0,
∴x=3或x=﹣2,
故选A.
15. 如图,在Rt△ABC中,∠BCA=90°,∠BAC=30°,BC=2,将Rt△ABC绕A点顺时针旋转90°得到Rt△ADE,则BC扫过的面积为( )
A. B. C. D. π
【正确答案】D
【详解】解:在Rt△ABC中,∠BCA=90°,∠BAC=30°,BC=2,∴AC=,AB=4,∵将Rt△ABC绕点A逆时针旋转90°得到Rt△ADE,∴△ABC的面积等于△ADE的面积,∠CAB=∠DAE,AE=AC=,AD=AB=4,∴∠CAE=∠DAB=90°,∴阴影部分的面积S=S扇形BAD+S△ABC﹣S扇形CAE﹣S△ADE=+×2×﹣﹣×2×=π.故选D.
点睛:本题考查了三角形、扇形的面积,旋转的旋转,勾股定理等知识点的应用,解此题的关键是把求没有规则图形的面积转化成求规则图形(如三角形、扇形)的面积.
二.填 空 题(共5小题,满分15分,每小题3分)
16. 把四张形状大小完全相同的小长方形卡片(如图①),卡片长为x,宽为y,没有重叠地放在一个底面为长方形(宽为a)的盒子底部(如图②),盒底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分周长和是_____(用只含b的代数式表示).
【正确答案】4b.
【详解】试题解析:根据题意得:x+2y=a,
则图②中两块阴影部分周长和是2a+2(b-2y)+2(b-x)=2a+4b-4y-2x=2a+4b-2(x+2y)=2a+4b-2a=4b.
故答案为4b.
17. 如图,AD是△ABC的角平分线,AB:AC=3:2,△ABD的面积为15,则△ACD的面积为_____.
【正确答案】10
【详解】如图,
过点D作DE⊥AB于E,DF⊥AC于F,
∵AD是△ABC的角平分线,
∴DE=DF,
又∵AB:AC=3:2,
∴AB=AC,
∵△ABD的面积为15
∴S△ABD=AB×DE=×AC×DF=15,
∴AC×DF=10
∴S△ACD=AC×DF=10
故10.
本题考查了角平分线的性质;此题的关键是根据角平分线的性质,求得点D到AB的距离等于点D到AC的距离,即△ABD边AB上的高与△ACD边AC上的高相等.
18. 若△ABC三条边长为a,b,c,化简:|a-b-c|-|a+c-b|=__________.
【正确答案】2b-2a
【详解】根据三角形的三边关系得:a﹣b﹣c<0,c+a﹣b>0,
∴原式=﹣(a﹣b﹣c)﹣(a+c﹣b)=﹣a+b+c﹣a﹣c+b=2b﹣2a.
故答案为2b﹣2a
本题考查了值得化简和三角形三条边的关系:三角形任意两边之和大于第三边,任意两边之差小于第三边;一个正数的值等于它的本身,零的值还是零,一个负数的值等于它的相反数,据此解答即可.
19. 一个多边形,除了一个内角外,其余各角的和为2750°,则这一内角为_____度.
【正确答案】130
【详解】分析:n边形的内角和是 因而内角和一定是180度的倍数.而多边形的内角一定大于0,并且小于180度,因而内角和除去一个内角的值,这个值除以180度,所得数值比边数要小,小的值小于1.
详解:设多边形的边数为x,由题意有
解得
因而多边形的边数是18,
则这一内角为
故答案为
点睛:考查多边形的内角和公式,熟记多边形的内角和公式是解题的关键.
20. 二次函数的图象如图,若一元二次方程有实数根,则的最小值为________
【正确答案】-3
【分析】如图,画直线 由图像可得:当直线与函数的图像有交点时,则方程有实数根,从而可得到答案.
【详解】解:如图,画直线
当直线与函数的图像有交点时,
则方程有实数根,
由图像可得:当直线过的顶点时,有最小值,
此时:
故
本题考查的是二次函数与一元二次方程的关系,掌握利用图像法解一元二次方程是解题的关键.
三.解 答 题(共6小题,满分60分)
21. 垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号
1
2
3
4
5
6
7
8
9
10
成绩(分)
7
6
8
7
7
5
8
7
8
7
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩且较为稳定的接球能手作为人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
【正确答案】(1)7分(2)选乙运动员更合适(3)
【分析】(1)观察表格可知甲运动员测试成绩的众数和中位数都是7分;
(2)易知=7分,=7分,=6.3分,根据题意没有难判断;
(3)画出树状图,即可解决问题;
【详解】解:(1)甲运动员测试成绩的众数和中位数都是7分.
(2)∵=7分,=7分,=6.3分,
∴=>,>
∴选乙运动员更合适.
(3)树状图如图所示,
第三轮结束时球回到甲手中的概率是P(求回到甲手中)=.
22. 如图,已知点A(1,a)是反比例函数y1=的图象上一点,直线y2=﹣与反比例函数y1=的图象的交点为点B、D,且B(3,﹣1),求:
(Ⅰ)求反比例函数的解析式;
(Ⅱ)求点D坐标,并直接写出y1>y2时x的取值范围;
(Ⅲ)动点P(x,0)在x轴正半轴上运动,当线段PA与线段PB之差达到时,求点P的坐标.
【正确答案】(1)反比例函数的解析式为y=﹣;(2)D(﹣2,);﹣2<x<0或x>3;(3)P(4,0).
【详解】试题分析:(1)把点B(3,﹣1)带入反比例函数中,即可求得k的值;
(2)联立直线和反比例函数的解析式构成方程组,化简为一个一元二次方程,解方程即可得到点D坐标,观察图象可得相应x的取值范围;
(3)把A(1,a)是反比例函数的解析式,求得a的值,可得点A坐标,用待定系数法求得直线AB的解析式,令y=0,解得x的值,即可求得点P的坐标.
试题解析:(1)∵B(3,﹣1)在反比例函数的图象上,
∴-1=,
∴m=-3,
∴反比例函数的解析式为;
(2),
∴=,
x2-x-6=0,
(x-3)(x+2)=0,
x1=3,x2=-2,
当x=-2时,y=,
∴D(-2,);
y1>y2时x的取值范围是-2
(3)∵A(1,a)是反比例函数的图象上一点,
∴a=-3,
∴A(1,-3),
设直线AB为y=kx+b,
,
∴,
∴直线AB为y=x-4,
令y=0,则x=4,
∴P(4,0)
23. 如图,正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C没有重合),QP与BC交于E,QP延长线与AD交于点F,连接CQ.
(1)①求证:AP=CQ;②求证:PA2=AF•AD;
(2)若AP:PC=1:3,求tan∠CBQ.
【正确答案】(1)①证明见解析;②证明见解析;(2)
【分析】(1)①用SAS证明△ABP≌△CBQ;②利用①的结论和△EPC与△EBQ组成的“8”字形证明△APF∽△ABP;
(2)△ABP≌△CBQ,证∠PCQ=90°,由②可得∠CBQ=∠CPQ,又CQ=AP,根据正切的定义即可求解.
【详解】解:(1)①∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵△BPQ是等腰直角三角形,
∴BP=BQ,∠PBQ=90°,
∴∠PBC+∠CBQ=90°
∴∠ABP=∠CBQ,
∴△ABP≌△CBQ,
∴AP=CQ;
②∵四边形ABCD是正方形,
∴∠DAC=∠BAC=∠ACB=45°,
∵∠PQB=45°,∠CEP=∠QEB,
∴∠CBQ=∠CPQ,
由①得△ABP≌△CBQ,∠ABP=∠CBQ
∵∠CPQ=∠APF,
∴∠APF=∠ABP,
∴△APF∽△ABP,
(2)由①得△ABP≌△CBQ,
∴∠BCQ=∠BAC=45°,
∵∠ACB=45°,
∴∠PCQ=45°+45°=90°
∴tan∠CPQ=,
由①得AP=CQ,
又AP:PC=1:3,
∴tan∠CPQ,
由②得∠CBQ=∠CPQ,
∴tan∠CBQ=tan∠CPQ=.
24. 某商场准备进一批两种没有同型号的衣服,已知一件A种型号比一件B种型号便宜10元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知一件A型号衣服可获利20元,一件B型号衣服可获利30元,要使在这次中获利没有少于780元,且A型号衣服没有多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种并简述购货.
【正确答案】(1)A种型号的衣服每件90元,B种型号的衣服100元;(2)有三种进货:(1)B型号衣服购买10件,A型号衣服购进24件;(2)B型号衣服购买11件,A型号衣服购进26件;(3)B型号衣服购买12件,A型号衣服购进28件.
【详解】试题分析:(1)等量关系为:A种型号衣服9件×进价+B种型号衣服10件×进价=1810,A种型号衣服12件×进价+B种型号衣服8件×进价=1880;
(2)关键描述语是:获利没有少于699元,且A型号衣服没有多于28件.关系式为:18×A型件数+30×B型件数≥699,A型号衣服件数≤28.
试题解析:(1)设A种型号的衣服每件x元,B种型号的衣服y元,
则:,
解之得.
答:A种型号的衣服每件90元,B种型号的衣服100元;
(2)设B型号衣服购进m件,则A型号衣服购进(2m+4)件,
可得:,
解之得192⩽m⩽12,
∵m为正整数,
∴m=10、11、12,2m+4=24、26、28.
答:有三种进货:
(1)B型号衣服购买10件,A型号衣服购进24件;
(2)B型号衣服购买11件,A型号衣服购进26件;
(3)B型号衣服购买12件,A型号衣服购进28件.
点睛:点睛:本题主要考查二元方程组和一元没有等式组的实际问题的应用,解题的关键是读懂题目的意思,根据题目给出的条件,设出未知数,分别找出甲组和乙组对应的工作时间,找出合适的等量关系,列出方程组,再求解.
25. 如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
(1)∠ACB= °,理由是: ;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.
【正确答案】(1)90°;直径所对的圆周角是直角;(2)证明见解析;(3)
【详解】试题分析:(1)根据AB是⊙O的直径,点C在⊙O上利用直径所对的圆周角是直角即可得到结论;
(2)根据∠ABC的平分线与AC相交于点D,得到∠CBD=∠ABE,再根据AE是⊙O的切线得到∠EAB=90°,从而得到∠CDB+∠CBD=90°,等量代换得到∠AED=∠EDA,从而判定△EAD是等腰三角形.
(3)证得△CDB∽△AEB后设BD=5x,则CB=4x,CD=3x,从而得到CA=CD+DA=3x+6,然后在直角三角形ACB中,利用AC2+BC2=AB2得到(3x+6)2+(4x)2=82解得x后即可求得BD的长.
试题解析:(1)∵AB是⊙O的直径,点C在⊙O上,
∴∠ACB=90°(直径所对的圆周角是直角)
(2)△EAD是等腰三角形.
证明:∵∠ABC的平分线与AC相交于点D,
∴∠CBD=∠ABE
∵AE是⊙O的切线,∴∠EAB=90°
∴∠AEB+∠EBA=90°,
∵∠EDA=∠CDB,∠CDB+∠CBD=90°,
∵∠CBE=∠ABE,
∴∠AED=∠EDA,
∴AE=AD
∴△EAD是等腰三角形.
(3)解:∵AE=AD,AD=6,
∴AE=AD=6,
∵AB=8,
∴在直角三角形AEB中,EB=10
∵∠CDB=∠E,∠CBD=∠ABE
∴△CDB∽△AEB,
∴,
∴设CB=4x,CD=3x则BD=5x,
∴CA=CD+DA=3x+6,
在直角三角形ACB中,
AC2+BC2=AB2
即:(3x+6)2+(4x)2=82,
解得:x=﹣2(舍去)或x=
∴BD=5x=.
点睛:本题考查了圆的综合知识,题目中涉及到了圆周角定理、等腰三角形的性质与判定以及相似三角形的判定与性质,难度中等偏上.
26. 抛物线y=ax2+bx+3(a≠0)点A(﹣1,0),B(,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.
【正确答案】(1)y=﹣2x2+x+3;(2)∠ACB=45°;(3)D.
【详解】试题分析:把点的坐标代入即可求得抛物线的解析式.
作BH⊥AC于点H,求出的长度,即可求出∠ACB的度数.
延长CD交x轴于点G,△DCE∽△AOC,只可能∠=∠DCE.求出直线的方程,和抛物线的方程联立即可求得点的坐标.
试题解析:(1)由题意,得
解得.
∴这条抛物线的表达式为.
(2)作BH⊥AC于点H,
∵A点坐标是(-1,0),C点坐标是(0,3),B点坐标是(,0),
∴AC=,AB=,OC=3,BC=.
∵,即∠BAD=,
∴.
Rt△ BCH中,,BC=,∠BHC=90º,
∴.
又∵∠ACB是锐角,∴.
(3)延长CD交x轴于点G,
∵Rt△ AOC中,AO=1,AC=,
∴.
∵△DCE∽△AOC,∴只可能∠=∠DCE.
∴AG = CG.
∴.
∴AG=5.∴G点坐标是(4,0).
∵点C坐标是(0,3),∴.
∴ 解得,(舍)
∴点D坐标是
2022-2023学年河北省沧州市中考数学专项提升仿真模拟试题
(4月)
一.选一选(共10小题,满分30分,每小题3分)
1. 下列四个数中,与﹣2的和为0的数是( )
A. ﹣2 B. 2 C. 0 D. ﹣
2. 下列各数中最小的数是( )
A. B. ﹣1 C. D. 0
3. 如图,已知直线、被直线所截,,E是直线右边任意一点(点E没有在直线,上),设,.下列各式:①,②,③,④,的度数可能是( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
4. 下列运算正确的是
A. a2 +a2= a4 B. 2a2·3a3= 6a6 C. 8 a = 23 +a D. (-3a)2=9a2
5. 下列中,最适合采用普查方式的是( )
A. 对太原市民知晓“中国梦”内涵情况
B. 对全班同学1分钟仰卧起坐成绩的
C. 对2018年央视春节联欢晚会收视率的
D. 对2017年全国快递包裹产生的包装数量的
6. 一个几何体由大小相同的小正方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在这个位置小正方体的个数.从左面看到的这个几何体的形状图的是( )
A. B. C. D.
7. 从一副扑克牌中抽出如下四张牌,其中是对称图形的有( )
A. 1张 B. 2张 C. 3张 D. 4张
8. 二次函数y=ax2+bx+c(a≠0)部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(-2,y1),点B(,y2),点C(,y3)在该函数图象上,则y1<y3<y2;其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 1个
9. AD与BE是△ABC的角平分线,D,E分别在BC,AC上,若AD=AB,BE=BC,则∠C=( )
A. 69° B. C. D. 没有能确定
10. 直角三角形的三边为a﹣b,a,a+b且a、b都为正整数,则三角形其中一边长可能为( )
A. 61 B. 71 C. 81 D. 91
二.填 空 题(共6小题,满分18分,每小题3分)
11. 2015年重庆力帆足球队再次征战中国足球超级联赛,重庆球迷热情高涨,球市异常火爆,第二轮比赛主场对阵卫冕广州恒大队,重庆奥体涌现48500多名球迷支持家乡球队,将48500用科学记数法表示为_____.
12. 如图,AD是△ABC的角平分线,AB:AC=3:2,△ABD的面积为15,则△ACD的面积为_____.
13. 若没有等式组无解,则m的取值范围是______.
14. 有一个正六面体,六个面上分别写有1~6这6个整数,投掷这个正六面体,向上一面的数字是2的倍数或3的倍数的概率是____.
15. ⊙O的直径为10,弦AB=8,点P为AB上一动点,若OP的值为整数,则满足条件的P点有_____个.
16. △ABC中,BC=10,AB=,∠ABC=30°,点P在直线AC上,点P到直线AB的距离为1,则CP的长为_____.
三.解 答 题(共9小题,满分72分)
17. 先化简,再求值:,其中x满足x2+7x=0.
18. 如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.
求证:(1)∠CEB=∠CBE;
(2)四边形BCED是菱形.
19. 典典同学学完统计知识后,随机了她家所在辖区若干名居民的年龄,将数据绘制成如下扇形和条形统计图:
请根据以上没有完整统计图提供的信息,解答下列问题:
(1)扇形统计图中a= ,b= ;并补全条形统计图;
(2)若该辖区共有居民3500人,请估计年龄在0~14岁的居民的人数.
(3),典典知道了辖区内60岁以上的部分老人参加了市级门球比赛,比赛的老人们分成甲、乙两组,典典很想知道甲乙两组的比赛结果,王大爷告诉说,甲组与乙组的得分和为110,甲组得分没有低于乙组得分的1.5倍,甲组得分至少为多少?
20. 某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
21. 如图,在平面直角坐标系xOy中,函数y=kx+b的图象与反比例函数y=的图象相交于点A(m,3)、B(–6,n),与x轴交于点C.
(1)求函数y=kx+b的关系式;
(2)图象,直接写出满足kx+b>x的取值范围;
(3)若点P在x轴上,且S△ACP=,求点P的坐标.
22. 如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
23. 一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的速度.
24. 阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE,
(1)在图1中证明小胖发现;
借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;
(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).
25. 抛物线y=ax2+bx+3(a≠0)点A(﹣1,0),B(,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.
2022-2023学年河北省沧州市中考数学专项提升仿真模拟试题
(4月)
一.选一选(共10小题,满分30分,每小题3分)
1. 下列四个数中,与﹣2和为0的数是( )
A. ﹣2 B. 2 C. 0 D. ﹣
【正确答案】B
【详解】分析:找出-2的相反数即为所求.
详解:下列四个数中,与-2的和为0的数是2,
故选B.
点睛:此题考查了相反数,熟练掌握相反数的定义是解本题的关键.
2. 下列各数中最小的数是( )
A. B. ﹣1 C. D. 0
【正确答案】C
【详解】根据实数比较大小的方法,可得
﹣<﹣<﹣1<0,
∴各数中最小的数是:﹣.
故选C.
3. 如图,已知直线、被直线所截,,E是直线右边任意一点(点E没有在直线,上),设,.下列各式:①,②,③,④,的度数可能是( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
【正确答案】A
【分析】根据点E有3种可能位置,分情况进行讨论,依据平行线的性质以及三角形外角性质进行计算求解即可.
【详解】解:(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β-α.
(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.
(3)当点E在CD的下方时,同理可得,∠AEC=α-β.
综上所述,∠AEC的度数可能为β-α,α+β,α-β.
即①α+β,②α-β,③β-α,都成立.
故选A.
本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同位角相等;两直线平行,内错角相等.
4. 下列运算正确的是
A. a2 +a2= a4 B. 2a2·3a3= 6a6 C. 8 a = 23 +a D. (-3a)2=9a2
【正确答案】D
【详解】A.a2 +a2=2a2,故本选项错误;
B.2a2·3a3= 6a5,故本选项错误;
C.8 a = (23)a = 23a,故本选项错误;
D.(-3a)2=9a2,故本选项正确.
故选D.
5. 下列中,最适合采用普查方式的是( )
A. 对太原市民知晓“中国梦”内涵情况的
B. 对全班同学1分钟仰卧起坐成绩的
C. 对2018年央视春节联欢晚会收视率的
D. 对2017年全国快递包裹产生的包装数量的
【正确答案】B
【详解】分析:由普查得到的结果比较准确,但所费人力、物力和时间较多,而抽样得到的结果比较近似.
详解:A、范围广适合抽样,故A没有符合题意;
B、适合普查,故B符合题意;
C、范围广适合抽样,故C没有符合题意;
D、范围广适合抽样,故D没有符合题意;
故选B.
点睛:本题考查了抽样和全面的区别,选择普查还是抽样要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的、无法进行普查、普查的意义或没有大,应选择抽样,对于度要求高的,事关重大的往往选用普查.
6. 一个几何体由大小相同的小正方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在这个位置小正方体的个数.从左面看到的这个几何体的形状图的是( )
A. B. C. D.
【正确答案】B
【详解】分析:由已知条件可知,从正面看有3列,每列小正方数形数目分别为4,3,2;从左面看有3列,每列小正方形数目分别为1,4,3.据此可画出图形.
详解:由俯视图及其小正方体的分布情况知,
该几何体的主视图为:
该几何体的左视图为:
故选B.
点睛:此题主要考查了几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视图的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的数字.
7. 从一副扑克牌中抽出如下四张牌,其中是对称图形的有( )
A. 1张 B. 2张 C. 3张 D. 4张
【正确答案】B
【详解】试题解析:旋转180°以后,第2张与第3张,中间的图形相对位置改变,因而没有是对称图形;
第1,4张是对称图形.故选B.
8. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(-2,y1),点B(,y2),点C(,y3)在该函数图象上,则y1<y3<y2;其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 1个
【正确答案】A
【详解】解:∵抛物线的对称轴为直线x=-=2,
∴b=-4a,∴4a+b=0,故(1)正确;
由图象知,当x=-2时,y=4a-2b+c<0,∴4a+c<2b,故(2)错误;
∵图象过点(-1,0),
∴a-b+c=0,即c=-a+b=-a-4a=-5a,
∴5a+3c=5a-15a=-10a,
∵抛物线的开口向下,
∴a<0,
∴5a+3c=-10a>0,故(3)正确;
由图象知抛物线的开口向下,对称轴为直线x=2,
∴离对称轴水平距离越远,函数值越小,
∴y1<y2<y3,故(4)错误.
综上(1)(3)正确.
故选A.
9. AD与BE是△ABC角平分线,D,E分别在BC,AC上,若AD=AB,BE=BC,则∠C=( )
A. 69° B. C. D. 没有能确定
【正确答案】C
【详解】分析:根据AD=AB和三角形内角和、外角性质,寻找∠C和∠BAC的关系的表达式;再根据BE=BC,寻找∠C和∠BAC关系的另一种表达式,由此可得关于∠BAC的方程,求得的度数,代入即可求得∠C.
详解:
∵AD=AB,
∴∠ADB=(180°﹣∠BAC)=90°﹣∠BAC,
∴∠C=∠ADB﹣∠DAC=(180°﹣∠BAC)=90°﹣∠BAC﹣∠BAC=90°﹣∠BAC;
∵BE=BC,
∴∠C=∠BEC=∠BAC+∠ABE=∠BAC+(180°﹣∠BAC)=∠BAC+45°﹣∠BAC=45°+∠BAC,
∴90°﹣∠BAC=45°+∠BAC,
解得∠BAC=,
∴∠C=90°﹣.
故选C.
点睛:综合考查角平分线的定义、外角的性质、三角形的内角和和等边对等角等知识点,解题关键是找角之间的关系.
10. 直角三角形的三边为a﹣b,a,a+b且a、b都为正整数,则三角形其中一边长可能为( )
A. 61 B. 71 C. 81 D. 91
【正确答案】C
【详解】由题可知:(a−b)2+a2=(a+b)2,解之得:a=4b,
所以直角三角形三边分别为3b、4b、5b.
当b=27时,3b=81.
故选C.
二.填 空 题(共6小题,满分18分,每小题3分)
11. 2015年重庆力帆足球队再次征战中国足球超级联赛,重庆球迷热情高涨,球市异常火爆,第二轮比赛主场对阵卫冕广州恒大队,重庆奥体涌现48500多名球迷支持家乡球队,将48500用科学记数法表示为_____.
【正确答案】4.85×105
【详解】分析:由48500的数位为5,利用科学记数法表示即可.
详解:48500=4.85×105.
故答案为4.85×105
点睛:此题考查了科学记数法-表示较大的数,将一个较大的数表示为a×10n(1≤a<10的整数,n为正整数).
12. 如图,AD是△ABC的角平分线,AB:AC=3:2,△ABD的面积为15,则△ACD的面积为_____.
【正确答案】10
【详解】如图,
过点D作DE⊥AB于E,DF⊥AC于F,
∵AD是△ABC的角平分线,
∴DE=DF,
又∵AB:AC=3:2,
∴AB=AC,
∵△ABD的面积为15
∴S△ABD=AB×DE=×AC×DF=15,
∴AC×DF=10
∴S△ACD=AC×DF=10
故10.
本题考查了角平分线的性质;此题的关键是根据角平分线的性质,求得点D到AB的距离等于点D到AC的距离,即△ABD边AB上的高与△ACD边AC上的高相等.
13. 若没有等式组无解,则m的取值范围是______.
【正确答案】
【详解】2x-3≥0,解得x≥;因无解,可得,故答案为.
点睛:本题主要考查了已知一元没有等式组的解集,求没有等式组中的字母的值,同样也是利用口诀求解.求没有等式组解集的口诀:同大取大,同小取小,大小小大中间找,小小找没有到(无解).
14. 有一个正六面体,六个面上分别写有1~6这6个整数,投掷这个正六面体,向上一面的数字是2的倍数或3的倍数的概率是____.
【正确答案】
【详解】∵投掷这个正六面体,向上的一面有6种情况,向上一面的数字是2的倍数或3的倍数的有2、3、4、6共4种情况,
∴其概率是=.
此题考查概率的求法:如果一个有n种可能,而且这些的可能性相同,其中A出现m种结果,那么A的概率P(A)=.
15. ⊙O的直径为10,弦AB=8,点P为AB上一动点,若OP的值为整数,则满足条件的P点有_____个.
【正确答案】5
【详解】分析:先求出OP的取值范围,然后再根据OP长为整数的条件来判断符合要求的P点有几个.
详解:过O作OC⊥AB于C,连接OA;
Rt△OAC中,OA=5cm,AC=4cm;
∴OC==3cm;
∴3≤OP≤5;
故OP=3cm,或4cm,或5cm;
当OP=3cm时,P与C点重合,有一个符合条件的P点;
当OP=4cm时,P位于AC或BC之间,有两个符合条件的P点;
当OP=5cm时,P与A或B重合,有两个符合条件P点;
故满足条件的P点有5个.
点睛:此题主要考查垂径定理及勾股定理的应用,能够正确的判断出OP长的大致取值,是解答此题的关键.
16. △ABC中,BC=10,AB=,∠ABC=30°,点P在直线AC上,点P到直线AB的距离为1,则CP的长为_____.
【正确答案】或 .
【详解】分析:过点C作CD⊥AB交BA的延长线于点D,根据∠ABC的正弦和余弦可以求出CD、BD的长度,从而可以求出AD的长度,然后利用勾股定理即可求出AC的长度,再利用相似三角形对应边成比例列式求出AP的长度,再分点P在线段AC上与点P在射线CA上两种情况讨论求解.
详解:如图,过点C作CD⊥AB交BA的延长线于点D,
∵BC=10,∠ABC=30°,
∴CD=BCsin30°=5,
BD=BCcos30°=5,
∵AB=4,
∴AD=BD-AB=5-4=,
在Rt△ACD中,AC==.
过P作PE⊥AB,与BA的延长线于点E,
∵点P在直线AC上,点P到直线AB的距离为1,
∴△APE∽△ACD,
∴,
即,
解得AP=,
∴①点P在线段AC上时,CP=AC-AP=2-=,
②点P在射线CA上时,CP=AC+AP=2+=.
综上所述,CP的长为或.
故答案为或.
点睛:本题考查了解直角三角形,作出图形,利用好30°的角构造出直角三角形是解题的关键,要注意分情况讨论,避免漏解.
三.解 答 题(共9小题,满分72分)
17. 先化简,再求值:,其中x满足x2+7x=0.
【正确答案】,
【分析】由x满足x2+7x=0,可得到x=0或-7;先将括号内通分,合并;再将除法问题转化为乘法问题;约分化简后,在原式有意义的条件下,代入计算即可.
【详解】原式
又
∴x(x+7)=0,
当x=0时,原式0做除数无意义;
故当x=−7时,原式
18. 如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.
求证:(1)∠CEB=∠CBE;
(2)四边形BCED是菱形.
【正确答案】证明见解析
【详解】试题分析:(1)根据已知条件易证∠CEB=∠ABD,∠CBE=∠ABD,即可得∠CEB=∠CBE;(2)易证明四边形CEDB是平行四边形,再根据BC=BD判定四边形CEDB是菱形即可.
试题解析:证明;(1)∵△ABC≌△ABD,
∴∠ABC=∠ABD,
∵CE∥BD,
∴∠CEB=∠DBE,
∴∠CEB=∠CBE.
(2))∵△ABC≌△ABD,
∴BC=BD,
∵∠CEB=∠CBE,
∴CE=CB,
∴CE=BD
∵CE∥BD,
∴四边形CEDB是平行四边形,
∵BC=BD,
∴四边形CEDB是菱形.
考点:全等三角形的性质;菱形的判定.
19. 典典同学学完统计知识后,随机了她家所在辖区若干名居民的年龄,将数据绘制成如下扇形和条形统计图:
请根据以上没有完整的统计图提供的信息,解答下列问题:
(1)扇形统计图中a= ,b= ;并补全条形统计图;
(2)若该辖区共有居民3500人,请估计年龄在0~14岁的居民的人数.
(3),典典知道了辖区内60岁以上的部分老人参加了市级门球比赛,比赛的老人们分成甲、乙两组,典典很想知道甲乙两组的比赛结果,王大爷告诉说,甲组与乙组的得分和为110,甲组得分没有低于乙组得分的1.5倍,甲组得分至少为多少?
【正确答案】(1)20%,12%;(2)700人;(3)甲组至少得66分.
【详解】试题分析:(1)根据“15~40”的百分比和频数可求总数,进而求出b和a的值.利用总数和百分比求出频数再补全条形图;
(2)用样本估计总体即可;
(3)首先设甲组得x分,则乙组得(110﹣x)分,由题意得没有等关系:甲组得x分≥乙组得x分×1.5,根据没有等关系列出没有等式,解没有等式即可.
试题解析:解:(1)总人数:230÷46%=500(人),100÷500×=20%,60÷500×=12%;
500×22%=110(人),如图所示:
(2)3500×20%=700(人);
(3)设甲组得x分,则乙组得(110﹣x)分,由题意得:
x≥1.5(110﹣x),解得:x≥66.
答:甲组至少得66分.
20. 某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
【正确答案】(1)工厂每天能配套组成48套GH型电子产品;(2) 30名.
【分析】(1)设x人加工G型装置,y人加工H型装置,利用每个工人每天能加工6个G型装置或3个H型装置得出等式求出答案;
(2)利用每天加工的G、H型装置数量正好全部配套组成GH型产品得出等式表示出x的值,进而利用没有等式解法得出答案.
【详解】解:(1)解:设x人加工G型装置,y人加工H型装置,由题意可得:
解得:,
6×32÷4=48(套),
答:按照这样的生产方式,工厂每天能配套组成48套GH型电子产品.
(2)由题意可知:3(6x+4m)=3(80-x)×4,
解得:x=,
×4=240(个),
6x+4m≥240 ,
6×+4m≥240.
解得:m≥30.
答:至少需要补充30名新工人才能在规定期内完成总任务.
21. 如图,在平面直角坐标系xOy中,函数y=kx+b的图象与反比例函数y=的图象相交于点A(m,3)、B(–6,n),与x轴交于点C.
(1)求函数y=kx+b的关系式;
(2)图象,直接写出满足kx+b>的x的取值范围;
(3)若点P在x轴上,且S△ACP=,求点P的坐标.
【正确答案】(1);(2)-6<x<0或2<x;(3)(-2,0)或(-6,0)
【分析】(1)利用反比例函数图象上点的坐标特征可求出点A、B的坐标,再利用待定系数法即可求出直线AB的解析式;
(2)根据函数图像判断即可;
(3)利用函数图象上点的坐标特征可求出点C的坐标,设点P的坐标为(x,0),根据三角形的面积公式S△ACP=S△BOC,即可得出|x+4|=2,解之即可得出结论.
【详解】(1)∵点A(m,3),B(-6,n)在双曲线y=上,
∴m=2,n=-1,
∴A(2,3),B(-6,-1).
将(2,3),B(-6,-1)带入y=kx+b,
得:,解得,.
∴直线的解析式为y=x+2.
(2)由函数图像可知,当kx+b>时,-6<x<0或2<x;
(3)当y=x+2=0时,x=-4,
∴点C(-4,0).
设点P的坐标为(x,0),如图,
∵S△ACP=S△BOC,A(2,3),B(-6,-1),
∴×3|x-(-4)|=××|0-(-4)|×|-1|,即|x+4|=2,
解得:x1=-6,x2=-2.
∴点P的坐标为(-6,0)或(-2,0).
本题考查了反比例函数与函数的交点问题、(反比例)函数图象上点的坐标特征、待定系数法求函数解析式以及三角形的面积,解题的关键是:(1)根据点的坐标利用待定系数法求出直线AB的解析式;(2)根据函数图像判断没有等式取值范围;(3)根据三角形的面积公式以及S△ACP=S△BOC,得出|x+4|=2.
22. 如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
【正确答案】(1)证明见解析;(2)
【详解】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得≌ 即可得,则可证得为的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得 利用勾股定理即可求得的长,又由OE∥AB,证得根据相似三角形的对应边成比例,即可求得的长,然后利用三角函数的知识,求得与的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,
∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
∴△COE≌△DOE(SAS),
∴ED⊥OD,
∴ED是的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
∵OE∥AB,
∴△COE∽△CAB,
∴AB=5,
∵AC是直径,
∵EF∥AB,
∴S△ADF=S梯形ABEF−S梯形DBEF
∴△ADF的面积为
23. 一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的速度.
【正确答案】(1)v=(2<t≤5) (2)8米/分
【详解】分析:(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=2代入(1)中二次函数解析式即可.
详解:(1)v=at2的图象点(1,2),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=,
由题意知,图象点(2,8),
∴k=16,
∴反比例函数的解析式为v=(2<t≤5);
(2)∵二次函数v=2t2,(0≤t≤2)的图象开口向上,对称轴为y轴,
∴弹珠在轨道上行驶的速度在2秒末,为8米/分.
点睛:本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息:自变量的取值范围和图象所的点的坐标.
24. 阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE,
(1)在图1中证明小胖的发现;
借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;
(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).
【正确答案】(1)证明见解析;(2)证明见解析;(3)∠EAF =m°.
【详解】分析:(1)如图1中,欲证明BD=EC,只要证明△DAB≌△EAC即可;
(2)如图2中,延长DC到E,使得DB=DE.首先证明△BDE等边三角形,再证明△ABD≌△CBE即可解决问题;
(3)如图3中,将AE绕点E逆时针旋转m°得到AG,连接CG、EG、EF、FG,延长ED到M,使得DM=DE,连接FM、CM.想办法证明△AFE≌△AFG,可得∠EAF=∠FAG=m°.
详(1)证明:如图1中,
∵∠BAC=∠DAE,
∴∠DAB=∠EAC,
在△DAB和△EAC中,
,
∴△DAB≌△EAC,
∴BD=EC.
(2)证明:如图2中,延长DC到E,使得DB=DE.
∵DB=DE,∠BDC=60°,
∴△BDE是等边三角形,
∴∠BD=BE,∠DBE=∠ABC=60°,
∴∠ABD=∠CBE,
∵AB=BC,
∴△ABD≌△CBE,
∴AD=EC,
∴BD=DE=DC+CE=DC+AD.
∴AD+CD=BD.
(3)如图3中,将AE绕点E逆时针旋转m°得到AG,连接CG、EG、EF、FG,延长ED到M,使得DM=DE,连接FM、CM.
由(1)可知△EAB≌△GAC,
∴∠1=∠2,BE=CG,
∵BD=DC,∠BDE=∠CDM,DE=DM,
∴△EDB≌△MDC,
∴EM=CM=CG,∠EBC=∠MCD,
∵∠EBC=∠ACF,
∴∠MCD=∠ACF,
∴∠FCM=∠ACB=∠ABC,
∴∠1=3=∠2,
∴∠FCG=∠ACB=∠MCF,
∵CF=CF,CG=CM,
∴△CFG≌△CFM,
∴FG=FM,
∵ED=DM,DF⊥EM,
∴FE=FM=FG,
∵AE=AG,AF=AF,
∴△AFE≌△AFG,
∴∠EAF=∠FAG=m°.
点睛:本题考查几何变换综合题、旋转变换、等腰三角形的性质、全等三角形的判定和性质等知识,解题的关键是学会利用“手拉手”图形中的全等三角形解决问题,学会构造“手拉手”模型,解决实际问题,属于中考压轴题.
25. 抛物线y=ax2+bx+3(a≠0)点A(﹣1,0),B(,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.
【正确答案】(1)y=﹣2x2+x+3;(2)∠ACB=45°;(3)D.
【详解】试题分析:把点的坐标代入即可求得抛物线的解析式.
作BH⊥AC于点H,求出的长度,即可求出∠ACB的度数.
延长CD交x轴于点G,△DCE∽△AOC,只可能∠=∠DCE.求出直线的方程,和抛物线的方程联立即可求得点的坐标.
试题解析:(1)由题意,得
解得.
∴这条抛物线的表达式为.
(2)作BH⊥AC于点H,
∵A点坐标是(-1,0),C点坐标是(0,3),B点坐标是(,0),
∴AC=,AB=,OC=3,BC=.
∵,即∠BAD=,
∴.
Rt△ BCH中,,BC=,∠BHC=90º,
∴.
又∵∠ACB是锐角,∴.
(3)延长CD交x轴于点G,
∵Rt△ AOC中,AO=1,AC=,
∴.
∵△DCE∽△AOC,∴只可能∠=∠DCE.
∴AG = CG.
∴.
∴AG=5.∴G点坐标(4,0).
∵点C坐标是(0,3),∴.
∴ 解得,(舍).
∴点D坐标是
2022-2023学年河北省保定市中考数学专项提升仿真模拟试题(3月4月)含解析: 这是一份2022-2023学年河北省保定市中考数学专项提升仿真模拟试题(3月4月)含解析,共61页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。
2022-2023学年河北省秦皇岛市中考数学专项提升仿真模拟试题(一模二模)含解析: 这是一份2022-2023学年河北省秦皇岛市中考数学专项提升仿真模拟试题(一模二模)含解析,共61页。试卷主要包含了解 答 题等内容,欢迎下载使用。
2022-2023学年河北省唐山市中考数学专项提升仿真模拟试题(一模二模)含解析: 这是一份2022-2023学年河北省唐山市中考数学专项提升仿真模拟试题(一模二模)含解析,共53页。试卷主要包含了填 空 题,解 答 题等内容,欢迎下载使用。












