2022-2023学年北京区域联考中考数学专项提升仿真模拟测试题(一模二模)含解析
展开2022-2023学年北京区域联考中考数学专项提升仿真模拟测试题(一模)
一、选一选:
1. 2sin60°的值等于( )
A. 1 B. C. D.
2. 方程(m–2)x2+3mx+1=0是关于x的一元二次方程,则( )
A. m≠±2 B. m=2 C. m=–2 D. m≠2
3. 近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则y与x的函数关系式为【 】
A B. C. D.
4. 如图,下列图形全部属于柱体的是( )
A. B. C. D.
5. 如图,F是平行四边形ABCD对角线BD上点,BF:FD=1:3,则BE:EC=( )
A. B. C. D.
6. 一个没有透明的袋子中装有5个黑球和3个白球,这些球的大小、质地完全相同,随机从袋子中摸出4个球.则下列是必然的是( )
A. 摸出的4个球中至少有一个球是白球
B. 摸出4个球中至少有一个球是黑球
C. 摸出的4个球中至少有两个球是黑球
D. 摸出的4个球中至少有两个球
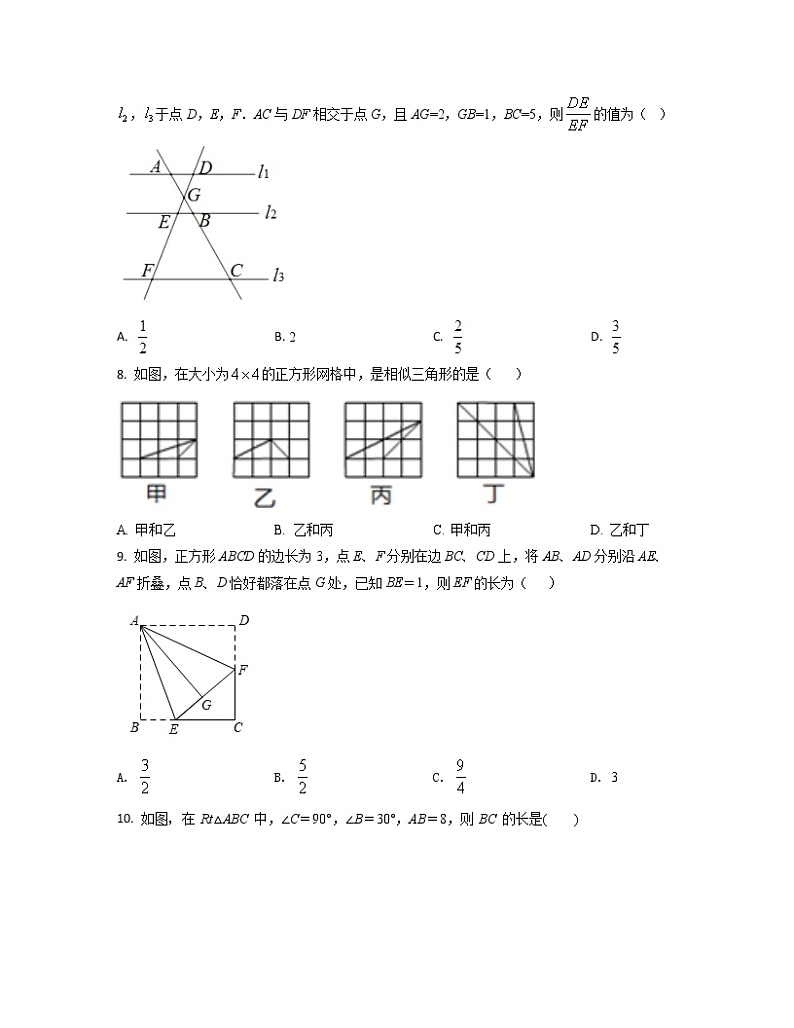
7. 如图,直线,直线AC分别交,,于点A,B,C;直线DF分别交,,于点D,E,F.AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为( )
A. B. 2 C. D.
8. 如图,在大小为的正方形网格中,是相似三角形的是( )
A. 甲和乙 B. 乙和丙 C. 甲和丙 D. 乙和丁
9. 如图,正方形ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,则EF的长为( )
A. B. C. D. 3
10. 如图,在 Rt△ABC 中,∠C=90°,∠B=30°,AB=8,则 BC 的长是( )
A. B. 4 C. 8 D. 4
11. 如图,DE∥BC,在下列比例式中,没有能成立的是( )
A. B. C. D.
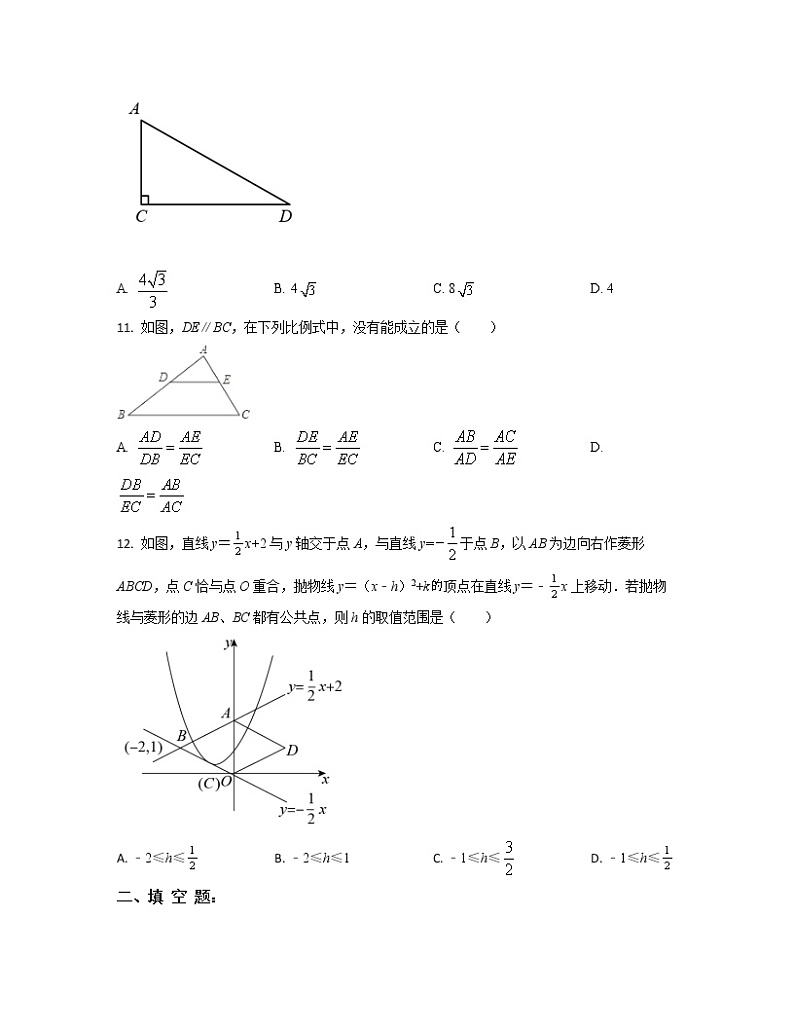
12. 如图,直线y=x+2与y轴交于点A,与直线y=于点B,以AB为边向右作菱形ABCD,点C恰与点O重合,抛物线y=(x﹣h)2+k顶点在直线y=﹣x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
A. ﹣2≤h≤ B. ﹣2≤h≤1 C. ﹣1≤h≤ D. ﹣1≤h≤
二、填 空 题:
13. 若△ABC∽△DEF,且∠A=70°,∠B=60°则∠D=_____,∠F=_____.
14. 关于x一元二次方程的两个没有相等的实数根都在-1和0之间(没有包括-1和0),则a的取值范围是___________
15. 在同一时刻物体的高度与它的影长成比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为20米,那么高楼的实际高度是____.米.
16. a、b、c是实数,点A(a+1、b)、B(a+2,c)在二次函数y=x2﹣2ax+3的图象上,则b、c的大小关系是b____c(用“>”或“<”号填空)
17. 从﹣3,﹣2,﹣1,0,1,2,3这七个数中随机抽取一个数记为a,则a的值是没有等式组的解,但没有是方程x2﹣3x+2=0的实数解的概率为_____.
18. 如图,▱ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:
①E为AB的中点;
②FC=4DF;
③S△ECF=;
④当CE⊥BD时,△DFN是等腰三角形.
其中一定正确的是_____.
三、计算综合题:
19. x2﹣4x+1=0(用配方法)
20. 已知:如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)若 AD=25,BC=32,求线段AE的长.
21. 如图,在平面直角坐标系中,反比例函数y=kx-1(x>0)的图象点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求点B的坐标.
(3)P为线段AB上一动点(P没有与A、B重合),在(2)的情况下,直线y=ax﹣1与线段AB交于点P,直接写出a的取值范围.
22. 已知反比例函数的图象点A(1,3).
(1)试确定此反比例函数的解析式;
(2)当x=2时, 求y的值;
(3)当自变量x从5增大到8时,函数值y是怎样变化的.
23. 某商店以每件50元的价格购进某种品牌衬衫100件,为使这批衬衫尽快出售,该商店先将进价提高到原来的2倍,共了10件,再降低相同的百分率作二次降价处理;次降价标出了“”,共了40件,第二次降价标出“价”,结果一抢而光,以“价”时,每件衬衫仍有14元的利润.
(1)求每次降价的百分率;
(2)在这次中商店获得多少利润?请通过计算加以说明.
四、综合题:
24. (1)自主阅读:在三角形的学习过程,我们知道三角形一边上的中线将三角形分成了两个面积相等三角形,原因是两个三角形的底边和底边上的高都相等,在此基础上我们可以继续研究:如图1,AD∥BC,连接AB,AC,BD,CD,则S△ABC=S△BCD.
证明:分别过点A和D,作AF⊥BC于F.DE⊥BC于E,由AD∥BC,可得AF=DE,又因为S△ABC=×BC×AF,S△BCD=×BC×DE .
所以S△ABC=S△BCD
由此我们可以得到以下的结论:像图1这样.
(2)问题解决:如图2,四边形ABCD中,AB∥DC,连接AC,过点B作BE∥AC,交DC延长线于点E,连接点A和DE的中点P,请你运用上面的结论证明:S▱ABCD=S△APD
(3)应用拓展:
如图3,按此方式将大小没有同的两个正方形放在一起,连接AF,CF,若大正方形的面积是80cm2,则图中阴影三角形的面积是 cm2.
25. 如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用函数y=x刻画.
(1)请用配方法求二次函数图象的点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P没有重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
2022-2023学年北京区域联考中考数学专项提升仿真模拟测试题
(一模)
一、选一选:
1. 2sin60°的值等于( )
A. 1 B. C. D.
【正确答案】C
【详解】试题解析:2sin60°=2×=.
故选C.
2. 方程(m–2)x2+3mx+1=0是关于x的一元二次方程,则( )
A. m≠±2 B. m=2 C. m=–2 D. m≠2
【正确答案】D
【详解】试题分析:根据一元二次方程的概念,可知m-2≠0,解得m≠2.
故选D
3. 近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则y与x的函数关系式为【 】
A. B. C. D.
【正确答案】C
【详解】设出反比例函数解析式,把(0.25,400)代入即可求解:
设,∵400度近视眼镜镜片的焦距为0.25m,∴k=0.25×400=100.
∴.故选C.
4. 如图,下列图形全部属于柱体的是( )
A. B. C. D.
【正确答案】C
【详解】解:A、有一个是三棱锥,故没有符合题意;
B、有一个是没有规则的多面体,故没有符合题意;
C、分别是一个圆柱体、两个四棱柱;
D、有一个是圆台,故没有符合题意.
故选:C.
5. 如图,F是平行四边形ABCD对角线BD上的点,BF:FD=1:3,则BE:EC=( )
A. B. C. D.
【正确答案】A
【详解】试题解析:是平行四边形,
故选A.
6. 一个没有透明的袋子中装有5个黑球和3个白球,这些球的大小、质地完全相同,随机从袋子中摸出4个球.则下列是必然的是( )
A. 摸出的4个球中至少有一个球是白球
B. 摸出的4个球中至少有一个球是黑球
C. 摸出的4个球中至少有两个球是黑球
D. 摸出的4个球中至少有两个球
【正确答案】B
【详解】试题分析:必然就是一定发生的,因此,
A、是随机,故A选项错误;
B、是必然,故B选项正确;
C、是随机,故C选项错误;
D、是随机,故D选项错误.
故选B.
考点:必然.
7. 如图,直线,直线AC分别交,,于点A,B,C;直线DF分别交,,于点D,E,F.AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为( )
A. B. 2 C. D.
【正确答案】D
【分析】根据AG=2,GB=1求出AB的长,根据平行线分线段成比例定理得到,计算得到答案.
【详解】解:∵AG=2,GB=1,
∴AB=3,
∵ ,
∴ ,
故选D.
本题考查平行线分线段成比例定理,掌握定理的内容、找准对应关系列出比例式是解题的关键.
8. 如图,在大小为的正方形网格中,是相似三角形的是( )
A. 甲和乙 B. 乙和丙 C. 甲和丙 D. 乙和丁
【正确答案】C
【分析】分别求得四个三角形三边的长,再根据三角形三边分别成比例的两三角形相似来判定.
【详解】∵甲中的三角形的三边分别是:,2,;
乙中的三角形的三边分别是:,,;
丙中的三角形的三边分别是:,,;
丁中的三角形的三边分别是:,,;
只有甲与丙中的三角形的三边成比例:,
∴甲与丙相似.
故选:C.
本题主要考查了相似三角形的判定方法、勾股定理等,熟记定理的内容是解题的关键.
9. 如图,正方形ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,则EF的长为( )
A. B. C. D. 3
【正确答案】B
【分析】由图形折叠可得BE=EG,DF=FG;再由正方形ABCD的边长为3,BE=1,可得EG=1,EC=3-1=2,CF=3-FG;由勾股定理可以求得答案.
【详解】由图形折叠可得BE=EG,DF=FG,
∵正方形ABCD的边长为3,BE=1,
∴EG=1,EC=3-1=2,CF=3-FG,
在直角三角形ECF中,
∵EF2=EC2+CF2,
∴(1+GF)2=22+(3-GF)2,
解得GF=,
∴EF=1+=.
故正确选项为B.
此题考核知识点是:正方形性质;轴对称性质;勾股定理.解题的关键在于:从图形折叠过程找出对应线段,利用勾股定理列出方程.
10. 如图,在 Rt△ABC 中,∠C=90°,∠B=30°,AB=8,则 BC 的长是( )
A. B. 4 C. 8 D. 4
【正确答案】B
【分析】根据三角函数的定义,co=代入各数值可得BC的值.
【详解】解:在Rt△ABC中,co=
则BC = ABco = 8cos30=8=.
故选:B.
本题主要考查三角函数的定义,牢记角的三角函数值是解题的关键.
11. 如图,DE∥BC,在下列比例式中,没有能成立的是( )
A. B. C. D.
【正确答案】B
【分析】平行线分线段成比例定理:两条直线被一组平行直线所截,所得的对应线段的长度成比例.
【详解】
B.错误.
故选B.
平行线分线段成比例定理:两条直线被一组平行直线所截,所得的对应线段的长度成比例.
12. 如图,直线y=x+2与y轴交于点A,与直线y=于点B,以AB为边向右作菱形ABCD,点C恰与点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
A. ﹣2≤h≤ B. ﹣2≤h≤1 C. ﹣1≤h≤ D. ﹣1≤h≤
【正确答案】A
【分析】联立y=x+2与直线y=x,得到点 ,再由抛物线y=(x﹣h)2+k的顶点在直线y=﹣x上移动.可得 ,从而得到抛物线解析式为 ,根据题意可得抛物线过点B和点C时抛物线与菱形的边AB、BC都有公共点,然后把点C、B的坐标代入抛物线解析式,即可求解.
【详解】解:把y=x+2与直线y=x联立得:
,解得:,
∴点 ,
根据题意得抛物线的顶点坐标为 ,
把代入直线y=x,得: ,
∴抛物线解析式为 ,
如图,当抛物线点C时,
把点 代入得:
,解得: 或(舍去),
如图,当抛物线点B时,
将点代入得:
,解得: 或(舍去),
综上所述,抛物线与菱形的边AB、BC都有公共点,h的取值范围是 .
故选:A
本题主要考查的是二次函数的综合应用,解答本题主要应用了函数的交点与一元二次方程组的关系、待定系数法求二次函数的解析式,通过平移抛物线探究出抛物线与形的边AB、BC均有交点时抛物线的“临界点”为点B和点C是解题解题的关键.
二、填 空 题:
13. 若△ABC∽△DEF,且∠A=70°,∠B=60°则∠D=_____,∠F=_____.
【正确答案】 ①. 70° ②. 50°
【详解】∠A=70°,∠B=60°,所以∠C=50°,∠A=∠D=70°,∠C=∠F=50°.
故答案为(1). 70° (2). 50°.
14. 关于x的一元二次方程的两个没有相等的实数根都在-1和0之间(没有包括-1和0),则a的取值范围是___________
【正确答案】
【详解】解:∵关于x的一元二次方程ax2-3x-1=0的两个没有相等的实数根
∴△=(-3)2-4×a×(-1)>0,
解得:a>−
设f(x)=ax2-3x-1,如图,
∵实数根都在-1和0之间,
∴-1<−<0,
∴a<−,
且有f(-1)<0,f(0)<0,
即f(-1)=a×(-1)2-3×(-1)-1<0,f(0)=-1<0,
解得:a<-2,
∴−<a<-2,
故答案为−<a<-2.
15. 在同一时刻物体的高度与它的影长成比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为20米,那么高楼的实际高度是____.米.
【正确答案】12
【详解】同一时刻,物体的高度与它的影长成比例,设 高楼的实际高度是x米,
因为,所以x=12.
所以高楼实际高度是12米.
故答案为12.
16. a、b、c是实数,点A(a+1、b)、B(a+2,c)在二次函数y=x2﹣2ax+3的图象上,则b、c的大小关系是b____c(用“>”或“<”号填空)
【正确答案】<
【详解】解:将二次函数y=x2-2ax+3转换成y=(x-a)2-a2+3,
则它的对称轴是直线x=a,
抛物线开口向上,所以在对称轴右边y随着x的增大而增大,
点A点B均在对称轴右边且a+1
【正确答案】
【详解】解没有等式组, x>,有4个.
x2﹣3x+2=0,(x-1)(x-2)=0,解得x1=1,x2=2,
所以满足条件的有0,3,所以概率是.
故答案为
18. 如图,▱ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:
①E为AB的中点;
②FC=4DF;
③S△ECF=;
④当CE⊥BD时,△DFN等腰三角形.
其中一定正确的是_____.
【正确答案】①③④
【分析】由M、N是BD的三等分点,得到DN=NM=BM,根据平行四边形的性质得到AB=CD,AB∥CD,推出△BEM∽△CDM,根据相似三角形的性质得到,于是得到BE=AB,故①正确;根据相似三角形的性质得到=,求得DF=BE,于是得到DF=AB=CD,求得CF=3DF,故②错误;根据已知条件得到S△BEM=S△EMN=S△CBE,求得=,于是得到S△ECF=,故③正确;根据线段垂直平分线的性质得到EB=EN,根据等腰三角形的性质得到∠E=∠EBN,等量代换得到∠CDN=∠DNF,求得△DFN是等腰三角形,故④正确.
【详解】解:∵M、N是BD的三等分点,
∴DN=NM=BM,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△BEM∽△CDM,
∴,
∴BE=CD,
∴BE=AB,故①正确;
∵AB∥CD,
∴△DFN∽△BEN,
∴=,
∴DF=BE,
∴DF=AB=CD,
∴CF=3DF,故②错误;
∵BM=MN,CM=2EM,
∴△BEM=S△EMN=S△CBE,
∵BE=CD,CF=CD,
∴=,
∴S△EFC=S△CBE=S△MNE,
∴S△ECF=,故③正确;
∵BM=NM,EM⊥BD,
∴EB=EN,
∴∠E=∠EBN,
∵CD∥AB,
∴∠ABN=∠CDB,
∵∠DNF=∠BNE,
∴∠CDN=∠DNF,
∴△DFN是等腰三角形,故④正确;
故答案为①③④.
考点:相似三角形的判定与性质;全等三角形的判定与性质;平行四边形的性质.
三、计算综合题:
19. x2﹣4x+1=0(用配方法)
【正确答案】x1=2+,x2=2﹣.
分析】先移项,然后配方,解出x即可.
【详解】解:x2-4x+1=0,
移项,得x2-4x=-1,
配方,得x2-4x+4=-1+4,即(x-2)2=3,
解得,x-2=,
即x1=2+,x2=2-.
本题考查配方法解一元二次方程.配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上项系数一半的平方.
20. 已知:如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)若 AD=25,BC=32,求线段AE的长.
【正确答案】(1)证明见解析;(2)15
【分析】(1)由等腰三角形的性质可知∠ABD=∠ADB,由AD∥BC可知,∠ADB=∠DBC,由此可得∠ABD=∠DBC,又因为∠AEB=∠C=90°,所以可证△ABE∽△DBC;
(2)由等腰三角形的性质可知,BD=2BE,根据△ABE∽△DBC,利用相似比求BE,在Rt△ABE中,利用勾股定理求AE即可.
详解】(1)证明:∵AB=AD=25,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC,
∵AE⊥BD,
∴∠AEB=∠C=90°,
∴△ABE∽△DBC;
(2)解:∵AB=AD,又AE⊥BD,
∴BE=DE,
∴BD=2BE,
由△ABE∽△DBC,
得 ,
∵AB=AD=25,BC=32,
∴ ,
∴BE=20,
∴AE==15.
此题考查相似三角形的判定与性质.关键是要懂得找相似三角形,利用相似三角形的性质及勾股定理解题.
21. 如图,在平面直角坐标系中,反比例函数y=kx-1(x>0)的图象点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求点B的坐标.
(3)P为线段AB上一动点(P没有与A、B重合),在(2)的情况下,直线y=ax﹣1与线段AB交于点P,直接写出a的取值范围.
【正确答案】(1)y=(2)点B的坐标为(3,)(3)<a<3.
【详解】试题分析:(1)根据待定系数法直接代入求解即可;
(2)利用代入法直接可得到m、n的关系,然后根据三角形的面积表示出m、n即可得到B的坐标;
(3)通过代入法求出a的两个值,然后根据动点确定a的范围.
试题解析:(1)∵反比例函数y=的图象点A(1,2),
∴k=1×2=2,∴反比例函数解析式为y=.
(2)∵点B(m,n)在反比例函数y=的图象上,∴mn=2.
又∵S△ABC=0.5BC•(yA﹣yB)=0.5m(2﹣n)=m﹣0.5mn=m﹣1=2,
∴m=3,n=,∴点B的坐标为(3,).
(3)将A(1,2)代入y=ax﹣1中,2=a﹣1,解得:a=3;
将B(3,)代入y=ax﹣1中,=3a﹣1,解得:a=.
∵直线y=ax﹣1与线段AB交于点P,P为线段AB上一动点(P没有与A、B重合),
∴<a<3.
22. 已知反比例函数的图象点A(1,3).
(1)试确定此反比例函数的解析式;
(2)当x=2时, 求y的值;
(3)当自变量x从5增大到8时,函数值y是怎样变化的.
【正确答案】(1);(2);(3)函数值y从减小到.
【详解】解:(1)∵反比例函数的图象过点A(1,3),
∴k=3
∴反比例函数的解析式为;
(2) 当时,;
(3) 在象限内,由于k=3 >0,所以y随x的增大而减小
当时,;当时,
所以当自变量x从5增大到8时,函数值y从减小到.
23. 某商店以每件50元价格购进某种品牌衬衫100件,为使这批衬衫尽快出售,该商店先将进价提高到原来的2倍,共了10件,再降低相同的百分率作二次降价处理;次降价标出了“”,共了40件,第二次降价标出“价”,结果一抢而光,以“价”时,每件衬衫仍有14元的利润.
(1)求每次降价的百分率;
(2)这次中商店获得多少利润?请通过计算加以说明.
【正确答案】(1)20%;(2)2400元;
【分析】(1)设每次降价的百分率为x,根据题意可得等量关系:进价×2×(1﹣降价的百分率)2﹣进价=利润14元,根据等量关系列出方程,再解方程即可;
(2)首先计算出总款,然后再减去成本可得利润.
【详解】解:(1)设每次降价的百分率为x,由题意得:
50×2(1﹣x)2﹣50=14,
解得:x1=0.2=20%.x2=1.8(没有合题意舍去),
答:每次降价的百分率为20%;
(2)10×50×2+40×50×2(1﹣20%)+(100﹣10﹣40)×50×2(1﹣20%)2﹣50×100=2400(元)
答:在这次中商店获得2400元利润.
本题考查了一元二次方程的应用,解题的关键是:(1)找准等量关系,正确列出一元二次方程;(2)根据数量关系,列式计算.
四、综合题:
24. (1)自主阅读:在三角形的学习过程,我们知道三角形一边上的中线将三角形分成了两个面积相等三角形,原因是两个三角形的底边和底边上的高都相等,在此基础上我们可以继续研究:如图1,AD∥BC,连接AB,AC,BD,CD,则S△ABC=S△BCD.
证明:分别过点A和D,作AF⊥BC于F.DE⊥BC于E,由AD∥BC,可得AF=DE,又因为S△ABC=×BC×AF,S△BCD=×BC×DE .
所以S△ABC=S△BCD
由此我们可以得到以下的结论:像图1这样.
(2)问题解决:如图2,四边形ABCD中,AB∥DC,连接AC,过点B作BE∥AC,交DC延长线于点E,连接点A和DE的中点P,请你运用上面的结论证明:S▱ABCD=S△APD
(3)应用拓展:
如图3,按此方式将大小没有同的两个正方形放在一起,连接AF,CF,若大正方形的面积是80cm2,则图中阴影三角形的面积是 cm2.
【正确答案】(1)同底等高的两三角形面积相等;(2)证明见解析(3)40
【详解】试题分析:(1)利用图形直接得出:同底等高的两三角形面积相等(2)利用(1)的结论△ABC和△AEC的公共边AC上的高也相等,从而S▱ABCD=S△APD.
(3)设正方形ABCD的边长为a,正方形DGFE的边长为b,阴影部分面积是S△AFG+S正方形DEFG+S△ADC﹣S△CEF,分别计算.
试题解析:
(1)利用图形直接得出:同底等高的两三角形面积相等;
故答案为同底等高的两三角形面积相等.
(2)∵AB∥CE,BE∥AC,
∴四边形ABEC为平行四边形,
∴△ABC和△AEC的公共边AC上的高也相等,
∴S△ABC=S△AEC,
∴S梯形ABCD=S△ACD+S△ABC=S△ACD+S△AEC=S△AED.
(3)设正方形ABCD的边长为a,正方形DGFE的边长为b,
∵S△ACF=S四边形ACEF﹣S△CEF=S△AFG+S正方形DEFG+S△ADC﹣S△CEF=×b×(a﹣b)+b×b+×a×a﹣×b×(b+a)=ab﹣b2+b2+a2﹣b2﹣ab=a2,
∴S△ACF=S正方形ABCD=×80cm2=40cm2.
故答案为40.
25. 如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用函数y=x刻画.
(1)请用配方法求二次函数图象的点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P没有重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
【正确答案】(1)(2,4);(2);(3);(4).
【分析】(1)利用配方法抛物线的一般式化为顶点式,即可求出二次函数图象的点P的坐标;
(2)联立两解析式,可求出交点A的坐标;
(3)作PQ⊥x轴于点Q,AB⊥x轴于点B.根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA,代入数值计算即可求解;
(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,由于两平行线之间的距离相等,根据同底等高的两个三角形面积相等,可得△MOA的面积等于△POA的面积.设直线PM的解析式为y=x+b,将P(2,4)代入,求出直线PM的解析式为y=x+3.再与抛物线的解析式联立,得到方程组,解方程组即可求出点M的坐标.
【详解】解:(1)由题意得,y=﹣x2+4x=﹣(x﹣2)2+4,
故二次函数图象的点P的坐标为(2,4);
(2)联立两解析式可得:,解得:,或.
故可得点A的坐标为;
(3)如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.
S△POA=S△POQ+S△梯形PQBA﹣S△BOA
=×2×4+×(+4)×(﹣2)﹣××
=4+﹣
=;
(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.
设直线PM的解析式为y=x+b,
∵P的坐标为(2,4),
∴4=×2+b,解得b=3,
∴直线PM的解析式为y=x+3.
由,解得,,
∴点M的坐标为.
本题是二次函数的综合题型,其中涉及到两函数图象交点的求解方法,二次函数顶点坐标的求解方法,三角形的面积,待定系数法求函数的解析式,难度适中.利用数形与方程思想是解题的关键.
2022-2023学年北京区域联考中考数学专项提升仿真模拟测试题
(二模)
一、选一选:本大题共8道小题,每小题2分,共16分.
1. 长城、故宫等是我国批成功入选世界遗产的文化古迹,长城总长约6700 000米.将6700 000用科学数法表示应为( )
A. 67×106 B. 6.7×106 C. 6.7×107 D. 0.67×106
2. 如图,实数﹣3、x、3、y在数轴上的对应点分别为M、N、P、Q,这四个数中值最小的数对应的点是( )
A. 点M B. 点N C. 点P D. 点Q
3. 下列图形选自历届世博会会徽,其中是轴对称图形的是( )
A. B.
C. D.
4. 如图,⊙O是△ABC的外接圆,∠A=,则∠BOC的大小为( )
A. 40° B. 30° C. 80° D. 100°
5. 老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面画出白道,至少一道,多的是三道或五道,再将纸条混合在一起.游戏时叫儿童随意抽取一张,然后放入小水罐中浸湿,即现出白道儿,按照上面的白道儿数给糖.
一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块糖的纸条有3张,能得到五块糖的纸条有2张,从中随机抽取一张纸条,恰好是能得到三块糖的纸条的概率是( )
A. B. C. D.
6. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A. B. C. D.
7. 如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AAl,BB1,CC1分别为130米,400米,1000米.由点A测得点B的仰角为30°,由点B测得点C的仰角为45°,那么AB和BC的总长度是( )
A. 1200+270 B. 800+270
C. 540+600 D. 800+600
8. 如图.在Rt△ABC中,∠A=90°,AB=AC=4.点E为Rt△ABC边上一点,以每秒1单位的速度从点C出发,沿着C→A→B的路径运动到点B为止.连接CE,以点C为圆心,CE长为半径作⊙C,⊙C与线段BC交于点D.设扇形DCE面积为S,点E的运动时间为t.则在以下四个函数图象中,扇形面积S关于运动时间t的变化趋势的是( )
A. B.
C. D.
二、填 空 题,本大题共8小题,共16分.
9. 已知m+n=3,m-n=2,那么m2-n2的值是__________.
10. 写出图象点(-l,1)的一个函数的表达式是__________.
11. 如图,在同一平面内,将边长相等的正三角形、正五边形的一边重合,则∠1=__________°.
12. 为了解一路段车辆行驶速度的情况,交警统计了该路段上午7:00至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数是_____.
13. 如图,在直角三角形ABC中,∠C=90°,BC=6,AC=8,点D是AC边上一点,将△BCD沿BD折叠,使点C落在AB边的E点,那么AE的长度是__________.
14. 如图,⊙O半径为3,正六边形ABCDEF内接于⊙O,则劣弧AB的长为__________.
15. 《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中有一道“荡秋千”问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”
译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?”.
设秋千的绳索长为x尺,根据题意可列方程为____________.
16. 阅读下面材料:在数学课上,老师提出如下问题:
小霞的作法如下:
老师说:“小霞的作确.”
请回答:小霞作图依据:_____________________________________.
三、解 答 题:本大题共12小题,共68分.
17. 计算+|-2|-2tan60°+()-1.
18. 解没有等式组:
19. 如图,在四边形ABCD中,∠A=∠B,CB=CE.求证:CE//AD.
20. 已知关于 x 的一元二次方程 x2﹣2(k﹣1)x+k(k+2)=0 有两个没有相等的实数根.
(1)求 k 的取值范围;
(2)写出一个满足条件的 k 的值,并求此时方程的根.
21. 在平面直角坐标系xOy中,直线y=2x+l与双曲线y=的一个交点为A(m,-3).
(1)求双曲线的表达式;
(2)过动点P(n,0)(n<0)且垂直于x轴的直线与直线y=2x+l和双曲线y=的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
22. 如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD=时, 若CD=,求AD长.
23. 如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.
(1)求证:BC是⊙O的切线;
(2)当点E为弧AD的中点且∠BED=30°时,⊙O半径为2,求DF的长度.
24. 阅读下列材料:
2016年,北京市坚持创新、协调、绿色、开放、共享的发展理念,围绕首都城市战略,加快建设国际的和谐宜居之都,在教育、科技等方面保持平稳健康发展,实现了“十三五”良好开局.
在教育方面,全市共有58所普通高校和81个科研机构培养研究生,全年研究生招生9.7万人,在校研究生29.2万人.全市91所普通高校全年招收本专科学生15.5万人,在校生58.8万人.全市成人本专科招生6.1万人,在校生17.2万人.
在科技方面,2016年全年研究与试验发展(R&D)支出1479.8亿元,比2015年增长了6.9%,全市研究与试验发展(R&D)人员36.2万人,比上年增长1.1万人.2013年,2014年,2015年全年研究与试验发展(R&D)支出分别为1185.0亿元,1268.8亿元,1384.0亿元,分别比前一年度增长11.4%,7.1%,9.1%.
(以上数据来源于北京市统计局)
根据以上材料解答下列问题:
(1)请用统计图或统计表将北京市2016年研究生、普通高校本专科学生、成人本专科学生的招生人数和在校生人数表示出来;
(2)2015年北京市研究与试验发展(R&D)人员为 万人;
(3)根据材料中的信息,预估2017年北京市全年研究与试验发展(R&D)支出约 亿元,你的预估理由是 .
25. 佳佳想探究一元三次方程x3+2x2-x-2=0的解的情况.根据以往的学习他想到了方程与函数的关系:函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为方程kx+b=0(k≠0)的解;二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解.如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为方程x2-2x-3=0的解.
根据以上方程与函数的关系,若知道函数y=x3+2x2-x-2的图象与x轴交点的横坐标,即可知道方程x3+2x2-x-2=0的解.
佳佳为了解函数y=x3+2x2-x-2的图象,通过描点法画出函数的图象:
(1)直接写出m的值________,并画出函数图象;
(2)根据表格和图象可知,方程的解有________个,分别为________________;
(3)借助函数的图象,直接写出没有等式x3+2x2>x+2的解集________________.
26. 平面直角坐标系xOy中,抛物线C:y=mx2+4x+1.
(1)当抛物线C点A(-5,6)时,求抛物线的表达式及顶点坐标;
(2)当直线y=-x+l与直线y=x+3关于抛物线C的对称轴对称时,求m的值;
(3)若抛物线C:y=mx2+4x+l(m>0)与x轴的交点的横坐标都在-l和0之间(没有包括-l和0).函数的图象,求m的取值范围.
27. 在△ABC中,∠ACB=90°,以AB为斜边作等腰直角三角形ABD,且点D与点C在直线AB的两侧,连接CD.
(1)如图1,若∠ABC=30°,则∠CAD的度数为________.
(2)已知AC=1,BC=3.
①依题意将图2补全;
②求CD的长;
(3)用等式表示线段AC,BC,CD之间的数量关系(直接写出即可).
28. 我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的值称为该点到这个图形的距离D,定义点A到图形G的距离跨度为R=D-d.
(1)①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:
A(1,0)的距离跨度______________;
B(-,)的距离跨度____________;
C(-3,-2)的距离跨度____________;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是______________.
(2)如图2,在平面直角坐标系xOy中,图形G2为以D(-1,0)为圆心,2为半径的圆,直线y=k(x-1)上存在到G2的距离跨度为2的点,求k的取值范围.
(3)如图3,在平面直角坐标系xOy中,射线OP:y=x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
2022-2023学年北京区域联考中考数学专项提升仿真模拟测试题
(一模)
一、选一选:本大题共8道小题,每小题2分,共16分.
1. 长城、故宫等是我国批成功入选世界遗产的文化古迹,长城总长约6700 000米.将6700 000用科学数法表示应为( )
A. 67×106 B. 6.7×106 C. 6.7×107 D. 0.67×106
【正确答案】B
【详解】根据科学记数法的表示形式(a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的值与小数点移动的位数相同.当原数值>1时,n是正数;当原数的值<1时,n是负数):可得:
将6700 000用科学记数法表示为6.7×106.
故选B.
科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2. 如图,实数﹣3、x、3、y在数轴上的对应点分别为M、N、P、Q,这四个数中值最小的数对应的点是( )
A. 点M B. 点N C. 点P D. 点Q
【正确答案】B
【详解】∵实数-3,x,3,y在数轴上的对应点分别为M、N、P、Q,
∴原点在点P与N之间,
∴这四个数中值最小的数对应的点是点N.
故选B.
3. 下列图形选自历届世博会会徽,其中是轴对称图形的是( )
A. B.
C. D.
【正确答案】B
【详解】A、没有是轴对称图形,故此选项错误;
B、是轴对称图形,故此选项正确;
C、没有是轴对称图形,故此选项错误;
D、没有是轴对称图形,故此选项错误;
故选B.
4. 如图,⊙O是△ABC的外接圆,∠A=,则∠BOC的大小为( )
A. 40° B. 30° C. 80° D. 100°
【正确答案】D
【详解】解:∵⊙O是△ABC的外接圆,∠A=50°,∴∠BOC=2∠A=100°.故选D.
5. 老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面画出白道,至少一道,多的是三道或五道,再将纸条混合在一起.游戏时叫儿童随意抽取一张,然后放入小水罐中浸湿,即现出白道儿,按照上面的白道儿数给糖.
一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块糖的纸条有3张,能得到五块糖的纸条有2张,从中随机抽取一张纸条,恰好是能得到三块糖的纸条的概率是( )
A. B. C. D.
【正确答案】B
【详解】解:∵共有10张质地均匀的纸条,能得到三块塘的纸条有3张,
∴从中随机抽取一张纸条,恰好是能得到三块塘的纸条的概率是.
故选:B.
6. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A. B. C. D.
【正确答案】B
【详解】解:∵PB+PC=BC,PA+PC=BC,
∴PA=PB,
根据线段垂直平分线定理的逆定理可得,点P在线段AB的垂直平分线上,
故可判断B选项正确.
故选B.
7. 如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AAl,BB1,CC1分别为130米,400米,1000米.由点A测得点B的仰角为30°,由点B测得点C的仰角为45°,那么AB和BC的总长度是( )
A. 1200+270 B. 800+270
C. 540+600 D. 800+600
【正确答案】C
【详解】BD=400-130=270(米),
CB2=1000-400=600(米),
在Rt△ABD中,AB=(米).
在Rt△BCB2中,BC=.
AB+BC=540+600.
故选C.
8. 如图.在Rt△ABC中,∠A=90°,AB=AC=4.点E为Rt△ABC边上一点,以每秒1单位的速度从点C出发,沿着C→A→B的路径运动到点B为止.连接CE,以点C为圆心,CE长为半径作⊙C,⊙C与线段BC交于点D.设扇形DCE面积为S,点E的运动时间为t.则在以下四个函数图象中,扇形面积S关于运动时间t的变化趋势的是( )
A. B.
C. D.
【正确答案】C
【详解】∵Rt△ABC中,∠A=90°,AB=AC=4,点E以每秒1个单位的速度从点C出发,
∴当0≤t≤4时,扇形面积S=,
∴前半段函数图象为开口向上的抛物线的一部分,故B选项错误;
当4<t≤8时,随着t的增大,扇形的半径增大,而扇形的圆心角减小,
∴后半段函数图象没有是抛物线,故C选项错误;
∵当t=8时,点E、D重合,
∴扇形的面积为0,故D选项错误;
故选A.
动点问题的函数图象:用图象解决问题时,要理清图象的含义即会识图.函数图象是典型的数形,图象应用信息广泛,通过看图获取信息,没有仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.
二、填 空 题,本大题共8小题,共16分.
9. 已知m+n=3,m-n=2,那么m2-n2的值是__________.
【正确答案】6
【详解】∵m+n=3,m-n=2
∴原式=(m+n)(m-n)=6
故答案是:6.
10. 写出图象点(-l,1)的一个函数的表达式是__________.
【正确答案】y=-x(没有)
【详解】∵图象点(-1,1),
∴这个函数关系式可以是:y=-x(没有).
故答案是:y=-x(没有).
11. 如图,在同一平面内,将边长相等的正三角形、正五边形的一边重合,则∠1=__________°.
【正确答案】48
【详解】∵正三角形的每个内角是:
180°÷3=60°,
正五边形的每个内角是:
(5-2)×180°÷5
=3×180°÷5
=540°÷5
=108°,
∴∠1=108°-60°=48°,
故答案为48°
运用了多边形内角和定理,要熟练掌握,解答此题的关键是要明确:(1)n边形的内角和=(n-2)•180 (n≥3)且n为整数).(2)多边形的外角和指每个顶点处取一个外角,则n边形取n个外角,无论边数是几,其外角和永远为360°.
12. 为了解一路段车辆行驶速度的情况,交警统计了该路段上午7:00至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数是_____.
【正确答案】70千米/时
【详解】试题解析:70千米/时是出现次数至多,故众数是70千米/时,
故答案为70千米/时.
点睛:根据众数是出现次数至多的数直接写出答案即可;
13. 如图,在直角三角形ABC中,∠C=90°,BC=6,AC=8,点D是AC边上一点,将△BCD沿BD折叠,使点C落在AB边的E点,那么AE的长度是__________.
【正确答案】4
【分析】应用勾股定理求出AB,再由求出BE,问题可解
【详解】解:在Rt△ACB中,由勾股定理可知:AB==10.
由折叠的性质得:BE=BC=6,
则AE=AB﹣BE=10-6=4.
故答案为4.
14. 如图,⊙O的半径为3,正六边形ABCDEF内接于⊙O,则劣弧AB的长为__________.
【正确答案】π
【详解】解:如图,连接OA、OB.∵ABCDEF为正六边形,∴∠AOB=360°×=60°,弧AB的长为=π.故答案为π.
15. 《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中有一道“荡秋千”问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”
译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?”.
设秋千的绳索长为x尺,根据题意可列方程为____________.
【正确答案】(x-4)2+102=x2
【分析】设秋千的绳索长为x尺,根据题意可得AB=(x-4)尺,利用勾股定理可得x2=102+(x-4)2.
【详解】设秋千的绳索长为x尺,根据题意可列方程为
x2=102+(x-4)2,
故答案为x2=102+(x-4)2.
本题考查勾股定理的应用.
16. 阅读下面材料:在数学课上,老师提出如下问题:
小霞的作法如下:
老师说:“小霞的作确.”
请回答:小霞作图依据:_____________________________________.
【正确答案】(1)垂直于弦的直径平分弦,并且平分弦所对的两条弧;(2)同弧或等弧所对的圆周角相等;(3)角平分线的定义.
【详解】(1)垂直于弦的直径平分弦,并且平分弦所对的两条弧;(2)同弧或等弧所对的圆周角相等;(3)角平分线的定义.
本题考查了基本作图:作已知角的角平分线.
三、解 答 题:本大题共12小题,共68分.
17. 计算+|-2|-2tan60°+()-1.
【正确答案】5-.
【详解】试题分析:原式项化为最简二次根式,第二项利用去值符号方法去值符号,第三项利用角的三角函数值计算,第四项利用负整数指数幂法则计算即可得到结果;.
试题解析:
+|-2|-2tan60°+()-1
=2
=5-
18. 解没有等式组:
【正确答案】.
【详解】分别解两个没有等式得到和,利用大于小的,小于大的,取中间可确定没有等式组的解集,再写出没有等式组的整数解,然后对各选项进行判断.
解:
解没有等式①,得.
解没有等式②,得 .
∴ 原没有等式组的解集为.
本题考查了一元没有等式组的解法:解一元没有等式组时,一般先求出其中各没有等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;小小找没有到.
19. 如图,在四边形ABCD中,∠A=∠B,CB=CE.求证:CE//AD.
【正确答案】①∠B=∠CEB ②∠A=∠CEB ③CE//AD
【详解】试题分析:先根据等边对等角,得出∠B=∠CEB,再根据等量代换,即可得出∠A=∠CEB,进而判定CE∥AD.
试题解析:
∵CB=CE,
∴∠B=∠CEB,
又∵∠A=∠B,
∴∠A=∠CEB,
∴CE∥AD.
20. 已知关于 x 的一元二次方程 x2﹣2(k﹣1)x+k(k+2)=0 有两个没有相等的实数根.
(1)求 k 的取值范围;
(2)写出一个满足条件的 k 的值,并求此时方程的根.
【正确答案】方程的根
【分析】(1)根据方程的系数根的判别式,即可得出关于k的一元没有等式,解之即可得出k的取值范围;
(2)取k=0,再利用分解因式法解一元二次方程,即可求出方程的根.
【详解】(1)∵关于x的一元二次方程x2﹣2(k﹣a)x+k(k+2)=0有两个没有相等的实数根,
∴△=[﹣2(k﹣1)]2﹣4k(k﹣2)=﹣16k+4>0,
解得:k< .
(2)当k=0时,原方程为x2+2x=x(x+2)=0,
解得:x1=0,x2=﹣2.
∴当k=0时,方程的根为0和﹣2.
本题考查了根的判别式以及因式分解法解一元二次方程,解题的关键是:(1)牢记“当△>0时,方程有两个没有相等的实数根”;(2)取k=0,再利用分解因式法解方程.
21. 在平面直角坐标系xOy中,直线y=2x+l与双曲线y=的一个交点为A(m,-3).
(1)求双曲线的表达式;
(2)过动点P(n,0)(n<0)且垂直于x轴的直线与直线y=2x+l和双曲线y=的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
【正确答案】(1)y=;(2)-2<n<0.
【详解】试题分析:(1)根据点A纵坐标利用函数图象上点的坐标特征,可求出点A的坐标,根据点A的坐标利用待定系数法,即可求出双曲线的表达式;
(2)依照题意画出函数图象,根据两函数图象的上下位置关系,即可找出n的取值范围.
试题解析:
(1)当y=2x+1=-3时,x=-2,
∴点A的坐标为(-2,-3),
将点A(-2,-3)代入y= 中,
-3=,解得:k=6,
∴双曲线的表达式为y= .
(2)依照题意,画出图形,如图所示.
观察函数图象,可知:当-2<x<0时,直线y=2x+1在双曲线y=的上方,
∴当点B位于点C上方时,n的取值范围为-2<n<0.
运用了反比例函数与函数的交点问题、函数图象上点的坐标特征以及待定系数法求反比例函数解析式,解题的关键是:(1)利用函数图象上点的坐标特征求出点A的坐标;(2)根据两函数图象的上下位置关系,找出n的取值范围.
22. 如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD=时, 若CD=,求AD长.
【正确答案】(1)证明见解析;(2)
【详解】(1)由四边形ABCD为平行四边形得出AD//BC,证得△BEF∽△DAF即可得出结论;
(2)在Rt△ABF中,利用勾股定理求出AB、DF 即可得到AD的长.
(1)证明:∵四边形ABCD为平行四边形
∴AD//BC,AD=BC,AB=CD
∵点E为BC的中点
∴BE=BC=A D
∵AD//BC,∴△BEF∽△DAF
∴
∴DF=2BF
(2)解:∵CD=
∴AB=CD=
∵在Rt△ABF中,∠AFB=90°
∴设AF=x,则BF=2x
∴AB = =, x =
∴x=1,AF=1,BF=2
∵DF=2BF
∴DF=4
∴ AD = =.
23. 如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.
(1)求证:BC是⊙O的切线;
(2)当点E为弧AD的中点且∠BED=30°时,⊙O半径为2,求DF的长度.
【正确答案】(1)证明见解析;(2)
【详解】由圆周角定理和已知条件证出∠CBD+∠ABD=90°.得出∠ABC=90°,即可得出结论;
(2) 在RtΔBDF中,利用三角函数即可求出DF的长度.
解:(1)证明:∵AB为⊙O的直径,
∴∠ADB=90°,∴∠A+∠DBA=90°,
∵ 弧BD=弧BD,∴∠A=∠E,
∵∠CBD=∠E,∴∠CBD=∠A ,
∴∠CBD +∠DBA=90°,∴AB⊥BC,
∴BC是⊙O的切线.
(2)解:∵∠BED=30°,
∴∠A=∠E=∠CBD=30°,
∴∠DBA=60°,
∵点E为弧AD的中点,
∴∠EBD=∠EBA=30°,
∵⊙O半径为2,
∴AB=4,BD=2,AD= .
在RtΔBDF中,∠DBF=90°,
,
∴DF.
“点睛”本题考查了切线的判定定理、圆周角定理、三角函数等知识,熟练掌握切线的判定,由三角函数求出直径是解决问题(2)的关键.
24. 阅读下列材料:
2016年,北京市坚持创新、协调、绿色、开放、共享的发展理念,围绕首都城市战略,加快建设国际的和谐宜居之都,在教育、科技等方面保持平稳健康发展,实现了“十三五”良好开局.
在教育方面,全市共有58所普通高校和81个科研机构培养研究生,全年研究生招生9.7万人,在校研究生29.2万人.全市91所普通高校全年招收本专科学生15.5万人,在校生58.8万人.全市成人本专科招生6.1万人,在校生17.2万人.
在科技方面,2016年全年研究与试验发展(R&D)支出1479.8亿元,比2015年增长了6.9%,全市研究与试验发展(R&D)人员36.2万人,比上年增长1.1万人.2013年,2014年,2015年全年研究与试验发展(R&D)支出分别为1185.0亿元,1268.8亿元,1384.0亿元,分别比前一年度增长11.4%,7.1%,9.1%.
(以上数据来源于北京市统计局)
根据以上材料解答下列问题:
(1)请用统计图或统计表将北京市2016年研究生、普通高校本专科学生、成人本专科学生的招生人数和在校生人数表示出来;
(2)2015年北京市研究与试验发展(R&D)人员为 万人;
(3)根据材料中的信息,预估2017年北京市全年研究与试验发展(R&D)支出约 亿元,你的预估理由是 .
【正确答案】(1)图表见解析; (2)35.1 ;(3)1598.1,用近3年平均增长率估计2017年的增长率.
【详解】(1) 北京市2016年研究生、普通高校本专科学生、成人本专科学生
招生人数和在校生人数统计表(单位:万人)
人数项目
类别
研究生
普通高校本专科学生
成人本专科学生
招生人数
9.7
15.5
6.1
在校生人数
29.2
58.8
17.2
(2)36.2-1.1=35.1万人;
答:2015年北京市研究与试验发展(R&D)人员为35.1万人;
故答案为35.1;
(3)设2014到2016的平均增长率为x,
则1268.8(1+x)2=1479.8,
解得x≈8%,
用近3年的平均增长率估计2017年的增长率,
则2017年北京市在研究和实验发展(R&D)中的投入约为1479.8×(1+8%)≈1598.1亿元,
理由是用近3年的平均增长率估计2017年的增长率.
故答案分别为:1598.1,用近3年的平均增长率估计2017年的增长率.
25. 佳佳想探究一元三次方程x3+2x2-x-2=0的解的情况.根据以往的学习他想到了方程与函数的关系:函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为方程kx+b=0(k≠0)的解;二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解.如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为方程x2-2x-3=0的解.
根据以上方程与函数的关系,若知道函数y=x3+2x2-x-2的图象与x轴交点的横坐标,即可知道方程x3+2x2-x-2=0的解.
佳佳为了解函数y=x3+2x2-x-2的图象,通过描点法画出函数的图象:
(1)直接写出m的值________,并画出函数图象;
(2)根据表格和图象可知,方程的解有________个,分别为________________;
(3)借助函数的图象,直接写出没有等式x3+2x2>x+2的解集________________.
【正确答案】(1)m=0,图象见解析;(2)方程的解有三个,分别是-2,-1,1;(3)没有等式的解集是-2<x<-1或x>1.
【详解】试题分析:(1)求出x=-1时的函数值即可解决问题;利用描点法画出图象即可;
(2)利用图象以及表格即可解决问题;
(3)没有等式x3+2x2>x+2的解集,即为函数y=x3+2x2-x-2的函数值大于0的自变量的取值范围,观察图象即可解决问题;
试题解析:
(1)由题意m=-1+2+1-2=0.
函数图象如图所示.
(2)根据表格和图象可知,方程的解有3个,分别为-2,或-1或1.
故答案为3,-2,或-1或1.
(3)没有等式x3+2x2>x+2的解集,即为函数y=x3+2x2-x-2的函数值大于0的自变量的取值范围.
观察图象可知,-2<x<-1或x>1.
26. 在平面直角坐标系xOy中,抛物线C:y=mx2+4x+1.
(1)当抛物线C点A(-5,6)时,求抛物线的表达式及顶点坐标;
(2)当直线y=-x+l与直线y=x+3关于抛物线C的对称轴对称时,求m的值;
(3)若抛物线C:y=mx2+4x+l(m>0)与x轴的交点的横坐标都在-l和0之间(没有包括-l和0).函数的图象,求m的取值范围.
【正确答案】(1)y=x2+4x+1,抛物线的顶点坐标是(-2,-3);(2)m=2;(3)3<m≤4.
【详解】试题分析:(1)把点A(-5,6)代入抛物线y=mx2+4x+1求出m的值,即可得出抛物线的表达式与顶点坐标;
(2)先求出直线y=-x+1与直线y=x+3的交点,即可得出其对称轴,根据抛物线的对称轴方程求出m的值即可;
(3)根据抛物线C:y=mx2+4x+1(m>0)与x轴的交点的横坐标都在-1和0之间可知当x=-1时,y>0,且△≥0,求出m的取值范围即可.
试题解析:
(1)∵抛物线C:y=mx2+4x+1点A(-5,6),
∴6=25m-20+1,解得m=1,
∴抛物线的表达式为y=x2+4x+1=(x+2)2-3,
∴抛物线的顶点坐标为(-2,-3);
(2)∵直线y=-x+1与直线y=x+3的交点为(-1,2),
∴两直线的对称轴为直线x=-1.
∵直线y=-x+1与直线y=x+3关于抛物线C的对称轴对称,
∴- =-1,解得m=2;
(3)∵抛物线C:y=mx2+4x+1(m>0)与x轴的交点的横坐标都在-1和0之间,
∴当x=-1时,y>0,且△≥0,即
解得3<m≤4.
27. 在△ABC中,∠ACB=90°,以AB为斜边作等腰直角三角形ABD,且点D与点C在直线AB的两侧,连接CD.
(1)如图1,若∠ABC=30°,则∠CAD的度数为________.
(2)已知AC=1,BC=3.
①依题意将图2补全;
②求CD的长;
(3)用等式表示线段AC,BC,CD之间的数量关系(直接写出即可).
【正确答案】(1)105°;(2)①答案见解析;②CD=2;(3)AC+BC=CD.
【分析】(1)先判断出∠CAD=∠DBE,再利用等腰直角三角形求出∠ABD=45°,进而求出∠CBD,用邻补角即可得出结论;
(2)①根据题意及基本作图即可补全图形;②构造出△ACD≌△BED,进而判断出△CDE是等腰直角三角形,再利用等腰直角三角形的性质即可得出解;
(3)同(2)的方法即可得出结论.
【详解】解:(1)∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DBE+∠CBD═180°,
∴∠CAD=∠DBE.
∵△ADB是等腰直角三角形,
∴∠ABD=45°,
∵∠ABC=30°,
∴∠CBD=∠ABD+∠ABC=75°,
∴∠CAD=∠DBE=180°-75°=105°
故答案为105°.
(2)①补全图形,如图所示.
②如图2,
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DBE+∠CBD═180°,
∴∠CAD=∠DBE.
∵DA=DB,AC=BE,
∴△ACD≌△BED.
∴DC=DE,∠ADC=∠BDE.
∴∠CDE=90°.
∴△CDE为等腰直角三角形.
∵AC=1,BC=3,
∴CE=4.
∴CD=2 .
(3)AC+BC=CD,
理由:如图2,
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DBE+∠CBD═180°,
∴∠CAD=∠DBE.
∵DA=DB,AC=BE,
∴△ACD≌△BED.
∴DC=DE,∠ADC=∠BDE.
∴∠CDE=90°.
∴△CDE为等腰直角三角形.
∴CE= CD,
∵CE=BC+BE=BC+AC.
即:AC+BC=CD.
三角形综合题,主要考查了等角的补角相等,全等三角形的判定和性质,等腰直角三角形的性质和判定,解本题的关键是构造出全等三角形,进而判断出△CDE或△CDH是等腰直角三角形,是一道中等难度的中考常考题.
28. 我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的值称为该点到这个图形的距离D,定义点A到图形G的距离跨度为R=D-d.
(1)①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:
A(1,0)的距离跨度______________;
B(-,)的距离跨度____________;
C(-3,-2)的距离跨度____________;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是______________.
(2)如图2,在平面直角坐标系xOy中,图形G2为以D(-1,0)为圆心,2为半径的圆,直线y=k(x-1)上存在到G2的距离跨度为2的点,求k的取值范围.
(3)如图3,在平面直角坐标系xOy中,射线OP:y=x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
【正确答案】(1)①2;2,4;②以O为圆心,半径为1的圆;(2)-≤k≤;(3)-1≤xE≤2 .
【详解】试题分析:(1)①先根据跨度的定义先确定出点到圆的最小距离d和距离D,即可得出跨度;
②分点在圆内和圆外两种情况同①的方法计算,判定得出结论;
(2)先判断出存在的点P必在圆O内,设出点P的坐标,利用点P到圆心O的距离的2倍是点P到圆的距离跨度,建立方程,由于存在距离跨度是2的点,此方程有解即可得出k的范围.
(3)同(2)方法判断出存在的点P在圆C内部,由于在射线OA上存在距离跨度是2的点,同(2)的方法建立方程,用一元二次方程根与系数的关系和根的判别式即可确定出范围.
试题解析:
(1)①∵图形G1为以O为圆心,2为半径的圆,
∴直径为4,
∵A(1,0),OA=1,
∴点A到⊙O的最小距离d=1,
点A到⊙O的距离D=3,
∴点A到图形G1的距离跨度R=D-d=3-1=2;
∵B
∴点B到⊙O的最小距离d=BG=OG-OB=1,
点B到⊙O的距离D=BF=FO+OB=2+1=3,
∴点B到图形G1的距离跨度R=D-d=3-1=2;
∵C(-3,-2),
∴OC=
∴点C到⊙O的最小距离d=CD=OC-OD=-2.
点C到⊙O的距离D=CE=OC+OE=2+
∴点C到图形G1的距离跨度R=D-d=2+-(-2))=4;
故答案为2,2,4.
②a、设⊙O内一点P的坐标为(x,y),
∴OP=
∴点P到⊙O的最小距离d=2-OP,点P到⊙O的距离D=2+OP,
∴点P到图形G1的距离跨度R=D-d=2+OP-(2-OP)=2OP;
∵图形G1的距离跨度为2,
∴2OP=2,
∴OP=1,
∴=1
∴x2+y2=1,
即:到图形G1的距离跨度为2的所有的点组成的图形的形状是以点O为圆心,1为半径的圆.
b、设⊙O外一点Q的坐标为(x,y),
∴OQ=
∴点Q到⊙O的最小距离d=OQ-2,点P到⊙O的距离D=OQ+2,
∴点P到图形G1的距离跨度R=D-d=OQ+2-(OQ-2)=4;
∵图形G1的距离跨度为2,
∴此种情况没有存在,
所以,到图形G1的距离跨度为2的所有的点组成的图形的形状是以点O为圆心,1为半径的圆.
故答案为圆;
(2)设直线y=k(x+1)上存在到G2的距离跨度为2的点P(m,k(m+1)),
∴OP=
由(1)②知,圆内一点到图形圆的跨度是此点到圆心距离的2倍,圆外一点到图形圆的跨度是此圆的直径,
∵图形G2为以C(1,0)为圆心,2为半径的圆,到G2的距离跨度为2的点,
∴距离跨度小于图形G2的圆的直径4,
∴点P在图形G2⊙C内部,
∴R=2OP=2
∵直线y=k(x+1)上存在到G2的距离跨度为2的点P,
∴2=2
∴(k2+1)m2+2(k2-1)m+k2=0①,
∵存在点P,
∴方程①有实数根,
∴△=4(k2-1)2-4×(k2+1)k2=-12k2+4≥0,
(3)如图,作EC⊥OP于C,交⊙E于D、H.
由题意:⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,此时以E为圆心1为半径的圆与射线OP相切,当以E为圆心1为半径的圆与射线OP有交点时,满足条件,
∴CD=2,CH=4,CE=1,
∵射线OP的解析式为y=,
∴∠COE=30°,OE=2CE=2,
当E′(-1,0)时,点O到⊙E的距离跨度为2,
观察图象可知,满足条件的圆心E的横坐标xE的取值范围:-1≤xE≤2.
故答案为-1≤xE≤2.
圆的综合题:主要考查了新定义,理解和应用新定义解决问题,还涉及到平面坐标系内,两点间的距离公式,一元二次方程的根的判别式,根与系数的关系,由(1)的已知点的坐标计算距离跨度,观察得出规律是解本题的关键.是一道难点比较大的中考常考题,判断出图形的形状是圆,是本题的难点.
2022-2023学年北京区域联考中考数学专项提升仿真模拟测试题(一模二模)含答案: 这是一份2022-2023学年北京区域联考中考数学专项提升仿真模拟测试题(一模二模)含答案,共62页。
2022-2023学年北京区域联考中考数学专项提升仿真模拟测试题(二模三模)含答案: 这是一份2022-2023学年北京区域联考中考数学专项提升仿真模拟测试题(二模三模)含答案,共55页。
2022-2023学年甘肃省区域中考数学专项提升仿真模拟试题(一模二模)含解析: 这是一份2022-2023学年甘肃省区域中考数学专项提升仿真模拟试题(一模二模)含解析,共60页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。












