所属成套资源:2023年高考数学二轮复习重点基础练习
2023年高考数学二轮复习重点基础练习:专题十五 考点44 变量的相关性与统计案例(B卷)
展开这是一份2023年高考数学二轮复习重点基础练习:专题十五 考点44 变量的相关性与统计案例(B卷),共10页。
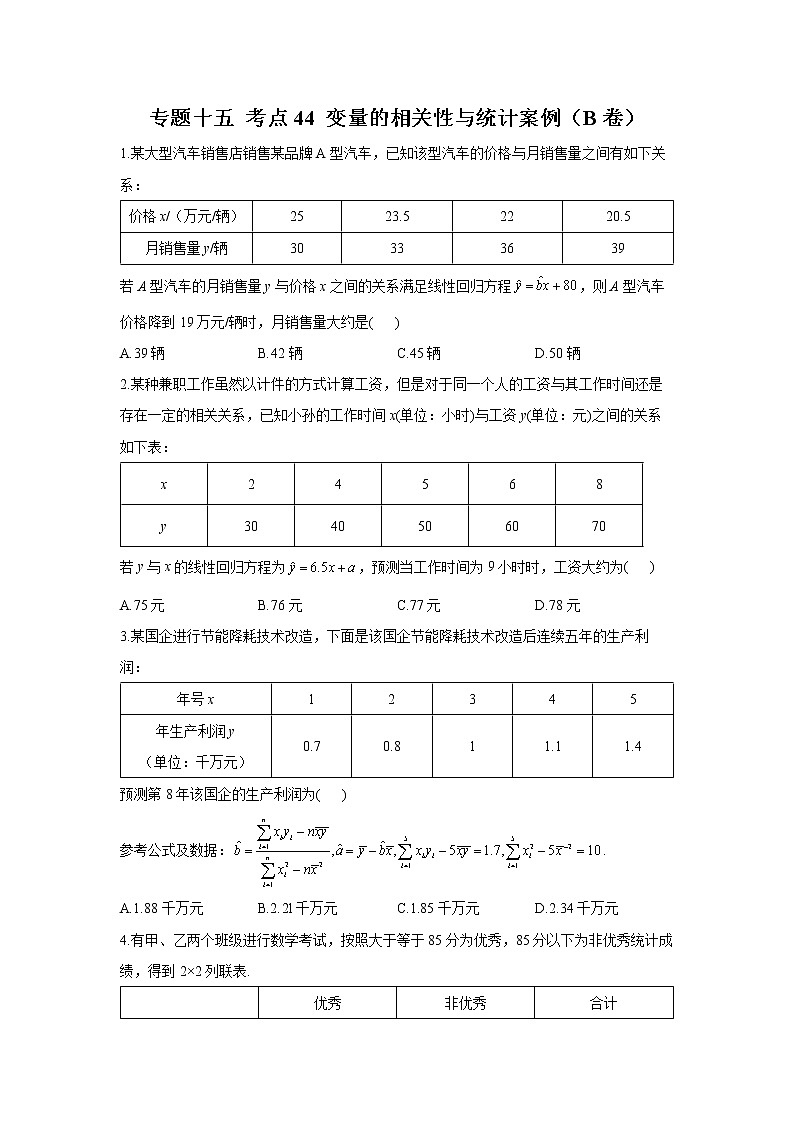
专题十五 考点44 变量的相关性与统计案例(B卷)
1.某大型汽车销售店销售某品牌A型汽车,已知该型汽车的价格与月销售量之间有如下关系:
价格x/(万元/辆) | 25 | 23.5 | 22 | 20.5 |
月销售量y/辆 | 30 | 33 | 36 | 39 |
若A型汽车的月销售量y与价格x之间的关系满足线性回归方程,则A型汽车价格降到19万元/辆时,月销售量大约是( )
A.39辆 B.42辆 C.45辆 D.50辆
2.某种兼职工作虽然以计件的方式计算工资,但是对于同一个人的工资与其工作时间还是存在一定的相关关系,已知小孙的工作时间x(单位:小时)与工资y(单位:元)之间的关系如下表:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 50 | 60 | 70 |
若y与x的线性回归方程为,预测当工作时间为9小时时,工资大约为( )
A.75元 B.76元 C.77元 D.78元
3.某国企进行节能降耗技术改造,下面是该国企节能降耗技术改造后连续五年的生产利润:
年号x | 1 | 2 | 3 | 4 | 5 |
年生产利润y (单位:千万元) | 0.7 | 0.8 | 1 | 1.1 | 1.4 |
预测第8年该国企的生产利润为( )
参考公式及数据:.
A.1.88千万元 B.2.2l千万元 C.1.85千万元 D.2.34千万元
4.有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到2×2列联表.
| 优秀 | 非优秀 | 合计 |
甲班 | 10 | b |
|
乙班 | c | 30 |
|
合计 |
|
| 105 |
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法正确的是( )
参考公式:
附表:
0.050 | 0.010 | 0.001 | |
k | 3.841 | 6.635 | 10.828 |
A.列联表中c的值为30,b的值为35
B.列联表中c的值为15,b的值为50
C.根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”
D.根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”
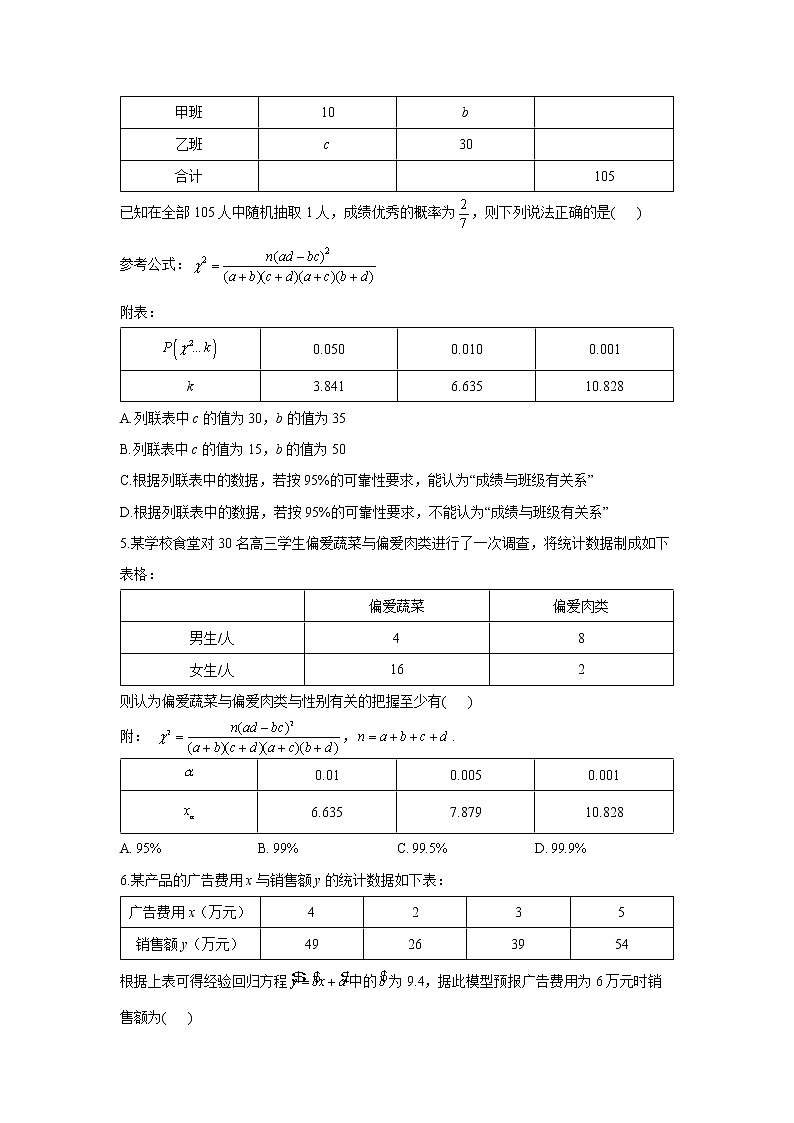
5.某学校食堂对30名高三学生偏爱蔬菜与偏爱肉类进行了一次调查,将统计数据制成如下表格:
| 偏爱蔬菜 | 偏爱肉类 |
男生/人 | 4 | 8 |
女生/人 | 16 | 2 |
则认为偏爱蔬菜与偏爱肉类与性别有关的把握至少有( )
附: ,.
0.01 | 0.005 | 0.001 | |
6.635 | 7.879 | 10.828 |
A. B. C. D.
6.某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得经验回归方程中的为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
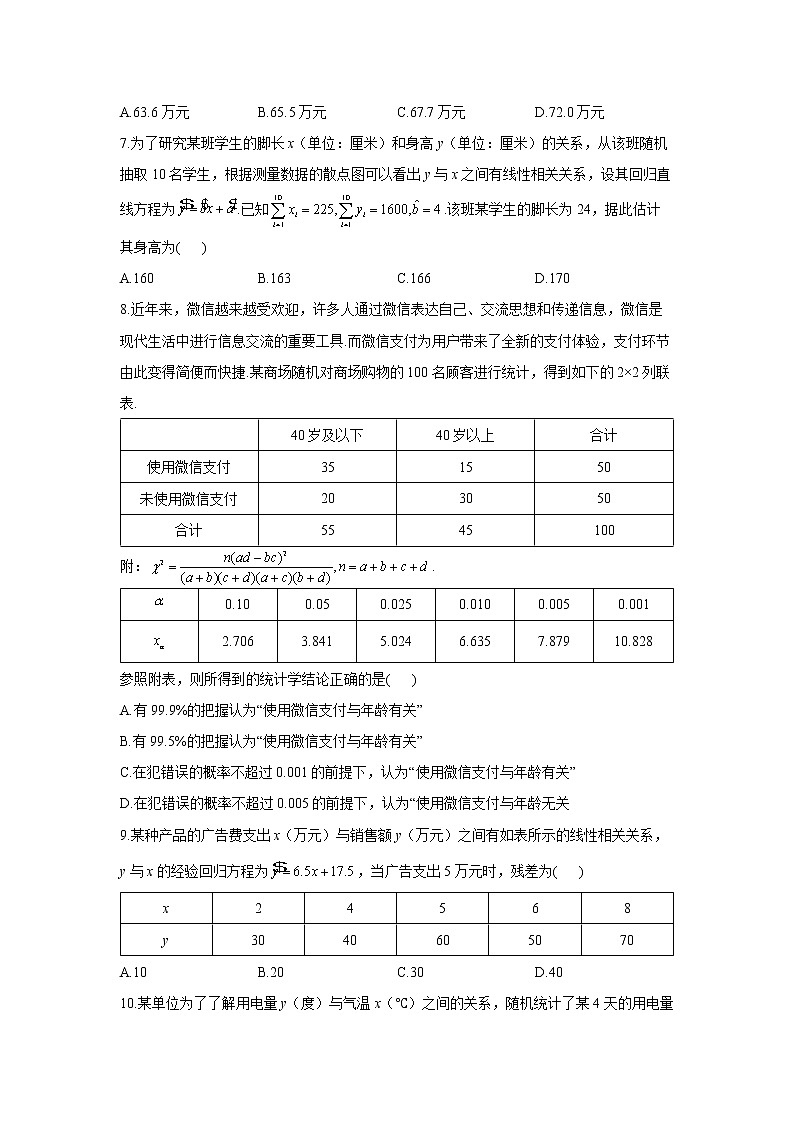
7.为了研究某班学生的脚长x(单位:厘米)和身高y(单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y与x之间有线性相关关系,设其回归直线方程为.已知.该班某学生的脚长为24,据此估计其身高为( )
A.160 B.163 C.166 D.170
8.近年来,微信越来越受欢迎,许多人通过微信表达自己、交流思想和传递信息,微信是现代生活中进行信息交流的重要工具.而微信支付为用户带来了全新的支付体验,支付环节由此变得简便而快捷.某商场随机对商场购物的100名顾客进行统计,得到如下的2×2列联表.
| 40岁及以下 | 40岁以上 | 合计 |
使用微信支付 | 35 | 15 | 50 |
未使用微信支付 | 20 | 30 | 50 |
合计 | 55 | 45 | 100 |
附:.
0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参照附表,则所得到的统计学结论正确的是( )
A.有99.9%的把握认为“使用微信支付与年龄有关”
B.有99.5%的把握认为“使用微信支付与年龄有关”
C.在犯错误的概率不超过0.001的前提下,认为“使用微信支付与年龄有关”
D.在犯错误的概率不超过0.005的前提下,认为“使用微信支付与年龄无关
9.某种产品的广告费支出x(万元)与销售额y(万元)之间有如表所示的线性相关关系,y与x的经验回归方程为,当广告支出5万元时,残差为( )
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
A.10 B.20 C.30 D.40
10.某单位为了了解用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了如下对照表,由表中数据得经验回归方程,其中.现预测当气温为-4℃时,用电量的度数为____________.
气温x(℃) | 18 | 13 | 10 | -1 |
用电量y(度) | 24 | 34 | 38 | 64 |
11.某部门通过随机调查89名工作人员的休闲方式是读书还是健身,得到的数据如下表:
单位:人
| 读书 | 健身 | 合计 |
女 | 24 | 31 | 55 |
男 | 8 | 26 | 34 |
合计 | 32 | 57 | 89 |
在犯错误的概率不超过__________的前提下认为性别与休闲方式有关系.
附表:
0.1 | 0.05 | 0.01 | 0.005 | 0.001 | |
2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
12.某工厂为研究某种产品产量(吨)与所需某种原材料(吨)的相关性,在生产过程中收集4组对应数据如表所示:(残差=真实值预测值)
3 | 4 | 5 | 6 | |
2.5 | 3 | 4 |
根据表中数据,得出关于的线性回归方程为.据此计算出在样本点处的残差为,则表中的值为______________.
13.已知某班学生每周用于物理学习的时间x(单位:h)与物理成绩y(单位:分)的几组数据如下:
x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
根据上表可得回归直线的斜率为3.53,则回归直线在y轴上的截距为___________(结果保留到0.1).
14.2021年5月22日10时40分,“祝融号”火星车已安全驶离着陆平台,到达火星表面,开始巡视探测.为了增强学生的科技意识,某学校进行了一次专题讲座,讲座结束后,进行了一次专题测试(满分:100分),其中理科学生有600名学生参与测试,其得分都在内,得分情况绘制成频率分布直方图如下,在区间的频率依次构成等差数列.
若规定得分不低于80分者为优秀,文科生有400名学生参与测试,其中得分优秀的学生有50名.
(1)若以每组数据的中间值代替本组数据,求理科学生得分的平均值;
(2)请根据所给数据完成下面的列联表,并说明是否有99.9%以上的把握认为,得分是否优秀与文理科有关?
| 优秀 | 不优秀 | 合计 |
理科生 |
|
|
|
文科生 |
|
|
|
合计 |
|
| 1000 |
附:,其中.
0.050 | 0.010 | 0.001 | |
3.841 | 6.635 | 10.828 |
15.某物流公司运用新技术进行公司管理.为了解其管辖的收发部的经营状况,运用大数据技术随机记录了该部开业后第1~5月的月营业额y(单位:万元)与月份x的数据,如表:
x | 1 | 2 | 3 | 4 | 5 |
y | 10 | 12 | 15 | 14 | 19 |
(1)求y关于x的回归直线方程;
(2)若在这些样本点中任取两点,求恰有一点在回归直线上的概率.
附:回归直线方程中,,.
答案以及解析
1.答案:B
解析:由表中数据可求得,,代入线性回归方程,得,所以.将代入线性回归方程,得,即月销售量大约为42辆.
2.答案:B
解析:由表格数据知:,,
,线性回归方程为,
,即当工作时间为9小时时,工资大约为76元.
故选:B.
3.答案:C
解析:由题可得,所以,所以年生产利润关于年号的经验回归方程为,
当时,,故选C.
4.答案:C
解析:由题意知,成绩优秀的学生数是,成绩非优秀的学生数是,所以,则选项A,B错误;根据列联表中的数据,得到,因此有95%的把握认为“成绩与班级有关系”,则选项C正确.故选C.
5.答案:C
解析:由已知,列联表为
| 偏爱蔬菜 | 偏爱肉类 | 合计 |
男生/人 | 4 | 8 | 12 |
女生/人 | 16 | 2 | 18 |
合计 | 20 | 10 | 30 |
则,
故至少有的把握认为偏爱蔬菜与偏爱肉类与性别有关,故选C.
6.答案:B
解析:.
数据样本点的中心在经验回归直线上,经验回归方程中的为9.4,,解得.
经验回归方程是.
广告费用为6万元时销售额的预测值为(万元),故选B.
7.答案:C
解析:.
又中,回归直线一定过样本点的中心,
.
当时,.故选C.
8.答案:B
解析:由列联表中的数据计算,所以有99.5%的把握认为“使用微信支付与年龄有关”.故选B.
9.答案:A
解析:因为y与x的经验回归方程为,
所以当时,.
由表格知当广告支出5万元时,销售额为60万元,所以残差为.故选A.
10.答案:68
解析:由题表中数据可得,,所以经验回归直线过点,故.
所以当时,.
11.答案:0.1
解析:由题中列联表中的数据,得,因为,所以在犯错误的概率不超过0.1的前提下认为性别与休闲方式有关系 .
12.答案:4.5
解析:由在样本点处的残差为,可得,则,解得,由题意可知,产量的平均数为,由线性回归方程过点,则,则,解得.
13.答案:13.5
解析:由已知可得,.
设回归直线方程为,则,解得,所以回归直线在y轴上的截距为13.5.
14.答案:(1)理科学生得分的平均值为73分.
(2)表格见解析,有99.9%以上的把握认为得分是否优秀与文理科有关.
解析:(1)由第三、二、四组的频率依次构成等差数列可得.
又频率分布直方图中所有小矩形面积之和为1,则,
解得,
理科学生得分的平均值为(分).
(2)理科学生优秀的人数为,
补全2×2列联表如表所示,
| 优秀 | 不优秀 | 合计 |
理科生 | 150 | 450 | 600 |
文科生 | 50 | 350 | 400 |
合计 | 200 | 800 | 1000 |
,
有99.9%以上的把握认为得分是否优秀与文理科有关.
15.答案:(1)
(2)
解析:(1)根据表中数据得,,,
,,
所以,
于是,
所以y关于x的回归直线方程为.
(2)用m,n分别表示所取的两个样本点所在的月份,
则该试验的基本事件可以表示为实数组,
于是该试验的基本事件空间
,
共10个基本事件.
当或,即m,n取1或2时,点在回归直线上.
设“恰有一点在回归直线上”为事件A,
则中,
共6个满足条件的事件,
所以.
相关试卷
这是一份2023届高考数学二轮复习专题专题十八变量的相关性与统计案例作业(B)含答案,共14页。
这是一份2023年高考数学二轮复习重点基础练习:专题十五 统计与统计案例 综合练习(B卷),共10页。试卷主要包含了4%等内容,欢迎下载使用。
这是一份2023年高考数学二轮复习重点基础练习:专题十五 统计与统计案例 综合练习(A卷),共10页。试卷主要包含了25次,5次,5万元B等内容,欢迎下载使用。












