2023年高考数学二轮复习重点基础练习：专题十五 考点43 随机抽样与用样本估计总体（A卷）

专题十五 考点43 随机抽样与用样本估计总体（A卷）

1.已知样本数据2，4，6，a的平均数为4，则该样本的标准差是(   )
A. B. C.2 D.

2.某小区居民上网年龄分布图如图所示，现按照分层抽样的方法从该小区抽取一个容量为n的样本.若90后比00后多52人，则(   )

A.450 B.400 C.550 D.500

3.某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果，随机抽取10位社区居民，让他们在讲座前和讲座后各回答一份垃圾分类知识问卷，这10位社区居民在讲座前和讲座后问卷答题的正确率如图，则(   )

A.讲座前问卷答题的正确率的中位数小于70%

B.讲座后问卷答题的正确率的平均数大于85%

C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差

D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差

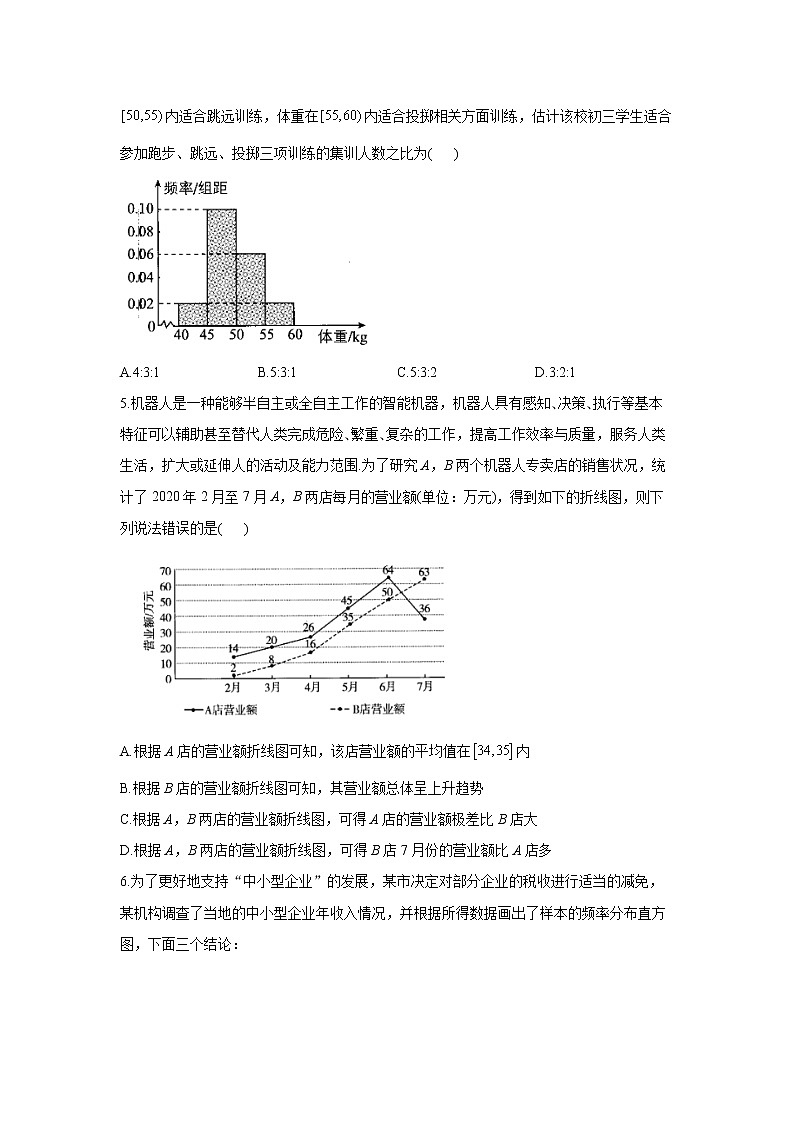
4.某校为了对初三学生的体重进行摸底调查，随机抽取了50名学生的体重（kg），将所得数据整理后，画出了频率分布直方图.如图所示，体重在内适合跑步训练，体重在内适合跳远训练，体重在内适合投掷相关方面训练，估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为(   )

A.4:3:1 B.5:3:1 C.5:3:2 D.3:2:1

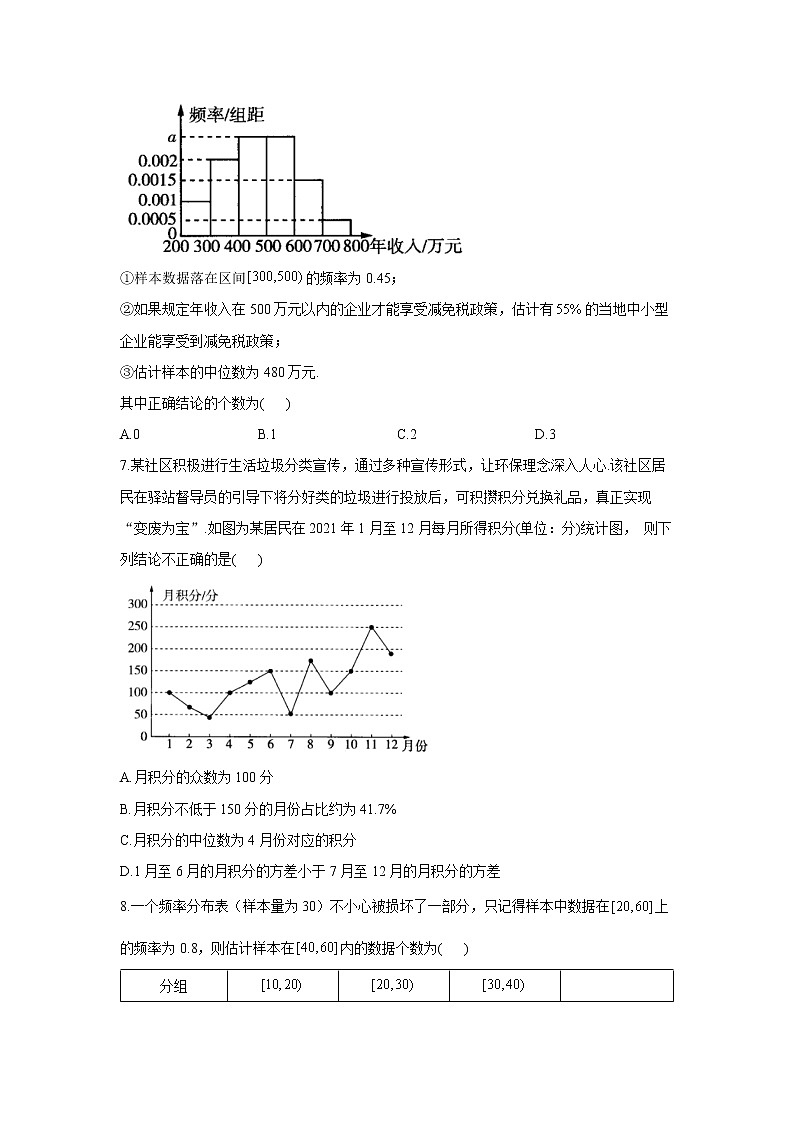
5.机器人是一种能够半自主或全自主工作的智能机器，机器人具有感知､决策､执行等基本特征可以辅助甚至替代人类完成危险､繁重､复杂的工作，提高工作效率与质量，服务人类生活，扩大或延伸人的活动及能力范围.为了研究A，B两个机器人专卖店的销售状况，统计了2020年2月至7月A，B两店每月的营业额(单位：万元)，得到如下的折线图，则下列说法错误的是(   )

A.根据A店的营业额折线图可知，该店营业额的平均值在内

B.根据B店的营业额折线图可知，其营业额总体呈上升趋势

C.根据A，B两店的营业额折线图，可得A店的营业额极差比B店大

D.根据A，B两店的营业额折线图，可得B店7月份的营业额比A店多

6.为了更好地支持“中小型企业”的发展，某市决定对部分企业的税收进行适当的减免，某机构调查了当地的中小型企业年收入情况，并根据所得数据画出了样本的频率分布直方图，下面三个结论：

①样本数据落在区间的频率为0.45；
②如果规定年收入在500万元以内的企业才能享受减免税政策，估计有的当地中小型企业能享受到减免税政策；
③估计样本的中位数为480万元.
其中正确结论的个数为(   )

A.0 B.1 C.2 D.3

7.某社区积极进行生活垃圾分类宣传，通过多种宣传形式，让环保理念深入人心.该社区居民在驿站督导员的引导下将分好类的垃圾进行投放后，可积攒积分兑换礼品，真正实现“变废为宝”.如图为某居民在2021年1月至12月每月所得积分(单位：分)统计图， 则下列结论不正确的是(   )

A.月积分的众数为100分

B.月积分不低于150分的月份占比约为41.7%

C.月积分的中位数为4月份对应的积分

D.1月至6月的月积分的方差小于7月至12月的月积分的方差

8.一个频率分布表（样本量为30）不小心被损坏了一部分，只记得样本中数据在上的频率为0.8，则估计样本在内的数据个数为(   )

A.14 B.15 C.16 D.17

9.对“小康县”的经济评价标准：①年人均收入不低于7000元；②年人均食品支出不高于年人均收入的35%.某县有40万人，年人均收入如下表所示，年人均食品支出如图所示，则该县(   )

A.是小康县

B.达到标准①，未达到标准②，不是小康县

C.达到标准②，未达到标准①，不是小康县

D.两个标准都未达到，不是小康县

10.某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200，400，300，100件，为检验产品的质量，现用分层随机抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取_____件.

11.随着社会的发展，食品安全问题渐渐成为社会关注的热点，为了提高学生的食品安全意识，某学校组织全校学生参加食品安全知识竞赛，成绩的频率分布直方图如图所示，数据的分组依次为，若该校的学生总人数为3000，则成绩不超过60分的学生人数大约为_________.

12.某医院急救中心随机抽取20位病人等待急诊的时间（单位：分）记录如下表：

用上述分组资料计算出病人平均等待时间的估计值_________，病人等待时间方差的估计值________.

13.如图（1）是根据某中学为地震灾区捐款的情况而制作的统计图.已知该校在校学生有3000人，结合统计图（2）计算该校共捐款___________元.

14.M公司从某大学招收毕业生，经过综合测试，录用了14名男生和6名女生，这20名毕业生的测试成绩（单位：分）如下：

男：165 166 168 172 173 174 175

176 177 182 184 185 193 194

女：168 177 178 185 186 192

公司规定：成绩在180分以上（包括180分）者到“甲部门”工作；180分以下者到“乙部门”工作.

（1）求男生成绩的中位数及女生成绩的平均数.

（2）如果用分层随机抽样的方法从“甲部门”人选和“乙部门”人选中共选取5人，再从这5人中选2人，那么至少有一人是“甲部门”人选的概率是多少？

15.某校从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：，，…，后得到如图所示的频率分布直方图.

（1）求图中实数a的值；

（2）若该校高一年级共有学生640人，试估计该校高一年级期中考试数学成绩不低于60分的人数；

（3）若从数学成绩在与两个分数段内的学生中随机选取2名学生，求这2名学生的数学成绩之差的绝对值不大于10的概率.

答案以及解析

1.答案：B

解析：因为2，4，6，a的平均数为4，所以，得，所以该样本的标准差，故选B.

2.答案：B

解析：根据题意可知，解得，故选B.

3.答案：B

解析：对于A，讲座前问卷答题的正确率的中位数是，所以A错误；对于B，讲座后问卷答题的正确率分别是80%，85%，85%，85%，85%，90%，90%，95%，100%，100%，其平均数显然大于85%，所以B正确；对于C，由题图可知，讲座前问卷答题的正确率波动较大，讲座后问卷答题的正确率波动较小，所以讲座前问卷答题的正确率的标准差大于讲座后问卷答题的正确率的标准差，所以C错误；对于D，讲座前问卷答题的正确率的极差是，讲座后问卷答题的正确率的极差是，所以讲座前问卷答题的正确率的极差大于讲座后问卷答题的正确率的极差，所以D错误.故选B.

4.答案：B

解析：体重在内的频率为，体重在内的频率为，体重在内的频率为，

，

可估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为5:3:1.故选B.

5.答案：C

解析：根据A店的营业额折线图可知，该店营业额的平均值为：，故A正确；

根据B店的营业额折线图可知，其营业额总体呈上升趋势，故B正确；

A店的营业额的极差为：，B店的营业额的极差为，故A店的营业额极差比B店小，故C错误；

由折线图可知B店7月份的营业额比A店多，故D正确.

故选：C.

6.答案：D

解析：由，得，
所以数据在区间的频率为，①正确；
数据在区间的频率为，②正确；
数据在区间的频率为0.3，数据在区间的频率为0.55，
故估计中位数为，③正确.

7.答案：C

解析：A.由题图易知月积分的众数为100分， 故A正确;

B.月积分不低于150 分的月份有5 个，，故所求月份占比约为41.7%，故 B正确；

C.月积分的中位数大于100分，不是4月份对应的积分，故C不正确

D.1月至6月的月积分变化相对于7月至12月的月积分变化波动较小，所以方差也较小，故D正确.

8.答案：B

解析：一个频率分布表（样本量为30）不小心被损坏了一部分，只记得样本中数据在上的频率为0.8，

样本中数据在上的频数为，

估计样本在内的数据个数为.故选B.

9.答案：B

解析：由题中图表可知，年人均收入为(元)，达到了标准①；年人均食品支出为(元)，则年人均食品支出占年人均收入的，未达到标准②.所以不是小康县.

10.答案：18

解析：应从丙种型号的产品中抽取(件).

11.答案：900

解析：由频率分布直方图知，成绩不超过60分的学生的频率为，

所以成绩不超过60分的学生人数大约为.

12.答案：9.5；28.5

解析：，.

13.答案：37 770

解析：根据统计图，得

高一人数为，捐款元；

高二人数为，捐款元；

高三人数为，捐款元.

所以该校学生共捐款元.

14.答案：（1）男生成绩的中位数是175.5，女生成绩的平均数是181

（2）

解析：（1）男生共有14人，将男生成绩按从小到大的顺序排列，中间两个成绩是175和176，因此男生成绩的中位数是175.5.

女生成绩的平均数.

（2）用分层随机抽样的方法从“甲部门”人选和“乙部门”人选共20人中轴取5人，每个人被抽中的概率是.

由题意可知，“甲部门”人选有8人，“乙部门”人选有12人.

所以选取的“甲部门”的人选有（人），

“乙部门”的人选有（人）.

记选中的“甲部门”的人选为，，选中的“乙部门”的人选为B，C，D.从这5人中选2人的所有可能结果为，，，，，，，，，，共10种.

其中至少有一人是“甲部门”人选的结果有7种.

因此，至少有一人是“甲部门”人选的概率是.

15.答案：（1）

（2）544

（3）

解析：（1）由已知，得，解得.

（2）根据频率分布直方图，可知成绩不低于60分的频率为.由于该校高一年级共有学生640人，利用样本估计总体的思想，可估计该校高一年级期中考试数学成绩不低于60分的人数为.

（3）易知成绩在分数段内的人数为，这2人分别记为A，B；成绩在分数段内的人数为，这4人分别记为C，D，E，F.若从数学成绩在与两个分数段内的学生中随机选取2名学生，则样本空间，共15个样本点.如果2名学生的数学成绩都在分数段内或都在分数段内，那么这2名学生的数学成绩之差的绝对值一定不大于10.如果一个成绩在分数段内，另一个成绩在分数段内，那么这2名学生的数学成绩之差的绝对值一定大于10.记“这2名学生的数学成绩之差的绝对值不大于10”为事件M，则，共7个样本点.故所求概率.