








湘教版八年级下册第3章 图形与坐标3.3 轴对称和平移的坐标表示优质课课件ppt
展开第3章 图形与坐标
3.3 轴对称和平移的坐标表示
第2课时 平移的坐标表示
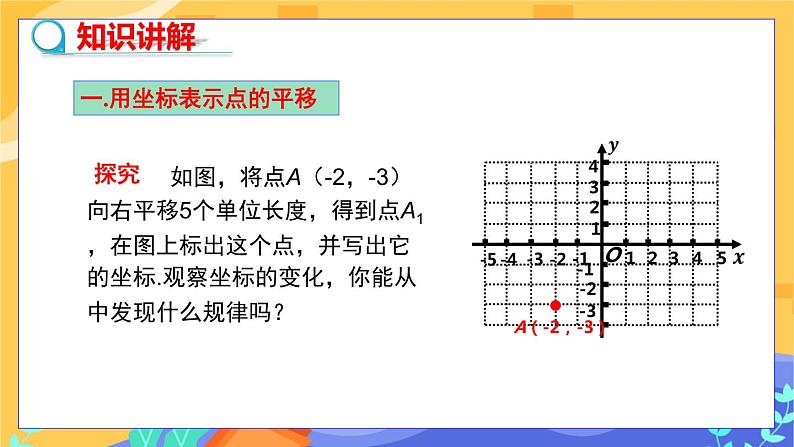
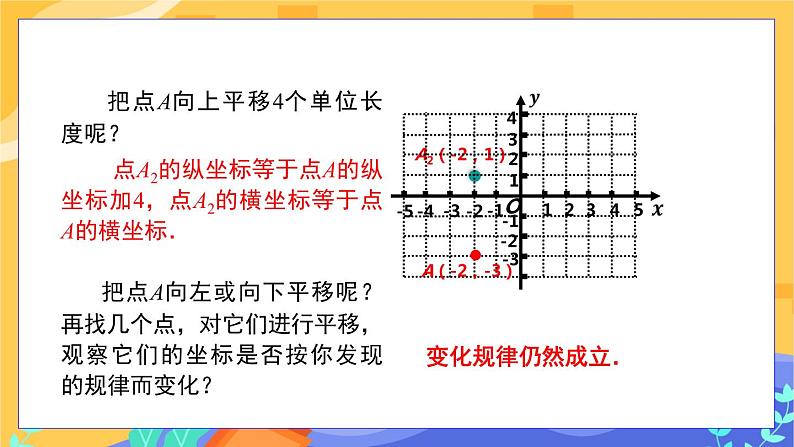
教学目标 1.掌握图形在平面直角坐标系中平移前后点的坐标的变化规律. 2.用点的坐标变化表示图形的平移. 3.体会平面直角坐标系是数与形之间的桥梁,感受代数与几何的相互转化,初步建立空间概念. 教学重难点 重点:探究平面直角坐标系中平移前后点的坐标的变化规律. 难点:平移前后点的坐标的变化规律的应用, 教学过程 导入新课 教师:如图1,数轴上点表示的数是 ,点A 向右平移两个单位后表示的数是 .点B表示的数是 ,点B向左平移3个单位后表示的数是 . 从数轴上的点的平移你发现了什么?说出来与大家分享你的重大发现. 图1 学生回答上面的横线问题,并讨论点的平移变化规律 教师引导得出结论:点的移动变化规律是左加右减. 探究新知 探究点一:点的左右平移与坐标的变化规律 教师:(1)请同学们准备好坐标纸,并在坐标纸上建立平面直角坐标系,描出点A(-2,-3).将点A向右平移5个单位长度得到点,在图2上标出这个点,并写出它的坐标. (2)将点A(-2,-3)向右平移4个单位长度,得到点,在图2上标出这个点,并写出它的坐标. (3)你能说出上述两种平移变化后,坐标的变化规律吗? 图2 师生活动 同学们拿出已准备好的坐标纸,建立平面直角坐标系,在坐标系中画出相应的点,教师在学生回答的基础上,进一步补充、完善,得出结论.将点A(-2,-3)向右平移5个单位长度,得到的新坐标是:纵坐标不变,横坐标加5.将点A(-2,-3)向右平移4个单位长度,得到的新坐标是:纵坐标不变,横坐标加4.可得A1 (3,-3),A2 (2,-3). 教师:若将点A(-2,-3)向右平移a(a>0)个单位长度,得到的点的坐标是什么?这个点向右平移后,点的横纵坐标发生了什么变化? 学生回答,最后教师归纳:点向右平移时,纵坐标不变,横坐标增大. 在活动中教师应重点关注:点的坐标描得是否准确;学生能否在独立思考的基础上,积极参与对数学问题的讨论,并能发表自己的见解;运用数学语言表述问题的能力. 教师:在平面直角坐标系中将点B(-2,4)向左平移3个单位长度,写出它的坐标;如果将点B(-2,4)向左平移4个单位长度,写出它的坐标,并分析它们的坐标变化规律. 学生回答,如有不足,其他同学补充,最后教师归纳:在点B向左平移时,纵坐标不变,横坐标减3或减4. 教师:若将点B(-2,4)向左移动a(a>0)个单位长度,它的坐标是什么?这个点向左平移时,点的横纵坐标发生了什么变化? 学生回答,如有不足,教师补充,最后教师总结:当一个点向左平移时,纵坐标不变,横坐标减小. 教师:思考如果原图形上的点是(x,y),向右平移a(a>0)个单位长度,新点的坐标应怎样表示? 学生回答,教师板书(如图3所示).教师给予肯定和表扬. 教师追问,如果点(x,y)向左平移呢? 学生回答,教师板书(如图3所示). 探究点二:点的上下平移与坐标的变化规律 教师:刚刚我们研究了点左右平移时点的坐标的变化规律,现在我们研究点上下平移时,点的坐标有什么样的变化,出示问题:在坐标纸上标出点C(3,-1)的位置,然后按照下列提示平移,观察平移后点的坐标变化规律. ①点C(3,-1)向上平移3个单位长度得到C1, ②点C(3,-1)向上平移5个单位长度得到C2, ③点C(3,-1)向下平移3个单位长度得到C3, ④点C(3,-1)向下平移5个单位长度得到C4. 学生在坐标纸上标出C1,C2,C3,C4四个点并写出它们的坐标,然后展示.教师追问:点C在向上平移时得到点C1,C2,它们的坐标是怎样变化的?点C在向下平移时得到点C3,C4,它们的坐标是怎样变化的? 学生回答,如有不足,其他同学补充. 教师:如果点C(3,-1)改为点(x,y)向上或下平移b个单位长度,它们的坐标分别是什么? 学生回答,如有不足,其他同学补充,最后教师总结并板书(如图3所示). 图3 即左右平移→左减右加纵不变;上下平移→上加下减横不变 新知应用 例1 平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( ) A.(1,-8) B.(1,-2) C.(-6,-1) D.(0,-1) 解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1). 答案:C 探究点三:图形左右平移时点的坐标变化 如图4,△ABC 在坐标平面内平移后得到新图形△A1B1C1. 图4 问题: (1)移动的方向怎样? (2)写出△ABC与△A1B1C1各顶点坐标.比较对应点的坐标,看有怎样的变化?学生讨论进行回答. 解:(1)向左平移了5个单位. (2) 教师:如果把△ABC向右平移2个单位,得到△A2B2C2. 写出这时各顶点坐标,比较两者对应点坐标,看有怎样的变化. 学生讨论进行回答 总结与归纳:观察上面数据,你发现了什么?把平面直角坐标系中的一个图形,向左或向右移动(>0)个单位,那么图形上任何一个点的坐标()是如何变化的? 学生:把平面直角坐标系中的一个图形,向左或向右移动(>0)个单位,那么图形上任何一个点的坐标变化是一样的,即 探究点四:图形上下平移时点的坐标变化 教师:如图5,△ ABC向下平移2个单位,得到△A1B1C1. 图5 写出这时各顶点坐标,比较两者对应点坐标,看有怎样的变化. 学生进行回答. 各顶点坐标的变化情况: 教师:如果△ABC向上平移1个单位,得到△A2B2C2. 图6 写出这时各顶点坐标,比较两者对应点坐标,看有怎样的变化. 学生进行回答.各顶点坐标的变化情况: 总结与归纳:观察上面数据,你发现了什么? 学生:把平面直角坐标系中的一个图形,向上或向下移动(>0)个单位,那么图形上任何一个点的坐标变化是一样的,即 教师:把平面直角坐标系中的一个图形,向左或向右移动个单位,再向上或向下移动个单位,那么图形上任何一个点的坐标()是如何变化的? 师生活动 学生思考、讨论后回答, 例2 如图7,△ ABC的三个顶点坐标分别为A(3,3),B(2,1),C(5,1). 图7 (1)将△ABC向下平移5个单位,作出它的图象,并写出它的顶点坐标; (2)将△ABC向左平移7个单位,作出它的图象,并写出它的顶点坐标. 分析:根据平移的性质,将△ABC向下或向左平移k个单位,△ABC的每一个顶点都向下或向左平移了k个单位,求出顶点A,B,C的坐标,作出这些像点,依次连接它们,即可得到△ABC的图象. 解:(1)将△ABC向下平移5个单位,则横坐标不变,纵坐标减5,由点A,B,C的坐标可知A1(3,-2),B1(2,-4),C1(5,-4),依次连接点A1,B1,C1,即可得△A1B1C1,如图8. (2)将△ABC向左平移7个单位,则横坐标减7,纵坐标不变,由点A,B,C的坐标可知A2(-4,3),B2(-5,1),C2(-2,1),依次连接点A2,B2,C2,即可得△A2B2C2,如图8. 图8 教师:一个图形依次沿两个坐标轴方向平移所得到的图形,还可以怎样得到? 师生共同归纳:一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到. 总结:对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
课堂小结 教师和学生一起回顾本节课所学内容,并请学生回答以下问题: 1.点沿坐标轴方向平移后坐标的变化规律是什么? 2.将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形做一次平移得到吗?请举例说明. 师生活动 学生归纳总结,教师补充升华. 布置作业 教材第102页习题3.3第3,4,5题 板书设计 3.3 轴对称和平移的坐标表示 第2课时 平移的坐标表示 1. 1. 2.对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移. |
初中数学湘教版八年级下册3.3 轴对称和平移的坐标表示精品课件ppt: 这是一份初中数学湘教版八年级下册3.3 轴对称和平移的坐标表示精品课件ppt,文件包含第2课时简单平移的坐标表示课件pptx、第1课时轴对称的坐标表示课件pptx、第3课时综合平移的坐标表示课件pptx、33轴对称和平移的坐标表示练习pptx、第1课时轴对称的坐标表示教案doc、第2课时简单平移的坐标表示教案doc、第3课时综合平移的坐标表示教案doc等7份课件配套教学资源,其中PPT共71页, 欢迎下载使用。
初中数学湘教版八年级下册3.3 轴对称和平移的坐标表示优秀ppt课件: 这是一份初中数学湘教版八年级下册3.3 轴对称和平移的坐标表示优秀ppt课件,文件包含第2课时简单平移的坐标表示课件pptx、第1课时轴对称的坐标表示课件pptx、第3课时综合平移的坐标表示课件pptx、33轴对称和平移的坐标表示练习pptx、第1课时轴对称的坐标表示教案doc、第2课时简单平移的坐标表示教案doc、第3课时综合平移的坐标表示教案doc等7份课件配套教学资源,其中PPT共71页, 欢迎下载使用。
湘教版八年级下册3.3 轴对称和平移的坐标表示优秀ppt课件: 这是一份湘教版八年级下册3.3 轴对称和平移的坐标表示优秀ppt课件,文件包含教学课件八下·湘教·33轴对称和平移的坐标表示第1课时轴对称的坐标表示pptx、33轴对称和平移的坐标表示第1课时教案docx、33轴对称和平移的坐标表示第1课时同步练习docx等3份课件配套教学资源,其中PPT共22页, 欢迎下载使用。














