初中数学湘教版八年级下册第1章 直角三角形1.1 直角三角形的性质与判定（Ⅰ）精品课件ppt

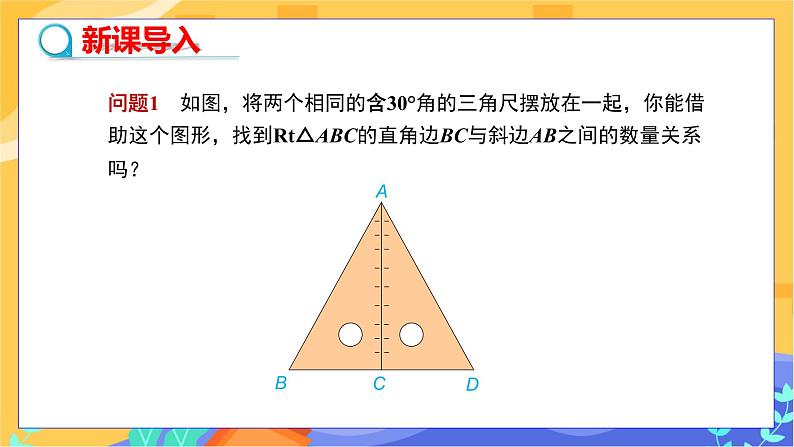
教学目标

1.理解和掌握有关30°角的直角三角形的性质和应用;

2.通过定理的证明和应用，初步了解转化思想，并培养分析问题和解决问题的能力．

教学重难点

重点：直角三角形的性质及推论的理解与应用.

难点：对“在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半”的图形结合的理解.

教学过程

导入新课

问题1 如图12，将两个相同的含30°角的三角尺摆放在一起，你能借助这个图形，找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗？

图12

问题2 将一张等边三角形纸片，沿一边上的高对折，你有什么发现？

图13

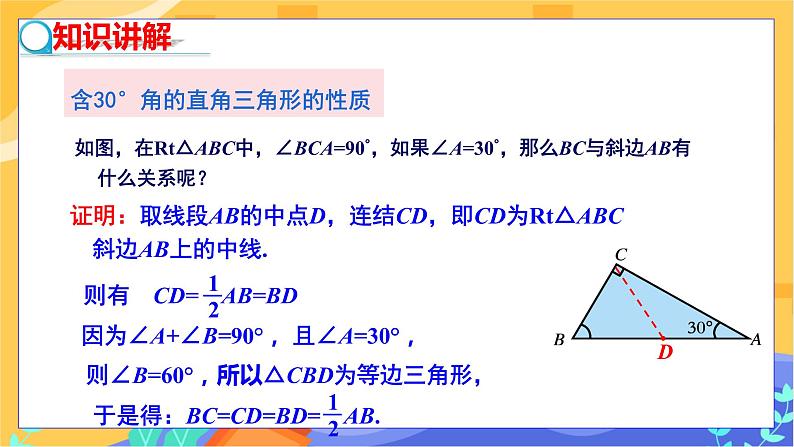
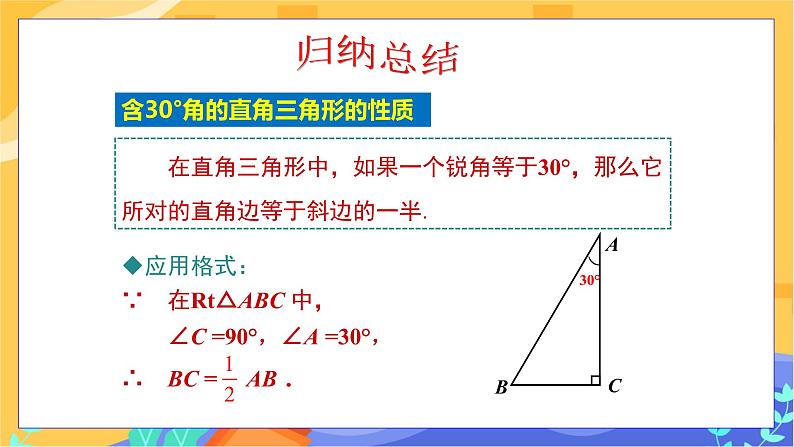
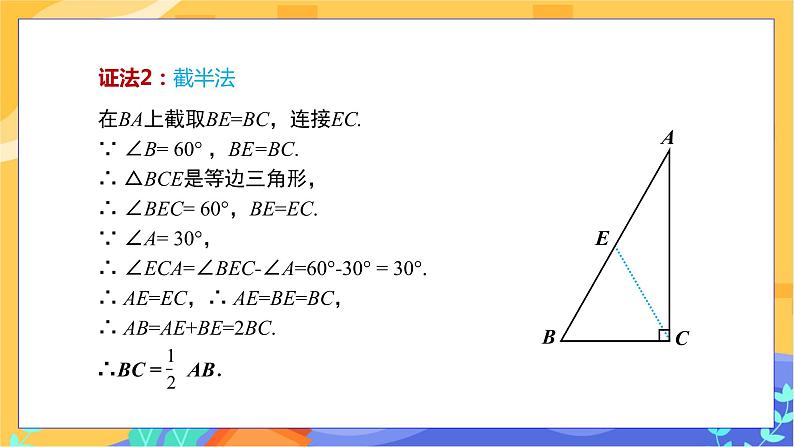
探究新知

【探究1】含30°角的直角三角形的性质

在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．

应用格式：

∵ 在Rt△ABC 中，∠C ＝90°，∠A＝30°，　

∴ BC＝AB.

图14

思考：在Rt△ABC中，∠BCA＝90°，如果∠A＝30°，那么直角边BC与斜边AB有什么关系？

(学生利用几何工具，先画出图形，然后再测量，得出答案)

结论：BC＝ AB.

学生利用前面学过的直角三角形斜边上的中线等于斜边的一半和等腰三角形、等边三角形的性质综合分析．

证明：如图15取线段AB的中点D，连结CD，即CD为Rt△ABC斜边AB上的中线，则有CD＝AB＝BD.

因为∠ A+∠ B＝90°，且∠ A＝30°，则∠ B＝60°，

所以△CBD为等边三角形，

于是得：BC＝CD＝BD＝AB.

图15

(鼓励学生思考：这个定理的得出除了上面的方法外，你还有没有别的方法呢？引导学生积极思考)

证法1：倍长法

已知：如图16，在Rt△ABC中，∠C＝90°，∠A＝30°.

求证：BC＝AB.

证明：在△ABC中，∵ ∠ACB＝90°，∠BAC＝30°，∴ ∠B＝60°.

延长BC到D，使BD＝AB，连接AD，则△ABD是等边三角形.

又∵ AC⊥BD，∴ BC＝BD.

∴ BC＝AB.

图16

证法2：截半法

如图17，在BA上截取BE＝BC，连接EC.

∵ ∠B＝60°，BE＝BC.

∴ △BCE是等边三角形，

∴ ∠BEC＝60°，BE＝EC.

∵ ∠A＝30°，

∴ ∠ECA＝∠BEC-∠A＝60°-30°＝30°.

∴ AE＝EC，∴ AE＝BE＝BC，

∴ AB＝AE+BE＝2BC.

∴ BC＝AB.

图17

【探究2】：上述命题中，把条件“∠A＝30°”与结论“BC＝ AB” 交

换，命题还成立吗？

引导学生发现，在直角三角形中，一个角等于30°与30°角所对的直角边等于斜边的一半在命题中相互调换，结论都成立．

应用格式：

∵ 在Rt△ ABC中，∠ C＝90°，BC＝AB，

∴ ∠A＝30°.

图18

通过对比，认清了它们之间的区别与联系.

新知应用

例1 如图19，在Rt△ABC中，∠ACB＝90°，∠B＝30°，CD是斜边AB上的高，AD＝3 cm，则AB的长度是(　　)

    A．3 cm            B．6 cm           C．9 cm          D．12 cm

图19

解析：在Rt△ABC中，∵ CD是斜边AB上的高，

∴ ∠ADC＝90°，∴ ∠ACD＝∠B＝30°.

在Rt△ACD中，AC＝2AD＝6 cm，

在Rt△ABC中，AB＝2AC＝12 cm.∴ AB的长度是12 cm.

故选D.

例2　[教材P5例3] 如图20，在A岛周围20海里水域内有暗礁，一轮船由西向东航行到O处时，测得A岛在北偏东60°的方向，且与轮船相距30 海里．若该船继续保持由西向东的航向，那么有触礁的危险吗？

图20 

变式一　如图21所示，某船于上午11时30分在A处观察海岛B位于北偏东60°，该船以每小时10海里的速度向东航行至C处，再观察海岛位于北偏东30°，且船距离海岛20海里．

图21 

(1)求该船到达C处的时刻；

(2)若该船从C处继续向东航行，何时到达B岛正南方向的D处？

[答案：(1)13时30分　(2)14时30分]

例3  如图22，已知:等腰三角形的底角为15 °，腰长为20.求腰上的高.

解：过C作CD⊥BA，交BA的延长线于点D.

∵ ∠B＝∠ACB＝15°（已知），

∴ ∠DAC＝∠B+∠ACB＝15°+15°＝30°，∴ CD＝AC＝×20＝10.

图22

教师引导总结：在求三角形边长的问题中，可以构造含30°角的直角三角形．本题的关键是作高，再利用等腰三角形及外角的性质得出30°角，利用含30°角的直角三角形的性质解决问题.

课堂小结

布置作业

教材第7页习题1.1A组第3，4，5题，B组第8题.

板书设计

1.1  直角三角形的性质和判定(Ⅰ)

第2课时  含30°锐角的直角三角形的性质及其应用

1.在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.

2.在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于30°.

例1

例2

例3