


湘教版八年级下册1.1 直角三角形的性质与判定(Ⅰ)完美版ppt课件
展开1.了解直角三角形两个锐角的关系.(重点)
2.掌握直角三角形的判定及推论.(难点)
3.会运用直角三角形的性质和判定进行相关计算.(难点)
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷.你知道其中的道理吗?
老大的度数为90°,老二若是比老大的度数大,那么老二的度数要大于90°,而三角形的内角和为180°,相互矛盾,因而是不可能的.
在这个家里,我是永远的老大.
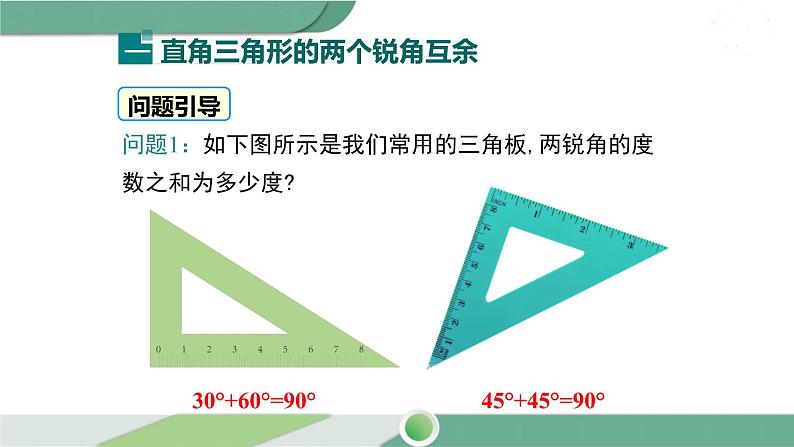
问题1:如下图所示是我们常用的三角板,两锐角的度数之和为多少度?
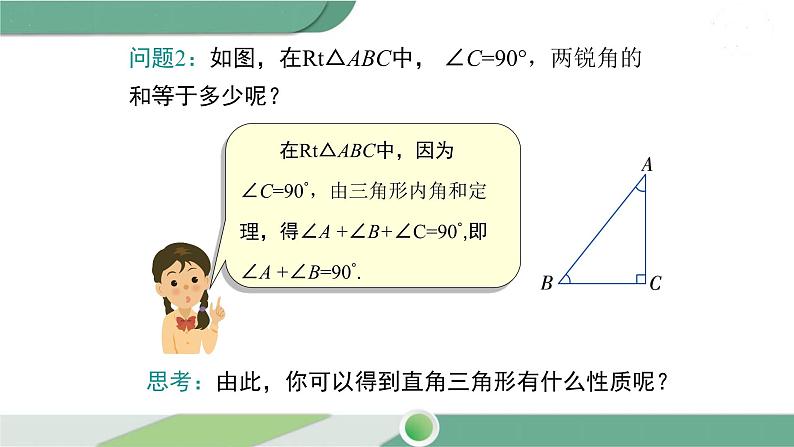
问题2:如图,在Rt△ABC中, ∠C=90°,两锐角的和等于多少呢?
思考:由此,你可以得到直角三角形有什么性质呢?
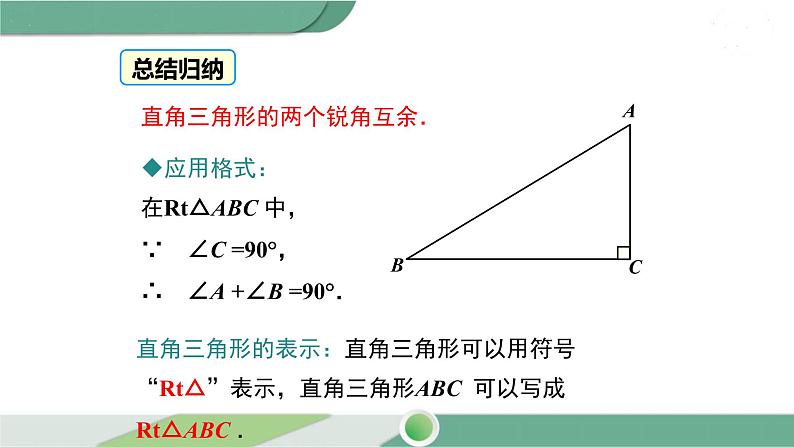
直角三角形的两个锐角互余.
应用格式:在Rt△ABC 中,∵ ∠C =90°,∴ ∠A +∠B =90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC .
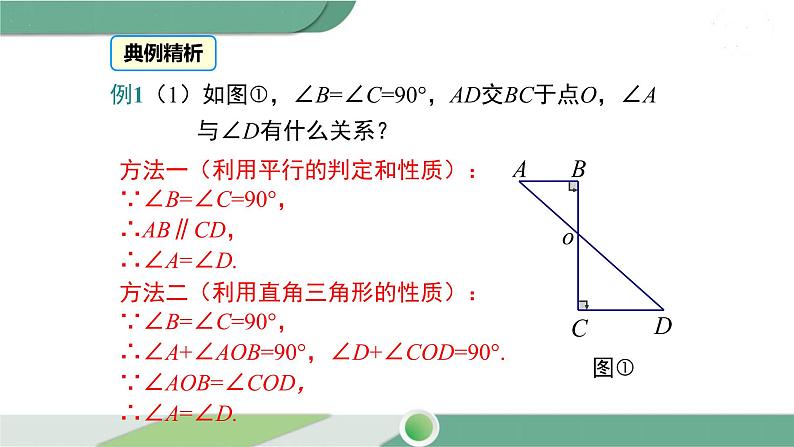
方法一(利用平行的判定和性质):∵∠B=∠C=90°,∴AB∥CD,∴∠A=∠D.方法二(利用直角三角形的性质):∵∠B=∠C=90°,∴∠A+∠AOB=90°,∠D+∠COD=90°.∵∠AOB=∠COD,∴∠A=∠D.
例1(1)如图,∠B=∠C=90°,AD交BC于点O,∠A 与∠D有什么关系?
解:∠A=∠C.理由如下:∵∠B=∠D=90°,∴∠A+∠AOB=90°,∠C+∠COD=90°.∵∠AOB=∠COD,∴∠A=∠C.
(2)如图,∠B=∠D=90°,AD交BC于点O,∠A与 ∠C有什么关系?请说明理由.
与图有哪些共同点与不同点?
例2 如图, ∠C=∠D=90 °,AD,BC相交于点E. ∠CAE与∠DBE有什么关系?为什么?
解:在Rt△ACE中, ∠CAE=90 °- ∠AEC.
在Rt△BDE中, ∠DBE=90 °- ∠BED.
∵ ∠AEC= ∠BED,∴ ∠CAE= ∠DBE.
解:∵CD⊥AB于点D,BE⊥AC于点E, ∴∠BEA=∠BDF=90°, ∴∠ABE+∠A=90°, ∠ABE+∠DFB=90°. ∴∠A=∠DFB. ∵∠DFB+∠BFC=180°, ∴∠A+∠BFC=180°.
【变式题】如图,△ABC中,CD⊥AB于D,BE⊥AC于E,CD,BE相交于点F,∠A与∠BFC又有什么关系?为什么?
思考:通过前面的例题,你能画出这些题型的基本 图形吗?
问题:有两个角互余的三角形是直角三角形吗?
如图,在△ABC中, ∠A +∠B=90° , 那么△ABC是直角三角形吗?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
应用格式:在△ABC 中,∵ ∠A +∠B =90°,∴ △ABC 是直角三角形.
有两个角互余的三角形是直角三角形.
例3 如图,∠C=90 °, ∠1= ∠2,△ADE是直角三 角形吗?为什么?
解:在Rt△ABC中, ∠2+ ∠A=90 °.
∵ ∠1= ∠2, ∴∠1 + ∠A=90 °.
即△ADE是直角三角形.
例4 如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是 直角三角形吗?为什么?
解:△ABD是直角三角形.理由如下:∵CE⊥AD,∴∠CED=90°,∴∠C+∠D=90°,∵∠A=∠C,∴∠A+∠D=90°,∴△ABD是直角三角形.
问题: 如图,画一个Rt△ABC, 并作出斜边AB上的中线CD,比较线段CD 与线段AB 之间的数量关系,你能得出什么结论?
线段CD 比线段AB短.
猜想:直角三角形斜边上的中线等于斜边的一半.
∴ 点D'是斜边上的中点,即CD' 是斜边AB的中线.
直角三角形斜边上的中线等于斜边的一半.
例5 已知:如图,CD是△ABC的AB边上的中线,且 . 求证:△ABC是直角三角形.
∴ ∠1=∠A,∠2=∠B .
∵∠A+∠B+∠ACB =180°,即∠A+∠B+∠1+∠2=180°, 2(∠A+∠B)=180°.
∴ ∠A+∠B =90°.
∴ △ABC是直角三角形.
例6 如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.(1)若AB=10,AC=8,求四边形AEDF的周长;
解:∵AD是△ABC的高,E、F分别是AB、AC的中点,∴DE=AE= AB= ×10=5, DF=AF= AC= ×8=4,∴四边形AEDF的周长=AE+DE+DF+AF =5+5+4+4=18;
(2)求证:EF垂直平分AD.
证明:∵DE=AE,DF=AF,∴E、F在线段AD的垂直平分线上, ∴EF垂直平分AD.
当已知条件含有线段的中点、直角三角形的条件时,可联想直角三角形斜边上的中线的性质进行求解.
如图,在△ABC中,∠ABC = 90°,BD是斜边AC上的中线.(1)若BD=3cm,则AC =_____cm;(2)若∠C = 30° ,AB = 5cm,则AC =_____cm, BD = _____cm.
体现直角三角形斜边上中线的性质的常见图形
1.如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1+∠2的度数是________.
2.如图,AB、CD相交于点O,AC⊥CD于点C, 若∠BOD=38°,则∠A=________.
3.在△ABC中,若∠A=43°,∠B=47°,则这个三角形是____________.
4.在一个直角三角形中,有一个锐角等于40°,则另 一个锐角的度数是( ) A.40° B.50° C.60° D.70°
5.具备下列条件的△ABC中,不是直角三角形的是 ( )A.∠A+∠B=∠C B.∠A-∠B=∠C C.∠A:∠B:∠C=1:2:3 D.∠A=∠B=3∠C
6.如图所示,△ABC为直角三角形,∠ACB=90°, CD⊥AB,与∠1互余的角有( )A.∠B B.∠A C.∠BCD和∠A D.∠BCD
7.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.求证:△ACD是直角三角形.
证明:∵∠ACB=90°,∴∠A+∠B=90°,∵∠ACD=∠B,∴∠A+∠ACD=90°,∴△ACD是直角三角形.
8. 如图,已知BD,CE是△ABC不同边上的高,点G,F分别是BC,DE的中点,试说明GF⊥DE.
解:连接EG,DG. ∵BD,CE是△ABC的高, ∴∠BDC=∠BEC=90°. ∵点G是BC的中点,∴EG= BC,DG= BC. ∴EG=DG. 又∵点F是DE的中点, ∴GF⊥DE.
在直角三角形中,遇到斜边中点常作斜边中线,进而可将问题转化为等腰三角形的问题,然后利用等腰三角形“三线合一”的性质解题.
湘教版八年级下册1.1 直角三角形的性质与判定(Ⅰ)教案配套ppt课件: 这是一份湘教版八年级下册1.1 直角三角形的性质与判定(Ⅰ)教案配套ppt课件,共15页。PPT课件主要包含了∠A+∠B90°,知识回顾,新知探究,直角三角形性质定理,图形语言,新知归纳,这样构成等边△ADB,疑问升级,于是得到逆定理,例题讲解等内容,欢迎下载使用。
初中数学1.1 直角三角形的性质与判定(Ⅰ)课文课件ppt: 这是一份初中数学1.1 直角三角形的性质与判定(Ⅰ)课文课件ppt,共16页。PPT课件主要包含了有3个直角三角形,知识回顾,∵∠C90°,新知探究,成立吗,∴∠C=900,等腰直角,随堂练习,AD+DB,我们来验证一下等内容,欢迎下载使用。
湘教版八年级下册1.1 直角三角形的性质与判定(Ⅰ)优秀ppt课件: 这是一份湘教版八年级下册1.1 直角三角形的性质与判定(Ⅰ)优秀ppt课件,文件包含教学课件八下·湘教·11直角三角形的性质和判定Ⅰ第1课时直角三角形的性质和判定pptx、11直角三角形的性质和判定Ⅰ第1课时教案docx、11直角三角形的性质和判定Ⅰ第1课时同步练习docx等3份课件配套教学资源,其中PPT共25页, 欢迎下载使用。














