初中华师大版2. 圆的对称性一等奖课件ppt

教学目标

1.进一步认识圆，了解圆是轴对称图形.

2.理解垂直于弦的直径的性质和推论，并能应用它解决一些简单的计算、证明和作图问题.

教学重难点

重点:理解垂直于弦的直径的性质和推论，并能应用它解决一些简单的计算、证明和作图问题.

难点：灵活运用垂径定理解决有关圆的问题.

教学过程

导入新课

由问题引入新课：要同学们画两个等圆，并把其中一个圆剪下，让两个圆的圆心重合，使得其中一个圆绕着圆心旋转，可以发现，两个圆都是互相重合的.如果沿着任意一条直径所在的直线折叠，圆在这条直线两旁的部分会完全重合.

探究新知

合作探究

1.垂径定理

问题情境： 如图，AB是⊙O的一条弦，直径CD⊥AB, 垂足为E.你能发现图中有哪些相等的线段和劣弧?

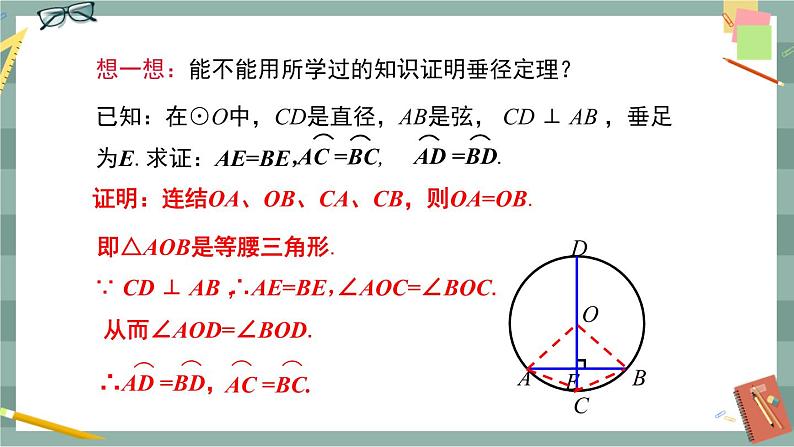
师生活动：学生独立思考并找出图中相等的线段和劣弧，教师巡视并指导.

【解】相等线段: AE＝BE.

相等劣弧：＝,＝.

理由：连结OA,OB，把圆沿着直径CD折叠时，CD两侧的两个半圆重合，点A与点B重合，AE与BE重合，与重合，与重合.             

教师追问：你能用语言来描述我们的发现吗？

师生活动：学生小组交流讨论，师生归纳，教师最后整理并板书.

【归纳总结】垂径定理：垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.

教师追问：能不能用所学过的知识证明垂径定理？

师生活动：(引发学生思考)要证明垂径定理，已知条件是什么？结论是什么？用什么方法证明?

【解】已知：如图，在⊙O中，CD是⊙O的直径，AB是弦，AB⊥CD，垂足为E.

求证：AE＝BE，.

证明：（方法1）如图，连结OA，OB.

∵ OA＝OB，CD⊥AB，

∴AE＝BE.

又∵ ⊙O关于直径CD所在直线对称，

∴ A点和B点关于直径CD所在直线对称，

∴当圆沿着直径CD所在直线对折时，点A与点B重合，与重合，

因此.

同理得到.

（方法2）连结OA，OB，CA，CB，则OA=OB.

即△AOB是等腰三角形.

∵AB⊥CD，∴AE=BE，∠AOD=∠BOD.

从而∠AOC=∠BOC.

∴,.

【归纳总结】根据图形写出已知和求证，再构造等腰三角形，利用等腰三角形 “三线合一”的性质，从而证得结论成立.

推导格式

∵ CD是⊙O的直径，CD⊥AB，垂足为E，

∴ AE＝BE，.

定理辨析：下列图形是否具备垂径定理的条件？如果不是，请说明为什么？

①                ②            ③           ④

师生活动：(引发学生思考)垂径定理具备的条件.

【解】图①具备；图②不具备，因为没有垂直；图③具备；图④不具备，因为没过圆心.

【归纳总结】(学生总结，老师点评)垂径定理具备的条件是过圆心且垂直，两个条件缺一不可.

【归纳】垂径定理的几个基本图形：

①                 ②           ③           ④

2.垂径定理的推论

（1）平分弦（不是直径）的直径垂直于这条弦，并且平分这条弦所对的两条弧.

推导格式

（2）平分弧的直径垂直平分这条弧所对的弦.

推导格式

教师追问：“不是直径”这个条件能去掉吗？如果不能，请举出反例.

师生活动：学生独立思考并举反例，师生共同归纳.

【归纳总结】圆的两条直径是互相平分的，但是不一定相互垂直.                                           

一条直线满足下面五个条件中的两个条件，即可推出其他三个.

①过圆心；

②垂直于弦；

③平分弦（非直径）；

④平分弦所对优弧；

⑤平分弦所对劣弧.

【新知应用】

例1　如图，⊙O的弦AB＝8 cm ，直径CE⊥AB于点D，DC＝2 cm，求半径OC的长.

师生活动：学生尝试解决，教师引导.求OC，即求半径，可在Rt△AOD中利用勾股定理求得.

【解】如图，连结OA.

∵ CE⊥AB 于点D，

∴.

设OC＝x cm，则OD ＝（x-2）cm.

根据勾股定理，得.

 ，解得x＝5.

即半径OC 的长为5 cm.

【归纳总结】在圆中解决有关弦长、半径等问题，常常需要作垂直于弦的直径或半径，连结弦的端点与圆心作半径，这样就可以把垂径定理与勾股定理结合起来，得到圆的半径r、弦心距d、弦长a的一半之间的关系式：.

【拓展延伸】　

例2　已知⊙O的半径为13，弦AB＝24，弦CD＝10，AB∥CD，求这两条平行弦AB，CD之间的距离.

师生活动：(引发学生思考)要求两条平行弦AB，CD之间的距离，想到垂直，又在圆中已知弦长，则可以想到垂径定理和勾股定理，由此根据这些怎么作图呢？根据题中数据怎样求解呢？

【解】分两种情况讨论：（1）当弦AB和CD在圆心同侧时，如图①，过点O作OF⊥CD于点F，交AB于点E，连结OC，OA.

由题意可知，OA＝OC＝13.

∵ AB∥CD，OF⊥CD，∴OE⊥AB.

又∵ AB＝24，CD＝10，

∴ AE＝ AB＝12，CF＝ CD＝5，

∴ OE＝＝5，OF＝＝12，

∴ EF＝OF-OE＝7.

（2）当弦AB和CD在圆心异侧时，如图②，过点O作OF⊥CD于点F，反向延长OF交AB于点E，连结OC，OA.

同(1)可得，OE＝5，OF＝12，∴EF＝OF+OE＝17.

综上，两条平行弦AB与CD之间的距离为7或17.

①           ②

【归纳总结】(学生总结，老师点评)解此类题时，要考虑两弦在圆心的同侧还是异侧，再结合实际作出半径和弦心距（圆心到弦的距离），利用勾股定理和垂径定理求解即可.

练一练

已知⊙O的直径是50 cm，⊙O的两条平行弦AB=40 cm ，CD=48cm，求弦AB与CD之间的距离.

师生活动：（学生尝试画图，教师引导）当弦的位置不能确定时，要进行分类讨论.

答案：8cm或22cm

例3　一根横截面为圆形的下水管道的直径为1米，管内有少量的污水(如图)，此时的水面宽AB为0.6米，求此时的水深(即阴影部分弓形的高).

师生活动：学生先审题，可以小组讨论，教师引导学生思考，要求此时的水深，即阴影部分弓形的高，结合垂径定理，考虑怎样作辅助线才能得到水深？

【解】如图，过点O作OD⊥AB于点C，交⊙O于点D，连结OB.

根据垂径定理，得点C是AB的中点，点D是的中点，则BC＝ AB＝0.3米.

由题意，知OD＝OB＝0.5米，

在Rt△OBC中，由勾股定理，得OC＝ ＝0.4米，

所以CD＝OD -OC＝0.1米，

即此时的水深为0.1米.

【归纳总结】(学生总结，老师点评)在圆中求半径、弦等线段的长时，常常借助垂径定理构造直角三角形，再在直角三角形中运用勾股定理来解决.

例4　有一石拱桥的桥拱是圆弧形，如图所示，正常水位下水面宽AB＝60 m，水面到拱顶距离CD＝18 m，当洪水泛滥时，水面到拱顶距离为3.5 m时需要采取紧急措施，当水面宽MN＝32 m时是否需要采取紧急措施?请说明理由.

师生活动：(引发学生思考)求当水面宽MN＝32 m时是否需要采取紧急措施，即求此时水面到拱顶的距离为多少.怎样求出这个距离？

【解】不需要采取紧急措施.

理由如下：如图，设圆心为O，连结OM，OA，OD，OD与MN，AB分别交于点E，C.设OA＝R m.

由题意知，在Rt△AOC中，AC＝ AB＝30 m，CD＝18 m，

由勾股定理，得，R2＝302+(R-18)2，解得R＝34.

在Rt△MOE中，ME＝MN＝16 m，

∴ OE＝＝＝30（m），

∴ DE＝OD-OE＝4 m.

∵ 4＞3.5，∴ 不需要采取紧急措施.

【归纳总结】(学生总结，老师点评)解此类题时，要注意根据垂径定理，利用半径、半弦长、弦心距构造直角三角形，结合勾股定理求解.

【拓展归纳】

（1）涉及垂径定理时辅助线的添加方法

在圆中有关弦长a，半径r， 弦心距d（圆心到弦的距离），弓形高h的计算题时，常常通过连半径或作弦心距构造直角三角形，利用垂径定理和勾股定理求解.

（2）弓形中重要数量关系：弦长a，弦心距d，弓形高h，半径r之间有以下关系： .

课堂小结

1. 垂径定理

垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.

2. 垂径定理的推论

平分弦（不是直径）的直径垂直于这条弦，并且平分这条弦所对的两条弧；

平分弧的直径垂直平分这条弧所对的弦.

布置作业

教材第40页练习第1，2题.

第45页习题27.1第3题

板书设计

27.1 圆的认识

2  圆的对称性

（第2课时　垂径定理）

1.垂径定理

垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.

推导格式

∵ CD是直径，CD⊥AB，垂足为E，

∴ AE＝BE，.

2.垂径定理的推论

平分弦（不是直径）的直径垂直于这条弦，并且平分这条弦所对的两条弧；

推导格式

平分弧的直径垂直平分这条弧所对的弦.

推导格式

 3.方法：将垂径定理与勾股定理有机结合，化圆中问题为三角形问题，经常需要添加辅助线——半径、过圆心作弦的垂线.