2022-2023学年广东省广州市海珠外国语实验中学高一上学期段考（二）数学试题（解析版）

这是一份2022-2023学年广东省广州市海珠外国语实验中学高一上学期段考（二）数学试题（解析版），共15页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．函数的定义域为（ ）
A．B．
C．D．
【答案】D
【分析】根据开偶数次方根号里的数大于等于零，对数的真数大于零列出不等式组，即可得解.
【详解】解：由题意得，，解得，
所以函数的定义域为.
故选：D．
2．扇子最早称“翣”，其功能并不是纳凉，而是礼仪器具，后用于纳凉､娱乐､欣赏等.扇文化是中国传统文化的重要门类，扇子的美学也随之融人到建筑等艺术审美之中.图1为一古代扇形窗子，此窗子所在扇形的半径（图2），圆心角为，且为的中点，则该扇形窗子的面积为（ ）
A．B．
C．D．
【答案】B
【分析】根据扇形面积公式进行求解即可.
【详解】因为为的中点，所以化成弧度为，所以此扇形窗子的面积为
故选：B
3．函数的零点一定位于下列哪个区间（ ）
A．B．C．D．
【答案】B
【分析】根据零点存在性定理，即可求解.
【详解】由题意可知，，，
故，
又因函数在上单调递增，
所以函数的零点一定位于区间.
故选：B.
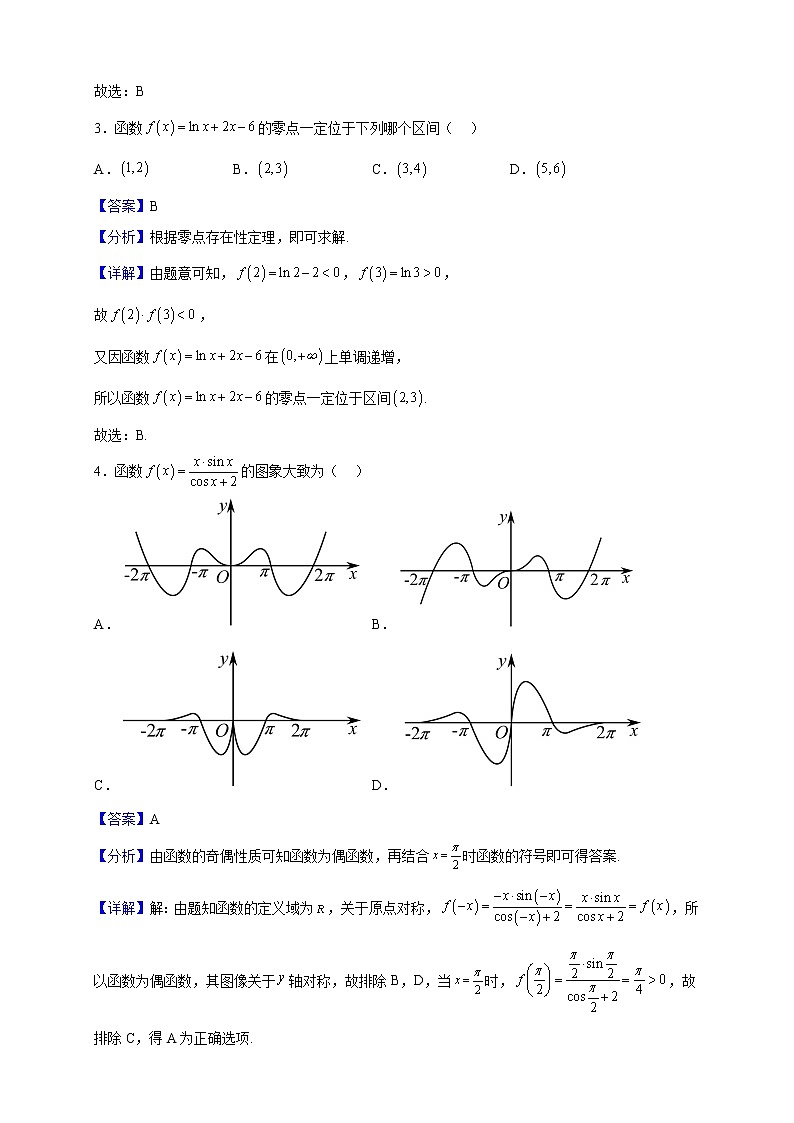
4．函数的图象大致为（ ）
A．B．
C．D．
【答案】A
【分析】由函数的奇偶性质可知函数为偶函数，再结合时函数的符号即可得答案.
【详解】解：由题知函数的定义域为，关于原点对称，，所以函数为偶函数，其图像关于轴对称，故排除B，D，当时，，故排除C，得A为正确选项.
故选：A
5．已知，则等于
A．B．C．D．
【答案】C
【分析】由诱导公式化简后即可求值．
【详解】＝-sin[]＝
故选C．
【点睛】本题主要考查了三角函数诱导公式的应用，属于基础题．
6．若，，，则有（ ）
A．B．C．D．
【答案】A
【解析】利用指数函数和对数函数的单调性比较、、三个数与、的大小关系，从而可得出这三个数的大小关系.
【详解】指数函数为增函数，则；
对数函数为增函数，则，即；
对数函数为增函数，则.
因此，.
故选：A.
【点睛】本题考查指数式与对数式的大小比较，一般利用指数函数和对数函数的单调性得出各数与中间值、的大小关系，考查推理能力，属于基础题.
7．已知偶函数f (x)在区间 单调递增，则满足的 x 取值范围是（ ）
A．B．C．D．
【答案】A
【分析】由偶函数性质得函数在上的单调性，然后由单调性解不等式．
【详解】因为偶函数在区间上单调递增，
所以在区间上单调递减，故越靠近轴，函数值越小，
因为，
所以，解得：.
故选：A．
8．已知函数且在上无零点，在上有零点，则实数的取值范围为（ ）
A．B．
C．D．
【答案】D
【分析】将问题转化成研究方程在上无实数根，在上有实数根，即考查函数的交点情况，作出函数图像数形结合即可得到答案.
【详解】函数在上无零点，在上有零点，
即方程在上无实数根，在上有实数根，
即在上无实数根，在上有实数根，设，
函数在上单调递增，且，
恒成立，若，则在时，，故不满足条件.
由于与的图象在上无交点，在上有交点，
根据函数的图像可知，解得
故选：D.
二、多选题
9．已知幂函数，则（ ）
A．B．定义域为
C．D．
【答案】AC
【分析】根据为幂函数得可判断A；根据幂函数的解析式可判断B；利用单调性可判断C；
计算可判断D.
【详解】为幂函数，，得，A对；
函数的定义域为，B错误；
由于在上为增函数，，C对；
，，D错误，
故选：AC.
10．下列选项中，正确的是（ ）
A．函数（且）的图象恒过定点
B．若不等式的解集为，则
C．若：，，则：，
D．函数恰有1个零点
【答案】BCD
【分析】对于A，根据指数函数的图像与性质即可求解；对于B，根据一元二次不等式的解法即可判断；对于C，由特称命题的否定为全称命题即可得出结论；对于D，由函数零点存在定理和函数单调性即可求解.
【详解】对A：函数（且）的图象恒过定点，即A错误；
对B: 若不等式的解集为，
则，且和是方程的两个实数根，
所以，解得，所以，即B正确；
对于C：若：，，则：，，故C选项正确；
对于D：易知函数在上为单调递增，
又，；
所以由函数零点存在定理可得存在唯一，使得；
所以，D正确.
故选：BCD.
11．下列既是奇函数，又在上是增函数的是（ ）
A．B．
C．D．
【答案】AC
【分析】对于ABC，根据函数的定义域、奇偶性及单调性等性质即可判断.
对于D，根据奇偶函数的定义和复合函数单调性即可得出D错误.
【详解】对于A，的定义域为，，则为奇函数，由幂函数的性质知： 在上单增，所以A正确.
对于B，的定义域为，，所以不是奇函数，所以B错误.
对于C，的定义域为，，则为奇函数，又因为，为增函数，为减函数，为增函数， 为增函数，所以C正确.
对于D，有解得：.
，则
是奇函数，令在区间上单调递减，而为增函数，故在上是减函数，所以D错误.
故选：AC.
12．已知函数函数有四个不同的零点，，，，且，则（ ）
A．的取值范围是B．的取值范围是
C．D．
【答案】AC
【分析】结合的图象，由图可知，，，由二次函数的对称性，可得，可得答案.
【详解】有四个不同的零点，，，，即方程有四个不同的解．
的图象如图所示，由图可知，，，所以，
即的取值范围是，
由二次函数的对称性，可得．因为，所以，故．
故选：AC.
三、填空题
13．计算：______．
【答案】
【分析】利用诱导公式即得.
【详解】．
故答案为：.
14．声强级L（单位：dB）由公式给出，其中I为声强（单位：W/m2）. 声强级为60dB的声强是声强级为30dB的声强的______倍.
【答案】1000
【分析】根据已知公式，应用指对数的关系及运算性质求60dB、30dB对应的声强，即可得结果.
【详解】由题设，，可得，
，可得，
∴声强级为60dB的声强是声强级为30dB的声强的倍.
故答案为：1000.
15．已知定义在上的减函数满足是其图象上一点，那么的解集为__________.
【答案】（
【分析】由题意可得，结合条件，利用奇偶性和单调性可解出不等式，得到答案.
【详解】由知为奇函数，
由即
又，
又知函数在上为减函数，可得，
解得解集为.
故答案为：
16．设a为实数，若关于x的方程有实数解，则a的取值范围是___________.
【答案】
【分析】令，将原问题转化为方程有正根，利用判别式及韦达定理列出不等式组求解即可得答案.
【详解】解：方程可化为，令，则，
所以原问题转化为方程有正根，设两根分别为，
则，解得，
所以的取值范围是，
故答案为：.
四、解答题
17．（1）计算：；
（2）已知，求的值．
【答案】（1）1
（2）2
【分析】（1）利用指数、对数的运算及其运算性质计算求解.
（2）分子分母同时除以，把弦化切进行求解.
【详解】（1）原式=
=
=
=1
（2）因为，且，
所以分子分母同除以有：
，
即，
解得 .
18．已知集合.
（1）求集合,；
（2）若集合且,求的取值范围.
【答案】（1）,；（2）.
【详解】试题分析：（1）利用一元二次不等式的解法化简集合，利用指数函数的性质化简集合，从而可求出，再利用集合交集与并集的定义求解即可；（2）等价于，结合（1）的结论，利用集合的包含关系，分两种情况讨论，分别列不等式组求解即可求得的取值范围.
试题解析：（1）,
∴，,
∴.
（2）∵，，,
当时，时满足∴;
当时，要使，则
综上所述，.
19．已知函数是定义在上的偶函数，当时，.
(1)求函数的解析式；
(2)解不等式.
【答案】(1)
(2)
【分析】(1)根据函数的奇偶性即可求得函数在时的解析式；
(2)根据(1)中的函数解析式判断函数的单调性，利用函数的奇偶性解不等式即可.
【详解】（1）设，则，
是定义在R上的偶函数，
，
；
（2）由（1）知，时，，
与在上都是增函数，
在上为增函数，在上为减函数，
，
解得.
该不等式的解集为.
20．已知函数是定义在R上的奇函数．
(1)用定义法证明为增函数；
(2)对任意，都有恒成立，求实数k的取值范围．
【答案】(1)证明见解析
(2)
【分析】（1）根据函数单调性的定义及指数函数的单调性与值域即可证明；
（2）由已知条件，利用函数的奇偶性和单调性，可得对恒成立，然后分离参数，利用基本不等式求出最值即可得答案.
【详解】（1）证明：设，则，
由，可得，即，又，，
所以，即，则在上为增函数；
（2）解：因为任意，都有恒成立，且函数是定义在R上的奇函数，
所以对恒成立，
又由（1）知函数在上为增函数，所以对恒成立，
由，有，
所以对恒成立，
设，由在递减，可得，
所以，当且仅当时取得等号，
所以，即的取值范围是.
21．为保护环境，污水进入河流前都要进行净化处理.我市工业园区某工厂的污水先排入净化池，然后加入净化剂进行净化处理.根据实验得出，在一定范围内，每放入1个单位的净化剂，在污水中释放的浓度y（单位：毫克/立方米）随着时间x（单位：小时）变化的函数关系式近似为.若多次加进净化剂，则某一时刻净化剂在污水中释放的浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知，当净化剂在污水中释放的浓度不低于4（毫克/立方米）时，它才能起到净化污水的作用.
(1)若投放1个单位的净化剂4小时后，求净化剂在污水中释放的浓度；
(2)若一次投放4个单位的净化剂并起到净化污水的作用，则净化时间约达几小时？（结果精确到0.1，参考数据：，）
(3)若第一次投放1个单位的净化剂，3小时后再投放2个单位的净化剂，设第二次投放t小时后污水中净化剂浓度为（毫克/立方米），其中，求的表达式和浓度的最小值.
【答案】(1)6毫克/立方米
(2)7.1
(3)，； 的最小值为12毫克/立方米
【分析】（1）由函数解析式，将代入即可得解；
（2）分和两种情况讨论，根据题意列出不等式，从而可得出答案；
（3）根据题意写出函数的解析式，再根据基本不等式即可求得最小值.
【详解】（1）解：由，
当时，，
所以若投放1个单位的净化剂4小时后，净化剂在污水中释放的浓度为6毫克/立方米；
（2）解：因为净化剂在污水中释放的浓度不低于4（毫克/立方米）时，它才能起到净化污水的作用，
当时，令，得恒成立，
所以当时，起到净化污水的作用，
当时，令，得，则，
所以，
综上所述当时，起到净化污水的作用，
所以若一次投放4个单位的净化剂并起到净化污水的作用，则净化时间约达7.1小时；
（3）解：因为第一次投入1个单位的净化剂，3小时后再投入2个单位净化剂，要计算的是第二次投放t小时后污水中净化剂浓度为，
所以，，
因为，
所以，
当且仅当，即时取等号，
所以，，
当时，取最小值12毫克/立方米.
22．对于函数，若在其定义域内存在实数x，满足，则称为“局部奇函数”．
(1)若是定义在区间上的“局部奇函数”，求实数m的取值范围．
(2)若为定义域R上的“局部奇函数”，求实数n的取值范围．
【答案】(1)
(2)
【分析】（1）根据是定义在区间上的“局部奇函数”可知，由此求出m的解析式，利用换元法，构造函数，求出函数的值域，即可求得m的取值范围.
（2）根据是定义在区间R上的“局部奇函数”可知，由此求出n的解析式，利用换元法，构造函数，求出函数的值域，即可求得n的取值范围.
【详解】（1）解：因为是定义在区间上的“局部奇函数”
所以，即
所以
于是问题转换成方程在有解
令，，则
所以在上有解
根据在为减函数，在为增函数，且，
所以，即，解得
所以实数m的取值范围为；
（2）因为是定义在区间R上的“局部奇函数”
所以，即
整理可得：
令，则
又
所以方程在上有解
设，
当时，在上有解，此时，解得：
当时，在上有解，此时，解得：;
综上所述：实数n的取值范围.