
2022-2023学年七年级数学上学期期末【夯实基础100题考点专练】
展开七年级上学期期末【夯实基础100题考点专练】
一、单选题
1.(2022·江苏泰州·七年级期末)下列所给数据中,能反映出一瓶矿泉水重量的是( ).
A.500毫克 B.500克 C.500千克 D.500吨
2.(2022·江苏淮安·七年级期末)下列四个数中,无理数是( )
A. B.π C.0.12 D.0
3.(2022·江苏盐城·七年级期末)的倒数是( )
A. B. C. D.
4.(2022·江苏宿迁·七年级期末)能说明命题“任何数a的平方都大于0.”是假命题的一个反例可以是( )
A. B. C. D.
5.(2022·江苏镇江·七年级期末)下列计算正确的是( )
A.﹣2+3=5 B.﹣7﹣(﹣4)=﹣3
C. D.(﹣)÷(﹣8)=1
6.(2022·江苏南通·七年级期末)规定:表示向右移动2,记作+2,则表示向左移动5,记作( )
A.+5 B.-5 C. D.-
7.(2022·江苏扬州·七年级期末)当前手机移动支付已经成为新型的支付方式,图中是妈妈元旦当天的微信零钱支付明细,则妈妈元旦当天的微信零钱收支情况是( )
转账﹣来自SNM
+48
云视听极光
﹣30
扫二维码付款
﹣50
A.收入128元 B.收入32元 C.支出128元 D.支出32元
8.(2022·江苏苏州·七年级期末)下列计算正确的是( )
A. B. C. D.
9.(2022·江苏无锡·七年级期末)下列计算正确的是( )
A. B.
C. D.
10.(2022·江苏南通·七年级期末)计算﹣(4a﹣5b),结果是( )
A.-4a-5b B.-4a+5b C.4a-5b D.4a+5b
11.(2022·江苏南通·七年级期末)若与是同类项,则的值为( )
A.-1 B.-5 C.5 D.7
12.(2022·江苏南京·七年级期末)是下面哪个二元一次方程的解( )
A. B. C. D.
13.(2022·江苏无锡·七年级期末)下列方程为一元一次方程的是( )
A. B. C. D.
14.(2022·江苏南京·七年级期末)将如图所示的长方形绕它的对角线所在直线旋转一周,形成的几何体是( )
A. B. C. D.
15.(2022·江苏无锡·七年级期末)如图是一个小正方体的表面展开图,把展开图折叠成小正方体后,有“开”字一面的相对面上的字是( )
A.我 B.爱 C.教 D.育
16.(2022·江苏宿迁·七年级期末)如图,下列几何体中,主视图和俯视图相同的是( )
A. B.
C. D.
17.(2022·江苏宿迁·七年级期末)某正方体的每一个面上都有一个汉字,如图是它的种表面展开图,那么在原正方体的表面上,与“洗”字相对的面上的汉字是( )
A.罩 B.勤 C.口 D.戴
18.(2022·江苏南京·七年级期末)如图是一个几何体的侧面展开图,则该几何体是( )
A.三棱柱 B.三棱锥 C.五棱柱 D.五棱锥
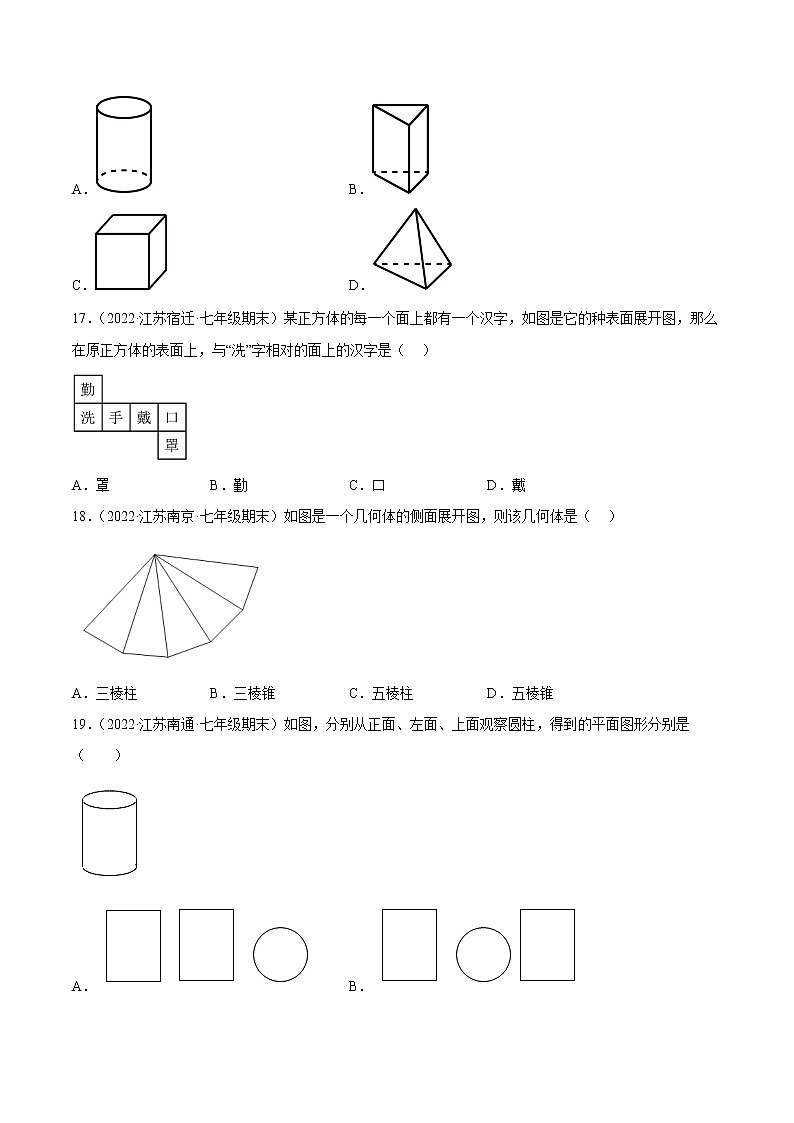
19.(2022·江苏南通·七年级期末)如图,分别从正面、左面、上面观察圆柱,得到的平面图形分别是( )
A. B.
C. D.
20.(2022·江苏无锡·七年级期末)如图,C、D是线段AB上两点,且,则AC与BD的关系是( )
A. B. C. D.
21.(2022·江苏无锡·七年级期末)若∠1与∠2互余,∠1与∠3互补,则∠2与∠3的关系是( )
A. B. C. D.
22.(2022·江苏常州·七年级期末)如图,已知A、B、C三点,过点A可画直线BC的平行线的条数是( )
A.0条 B.1条 C.2条 D.无数条
23.(2022·江苏南京·七年级期末)如图,,,垂足分别为C、D,线段的长度是( )
A.点A到的距离 B.点B到的距离
C.点C到的距离 D.点D到的距离
24.(2022·江苏盐城·七年级期末)要在墙上固定一根木条,小明说只需要两根钉子,这其中用到的数学道理是( )
A.两点之间线段最短 B.两点确定一条直线
C.垂线段最短 D.两条直线相交,只有一个交点
25.(2022·江苏无锡·七年级期末)下列人或物中,质量最接近1吨的是( )
A.1000枚1元硬币 B.25名小学生
C.5000个鸡蛋 D.10辆家用轿车
26.(2022·江苏扬州·七年级期末)的相反数是( )
A. B. C. D.
27.(2022·江苏扬州·七年级期末)下列代数式的值一定是正数的是( )
A. B. C. D.
28.(2022·江苏南京·七年级期末)据统计,电影《长津湖》上映第16天,累计票房突破45.6亿元.将数据45.6亿用科学记数法表示为( )
A.45.6×108 B.4.56×109 C.4.56×1010 D.0.456×1011
29.(2022·江苏扬州·七年级期末)已知a,b的位置如图,则的值为( )
A.0 B.-2b C.-2a D.2b-2a
二、填空题
30.(2022·江苏宿迁·七年级期末)某种细菌病毒的直径为0.000000505米,0.000000505米用科学记数法表示为____米.
31.(2022·江苏扬州·七年级期末)天宫二号是中国首个具备补加功能的载人航天科学实验空间实验室,天宫二号的轨道高度约为393000m,393000m用科学记数法表示为 _____m.
32.(2022·江苏扬州·七年级期末)单项式的系数是_____.
33.(2022·江苏南通·七年级期末)有一个两位数,个位数字是n,十位数字是m,则这个两位数可表示为__________.
34.(2022·江苏扬州·七年级期末)单项式的系数是____.
35.(2022·江苏扬州·七年级期末)若a,b互为倒数,则﹣4ab+1的值为______.
36.(2022·江苏宿迁·七年级期末)已知方程的解是,则k的值为 _____.
37.(2022·江苏扬州·七年级期末)当x=____时,代数式=4.
38.(2022·江苏南京·七年级期末)已知x=-1是方程2ax-5=a-2的解,则a=______.
39.(2022·江苏南京·七年级期末)写出一个解是,未知数的系数为3,且等号左边为多项式的一元一次方程_______.
40.(2022·江苏南京·七年级期末)三视图都是圆形的几何体是______.
41.(2022·江苏常州·七年级期末)如图所示是一个几何体的三视图,若这个几何体的体积是6,则它的表面积是________.
42.(2022·江苏南京·七年级期末)如图是一个正方体的表面展开图,每个面上都标有字母.其中与字母A处于正方体相对面上的是字母_______.
43.(2022·江苏淮安·七年级期末)如图,将一副三角板叠在一起,使它们的直角顶点O重合,若∠AOB=165°,则∠COD的度数为____.
44.(2022·江苏常州·七年级期末)如图,∠1=133°25′,AO⊥OB于点O,点C、O、D在一条直线上,则∠2的度数等于______.
45.(2022·江苏盐城·七年级期末)北京时间20点30分,此时钟表的时针和分针构成的角度是 _____°.
46.(2022·江苏盐城·七年级期末)下列生产和生活现象:①把弯曲的公路改直,就能缩短路程;②用两个钉子就可以把木条固定在墙上;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;④从A地到B地架设电线,总是尽可能沿着线段AB架设.其中能用“两点确定一条直线”来解释的现象有 _____.(填序号)
47.(2022·江苏宿迁·七年级期末)已知与互为补角,且,则_____.
48.(2022·江苏泰州·七年级期末)如图,OA表示北偏东20°方向的一条射线,OB表示南偏西50°方向的一条射线,则的度数是_____________.
49.(2022·江苏泰州·七年级期末)若,则的余角的度数是___________.
50.(2022·江苏宿迁·七年级期末)如图,在直线l上有A,B,C三点,则图中的线段共有 _____条.
51.(2022·江苏无锡·七年级期末)已知∠α=96°24′,则∠α的补角为______.
52.(2022·江苏·射阳县第六中学七年级期末)如图,想在河堤两岸搭建一座桥,搭建方式最短的是线段 _____.
53.(2022·江苏南京·七年级期末)比较大小:-______-,(填“>”、“<”或“=”)
54.(2022·江苏淮安·七年级期末)如图是一个数值运算程序,当输入的值为﹣2时,则输出的的值为 _____.
三、解答题
55.(2022·江苏无锡·七年级期末)计算:
(1); (2).
56.(2022·江苏盐城·七年级期末)计算:
(1) (2)
57.(2022·江苏淮安·七年级期末)计算:
(1)2×(﹣2)+3
(2)
58.(2022·江苏泰州·七年级期末)计算:
(1); (2).
59.(2022·江苏盐城·七年级期末)解下列方程:
(1); (2).
60.(2022·江苏南京·七年级期末)如图,是一个由7个正方体组成的立体图形.画出该立体图形的主视图、左视图和俯视图.
61.(2022·江苏扬州·七年级期末)有以下运算程序,如图所示:
比如,输入数对(2,1),输出W=2.
(1)若输入数对(1,﹣2),则输出W= ;
(2)分别输入数对(m,﹣n)和(﹣n,m),输出的结果分别是,试比较的大小,并说明理由;
(3)设a=|x+2|,b=|x﹣3|,若输入数对(a,b)之后,输出W=26,请直接写出a+2b的值.
62.(2022·江苏扬州·七年级期末)计算:
(1) (2)
63.(2022·江苏淮安·七年级期末)计算:
(1)﹣(﹣2)+5+|﹣9|; (2)﹣14﹣8÷(﹣4)×(﹣6+4).
64.(2022·江苏镇江·七年级期末)观察下列式子:
①,
②,
③,
……
(1)根据你发现的规律,请写出第个等式________;
(2)根据你发现的规律,请写出第(为正整数)个等式________,并证明你所写出的等式的正确性;
(3)请写出第198个等式:_________.
65.(2022·江苏盐城·七年级期末)先化简,再求值:2(3ab2﹣a2b+ab)﹣3(2ab2﹣4a2b+ab),其中a=﹣1,b=2.
66.(2022·江苏盐城·七年级期末)先化简,再求值:已知,,若的值为-8,求的值.
67.(2022·江苏盐城·七年级期末)计算或化简
(1);
(2);
(3);
(4).
68.(2022·江苏泰州·七年级期末)计算
(1)
(2)
69.(2022·江苏南京·七年级期末)先化简,再求值:,其中x=-1,y=.
70.(2022·江苏无锡·七年级期末)定义:若,则称x与y是关于m的相关数.
(1)若5与a是关于2的相关数,则_____.
(2)若A与B是关于m的相关数,,B的值与m无关,求B的值.
71.(2022·江苏扬州·七年级期末)解下列方程:
(1)4x﹣3=2(x﹣1)
(2)
72.(2022·江苏·南京市第二十九中学七年级期末)某超市有线上和线下两种销售方式.与2019年4月份相比.该超市2020年4月份销售总额增长其中线上销售额增长.线下销售额增长,
(1)设2019年4月份的销售总额为元.线上销售额为元,请用含的代数式表示2020年4月份的线下销售额(直接在表格中填写结果);
时间.
销售总额(元)
线上销售额(元)
线下销售额(元)
2019年4月份
a
x
a- x
2020年4月份
1.1a
1.43x
(2)求2020年4月份线上销售额与当月销售总额的比值.
73.(2022·江苏扬州·七年级期末)解方程
(1) (2)
74.(2022·江苏南京·七年级期末)如图1,线段.
(图1)
(1)点沿线段自点向点以厘米/秒运动,同时点沿线段自点向点以厘米/秒运动,几秒钟后、两点相遇?
(2)如图2,,,现点绕着点以的速度顺时针旋转一周后停止,同时点沿直线自点向点运动,假若点、两点也能相遇,求点运动的速度.
(图2)
75.(2022·江苏盐城·七年级期末)某校为承办县初中学校内涵建设,需制作一块活动展板,请来师徒两名工人.已知师傅单独完成需4天,徒弟单独完成需6天.
(1)两个人合作需要多少天完成?
(2)现由徒弟先做1天,师徒两人再合作完成这项工作,问:徒弟共做了几天?
76.(2022·江苏盐城·七年级期末)已知A=3x2+2x﹣1,B=﹣2x2﹣3x+5.求:
(1)A﹣2B;
(2)若2A与3B互为相反数,求x的值.
77.(2022·江苏扬州·七年级期末)解方程:
(1); (2).
78.(2022·江苏南京·七年级期末)如图是由一些大小相同的小正方体组合成的简单几何体.
(1)画出该几何体的主视图和左视图;
(2)如果在这个几何体上再添加一些相同的小正方体,并保持俯视图和左视图不变,那么最多可以再添加 块小正方体.
79.(2022·江苏扬州·七年级期末)一个零件的主视图、左视图、俯视图如图所示(尺寸单位:厘米).
(1)写出这个几何体的名称: ;
(2)根据图中数据计算这个几何体的体积和表面积.
80.(2022·江苏泰州·七年级期末)图①是一个的简单几何体.请在图②的4×4方格纸中分别画出它的主视图、左视图和俯视图(请将所画线加粗).
81.(2022·江苏南京·七年级期末)如图,一个边长为10 cm的无盖正方体可以展开成下面的平面图形.
(1)这个表面展开图的面积是 cm2;
(2)你还能在下面小方格中画出无盖正方体的其他不同形状的表面展开图吗?请画出所有可能的情形(把需要的小正方形涂上阴影);
(3)将一个无盖正方体展开成平面图形的过程中,需要剪开 条棱.
A.3 B.4 C.5 D.不确定
82.(2022·江苏南京·七年级期末)在平整的地面上,由若干个完全相同的棱长为的小正方体堆成一个几何体,如图所示.
(1)请你在方格纸中分别画出这个几何体的主视图和左视图;
(2)若现在手头还有一些相同的小正方体,如果保持这个几何体的主视图和俯视图不变,
Ⅰ.在图中所示几何体上最多可以添加______个小正方体;
Ⅱ.在图中所示几何体上最多可以拿走______个小正方体;
83.(2022·江苏无锡·七年级期末)如图由若干个相同的小立方体搭成的一个几何体的主视图和俯视图,俯视图的方格中的字母和数字表示该位置上小立方体的个数.
(1)填空:x= ,y= ;
(2)利用上题结论,先化简再求值:2(3x2y﹣xy2)﹣(xy2+4x2y)+2xy2.
84.(2022·江苏·射阳县第六中学七年级期末)如图,是由若干个完全相同的小正方体组成的一个几何体.
(1)请在网格中画出几何体的主视图、左视图、俯视图;
(2)图中共有 个小正方体.
(3)已知每个小正方体的棱长为1cm,则该几何体的表面积为 cm2.
85.(2022·江苏徐州·七年级期末)如图是用6个棱长为1cm的正方体搭成的几何体.
(1)在所给方格纸中,用实线画出它的三个视图;
(2)该几何体的表面积(含底部)为 cm2.
86.(2022·江苏淮安·七年级期末)如图是小明用10块棱长都为1cm的正方体搭成的几何体.
(1)分别画出从正面、从左面、从上面看到的所搭几何体的形状图并涂阴影;
(2)小明所搭几何体的表面积(包括与桌面接触的部分)是 .
87.(2022·江苏江苏·七年级期末)如图,是由几个大小完全相同的小正方体垒成的几何体.
(1)图中共有 个小正方体;
(2)请分别画出你所看到的几何体的三视图(请用黑水笔描清楚).
88.(2022·江苏南京·七年级期末)如图,∠AOB=100°,OC、OD是两条射线,射线OD平分∠BOC,∠BOD=20°.
(1)图中共有 个角;
(2)求∠AOC的度数;
(3)作射线OE.若∠BOE=50°,则∠DOE的度数为 °.
89.(2022·江苏扬州·七年级期末)补全下面的解题过程:
如图,已知OC是∠AOB内部的一条射线,OD是∠AOB的平分线,∠AOC=2∠BOC,且∠BOC=40°,求∠COD的度数.
解:∵∠AOC=2∠BOC,∠BOC=40°,
∴∠AOC= °.
∴∠AOB=∠AOC+∠ = °.
∵OD平分∠AOB,
∴∠AOD=∠AOB= °.
∴∠COD=∠ ﹣∠AOD=20°.
90.(2022·江苏南京·七年级期末)读句画图.
(1)画射线,连接并延长线段至;
(2)用直尺和圆规作,使得.
91.(2022·江苏淮安·七年级期末)如图,C为线段AD上一点,B为CD的中点,AD=20cm,AC=12cm.
(1)图中共有 条线段;
(2)求BD的长;
(3)若点E在线段BD上,且BE=3cm,求AE的长.
92.(2022·江苏淮安·七年级期末)如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=25°,求∠COD的度数.
93.(2022·江苏淮安·七年级期末)在如图所示的方格纸中,每个小正方形的顶点称为格点,每个小正方形的边长为1,已知四边形ABCD的四个顶点在格点上,利用格点和直尺按下列要求画图:
(1)过点C画AD的平行线CE;
(2)过点B画CD的垂线,垂足为F.
(3)线段CF表示点 到线段 的距离.
94.(2022·江苏泰州·七年级期末)如图,已知,,点D为线段AC的中点,分别求线段CD、BC的长度.
95.(2022·江苏盐城·七年级期末)如图,点O在直线AB上,CO⊥AB,∠2﹣∠1=34°,OE是∠AOD的平分线,OF⊥OE.
(1)求∠AOE的度数.
(2)找出图中与∠BOF互补的角,并求出∠BOF补角的度数.
96.(2022·江苏宿迁·七年级期末)如图,已知∠AOB=30°,完成下列问题:
(1)在射线OB上取一点C,使OC=2cm;
(2)过点C画直线m,使m//OA;
(3)过点O画直线l,使l⊥OA;
(4)设直线m与直线l交于点D,度量线段OD= cm,∠OCD= 度.
97.(2022·江苏宿迁·七年级期末)如图,,,,求的度数.
98.(2022·江苏宿迁·七年级期末)在图中“〇”内添上字母A、B、C,使AC<AB<BC.
99.(2022·江苏盐城·七年级期末)如图,平面上有三个点A、B、C.
(1)根据下列语句按要求画图.
①画射线AB,用圆规在线段AB的延长线上截取BD=AB(保留作图痕迹),连接CA、CD、CB;
②过点C画CE⊥AD,垂足为点E;
③过点D画DF//AC,交CB的延长线于点F.
(2)①在线段CA、CE、CD中,线段______最短,依据是______.
②用刻度尺或圆规检验线段DF与AC的关系为______.
100.(2022·江苏盐城·七年级期末)已知:如图,A、B、C三点在同一条直线上,BC=3AB,D为AC中点,E为BC中点.若线段AC的长为8,求线段DE的长.
答案与解析
一、单选题
1.(2022·江苏泰州·七年级期末)下列所给数据中,能反映出一瓶矿泉水重量的是( ).
A.500毫克 B.500克 C.500千克 D.500吨
【答案】B
【分析】根据生活常识,即可得到一瓶矿泉水重量.
【详解】解:能反映出一瓶矿泉水重量的是500克.
故选:B.
【点睛】本题考查了数学常识,是基础题型,比较简单.
2.(2022·江苏淮安·七年级期末)下列四个数中,无理数是( )
A. B.π C.0.12 D.0
【答案】B
【分析】利用无理数的定义进行判断即可.
【详解】解:根据无理数的定义可知无理数是无限不循环小数,
∴π为无理数,
故选:B.
【点睛】本题主要考查的是无理数的定义,注意分数,有限小数,无限循环小数都属于有理数.
3.(2022·江苏盐城·七年级期末)的倒数是( )
A. B. C. D.
【答案】B
【分析】根据倒数的定义:乘积为1的两个数互为倒数,即可得出答案.
【详解】解:因为,
所以的倒数是,
故选:B.
【点睛】本题考查了倒数,掌握乘积为的两个数互为倒数是解题的关键.
4.(2022·江苏宿迁·七年级期末)能说明命题“任何数a的平方都大于0.”是假命题的一个反例可以是( )
A. B. C. D.
【答案】B
【分析】a的平方大于等于0,因此找出a的平方等于0的选项即可.
【详解】解:当时,a的平方等于0,
因此能说明命题“任何数a的平方都大于0”是假命题,
故选B.
【点睛】本题考查举反例,掌握“a的平方大于等于0”是解题的关键.
5.(2022·江苏镇江·七年级期末)下列计算正确的是( )
A.﹣2+3=5 B.﹣7﹣(﹣4)=﹣3
C. D.(﹣)÷(﹣8)=1
【答案】B
【分析】根据有理数的运算法则逐项计算即可.
【详解】解:A、﹣2+3=1,故选项A错误,不符合题意;
B、﹣7﹣(﹣4)=﹣7+4=﹣3,故选项B正确,符合题意;
C、,故选项C错误,不符合题意;
D、(﹣)÷(﹣8)=,故选项D错误,不符合题意;
故选:B.
【点睛】本题考查了有理数的相关运算,熟练掌握运算法则是解题的关键.
6.(2022·江苏南通·七年级期末)规定:表示向右移动2,记作+2,则表示向左移动5,记作( )
A.+5 B.-5 C. D.-
【答案】B
【分析】根据题意,在表示相反意义的量中,规定其中一个为正,则另一个为负,即可得出答案.
【详解】解:因为表示向右移动2,记作+2,
∴则表示向左移动5,记作-5;
故选B
【点睛】本题考查正负数的概念,解题的关键在于理解相反意义的量.
7.(2022·江苏扬州·七年级期末)当前手机移动支付已经成为新型的支付方式,图中是妈妈元旦当天的微信零钱支付明细,则妈妈元旦当天的微信零钱收支情况是( )
转账﹣来自SNM
+48
云视听极光
﹣30
扫二维码付款
﹣50
A.收入128元 B.收入32元 C.支出128元 D.支出32元
【答案】D
【分析】根据正数和负数表示相反意义的量,可得答案.
【详解】解:+48﹣30﹣50=﹣32,
所以妈妈元旦当天的微信零钱收支情况是支出32元.
故选:D.
【点睛】本题考查了正数和负数以及有理数的加减法,确定相反意义的量是解题关键.
8.(2022·江苏苏州·七年级期末)下列计算正确的是( )
A. B. C. D.
【答案】D
【分析】根据合并同类项的计算法则求解判断即可.
【详解】解:A、与不是同类项,不能合并,计算错误,不符合题意;
B、,计算错误,不符合题意;
C、,计算错误,不符合题意;
D、,计算正确,符合题意;
故选D.
【点睛】本题主要考查了合并同类项,熟知合并同类项的计算法则是解题的关键.
9.(2022·江苏无锡·七年级期末)下列计算正确的是( )
A. B.
C. D.
【答案】C
【分析】根据合并同类项法则逐项判断即可得.
【详解】解:A、与不是同类项,不可合并,则此项错误,不符题意;
B、与不是同类项,不可合并,则此项错误,不符题意;
C、,则此项正确,符合题意;
D、与不是同类项,不可合并,则此项错误,不符题意;
故选:C.
【点睛】本题考查了合并同类项,熟练掌握合并同类项法则是解题关键.
10.(2022·江苏南通·七年级期末)计算﹣(4a﹣5b),结果是( )
A.-4a-5b B.-4a+5b C.4a-5b D.4a+5b
【答案】B
【分析】根据去括号法则:括号前是负号,去掉括号和负号,括号内各项要变号,即可得答案.
【详解】解:,
故选:B.
【点睛】本题考查去括号,解题的关键是掌握去括号法则:括号前是负号,去掉括号和负号,括号内各项要变号.
11.(2022·江苏南通·七年级期末)若与是同类项,则的值为( )
A.-1 B.-5 C.5 D.7
【答案】D
【分析】根据同类项是字母相同且相同字母的指数也相同,可得答案.
【详解】解:与是同类项,
,,
.
故选:D.
【点睛】本题考查了同类项,利用相同且相同字母的指数也相同得出方程是解题关键.
12.(2022·江苏南京·七年级期末)是下面哪个二元一次方程的解( )
A. B. C. D.
【答案】D
【分析】把解代入各个选项中,满足方程成立的符合条件.
【详解】解:把x=5代入A,得y=5+2=3,所以不是二元一次方程A的解,不符合题意;
把x=5代入B,得y=(51)÷2=2,所以不是二元一次方程B的解,不符合题意;
把x=5代入C,得y=5+2=7,所以不是二元一次方程C的解,不符合题意;
把x=5代入D,得y=(101)÷3=3,所以是二元一次方程D的解,符合题意.
故选:D.
【点睛】本题考查了方程解的定义,掌握二元一次方程解的定义是解决本题的关键.
13.(2022·江苏无锡·七年级期末)下列方程为一元一次方程的是( )
A. B. C. D.
【答案】C
【分析】根据一元一次方程的定义逐项判断即可.
【详解】解:A.3x+2y=1中含有两个未知数,所以不是一元一次方程,故本选项不符合题意;
B.x2=1中的未知数的次数是2,所以不是一元一次方程,故本选项不符合题意;
C.x-1=0符合一元一次方程的定义,故本选项符合题意;
D.y=x-1中含有两个未知数,所以不是一元一次方程,故本选项不符合题意.
故选:C.
【点睛】本题考查了一元一次方程的定义,注意:只含有一个未知数,并且所含未知数的项的最高次数是1次的整式方程,叫一元一次方程.
14.(2022·江苏南京·七年级期末)将如图所示的长方形绕它的对角线所在直线旋转一周,形成的几何体是( )
A. B. C. D.
【答案】B
【分析】根据矩形角度和顶点观察,绕对角线可得答案.
【详解】解:通过观察可知,B图形的构造满足旋转结果.
故选:B.
【点睛】本题主要考查旋转的性质,认真观察旋转中心和线段、角度的特点是解题的关键.
15.(2022·江苏无锡·七年级期末)如图是一个小正方体的表面展开图,把展开图折叠成小正方体后,有“开”字一面的相对面上的字是( )
A.我 B.爱 C.教 D.育
【答案】B
【分析】根据正方体的表面展开图找相对面的方法,同层隔一面来判断即可;也可用纸按图的样子折叠后得出结论.
【详解】解:有“开”字一面的相对面上的字是:爱,
故选:B.
【点睛】本题考查了正方体相对两个面上的文字问题;熟练掌握根据正方体的表面展开图找相对面的方法是解题的关键.解答此类问题关键是需要从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立方体图形与平面图形的转化,建立空间观念.
16.(2022·江苏宿迁·七年级期末)如图,下列几何体中,主视图和俯视图相同的是( )
A. B.
C. D.
【答案】C
【分析】分别分析四种几何体的主视图和左视图,找出主视图和左视图相同的几何体即可.
【详解】A.主视图是长方形,俯视图是圆形,不符合题意;
B.主视图是两个拼在一起的长方形,俯视图是三角形,不合题意;
C.主视图和俯视图都是是正方形,符合题意;
D.主视图是两个拼在一起的三角形,俯视图是三个拼在一起三角形,不合题意;
故选:C.
【点睛】本题考查了简单几何体的三视图,解决问题的关键是掌握主视图是从物体的正面看到的视图,左视图是从物体的左面看得到的视图.
17.(2022·江苏宿迁·七年级期末)某正方体的每一个面上都有一个汉字,如图是它的种表面展开图,那么在原正方体的表面上,与“洗”字相对的面上的汉字是( )
A.罩 B.勤 C.口 D.戴
【答案】D
【分析】根据正方体的表面展开图,相对的面之间一定相隔一个正方形,即可求解.
【详解】解:根据题意得:“勤”与“罩”是相对面,
“洗”与“戴”是相对面,
“手”与“口”是相对面.
故选:D.
【点睛】本题主要考查了正方体相对两个面上的文字,熟练掌握正方体的表面展开图,相对的面之间一定相隔一个正方形是解题的关键.
18.(2022·江苏南京·七年级期末)如图是一个几何体的侧面展开图,则该几何体是( )
A.三棱柱 B.三棱锥 C.五棱柱 D.五棱锥
【答案】D
【分析】由题意可知,该几何体侧面为5个三角形,底面是五边形,从而得到该几何体为五棱锥,即可求解.
【详解】解:由题意可知,该几何体侧面为5个三角形,底面是五边形,
所以该几何体为五棱锥.
故选:D
【点睛】本题主要考查了几何体的展开图,熟练掌握棱锥的展开图是解答本题的关键.
19.(2022·江苏南通·七年级期末)如图,分别从正面、左面、上面观察圆柱,得到的平面图形分别是( )
A. B.
C. D.
【答案】A
【分析】根据从物体正面、左面和上面看,所得到的图形即可得解.
【详解】解:圆柱体从正面、左面看到的平面图形都是一个长方形,从上面看到的平面图形是一个圆.
故选:A.
【点睛】本题考查了从不同方向看几何体,考查了学生的思考能力和对几何体三种视图的空间想象能力和综合能力.
20.(2022·江苏无锡·七年级期末)如图,C、D是线段AB上两点,且,则AC与BD的关系是( )
A. B. C. D.
【答案】C
【分析】先分别表示出AC和BD,即可求出两者的关系.
【详解】解:∵AC=AD-CD=AD-3AD+2BC=2BC-2AD=2(BC-AD),
BD=BC-CD=BC-3AD+2BC=3BC-3AD=3(BC-AD),
∴,
∴3AC=2BD,
故选:C.
【点睛】本题考查线段的计算,熟练掌握线段的和差是解题的关键.
21.(2022·江苏无锡·七年级期末)若∠1与∠2互余,∠1与∠3互补,则∠2与∠3的关系是( )
A. B. C. D.
【答案】B
【分析】根据若两角的和为90°,则两角互余;若两角的和为180°,则两角互补,解答即可.
【详解】∵∠1和∠2互余,∠1与∠3互补,
∴∠1+∠2=90°,∠1+∠3=180°,
∴∠1=90°-∠2=180°-∠3,
∴∠3-∠2=90°.
故选: B.
【点睛】本题主要考查了互为余角和互为补角的定义,若两角的和为90°,则两角互余;若两角的和为180°,则两角互补.
22.(2022·江苏常州·七年级期末)如图,已知A、B、C三点,过点A可画直线BC的平行线的条数是( )
A.0条 B.1条 C.2条 D.无数条
【答案】B
【分析】先过B,C两点画直线BC,再根据过直线外一点有且只有1条直线与已知直线平行可求解.
【详解】解:如图,
根据过直线外一点有且只有1条直线与已知直线平行,
故选:B.
【点睛】本题主要考查直线,射线,线段,平行线,掌握过直线外一点有且只有1条直线与已知直线平行的性质是解题的关键.
23.(2022·江苏南京·七年级期末)如图,,,垂足分别为C、D,线段的长度是( )
A.点A到的距离 B.点B到的距离
C.点C到的距离 D.点D到的距离
【答案】C
【分析】根据点到直线的距离等于垂线段的长度即可求解.
【详解】解:依题意,,,
点A到的距离是线段的长度,
点B到的距离是线段的长度,
点C到的距离是线段的长度
点D到的距离图中没有标出,
故选C
【点睛】本题考查了点到直线的距离的定义,数形结合以及理解定义是解题的关键.点到直线的距离的等于垂线段的长度.
24.(2022·江苏盐城·七年级期末)要在墙上固定一根木条,小明说只需要两根钉子,这其中用到的数学道理是( )
A.两点之间线段最短 B.两点确定一条直线
C.垂线段最短 D.两条直线相交,只有一个交点
【答案】B
【分析】根据两个钉子固定一根木条可知两点确定一条直线.
【详解】解:由题意知,用到的数学道理是两点确定一条直线
故选B.
【点睛】本题考查了两点确定一条直线的应用.解题的关键在于掌握两点确定一条直线的含义与应用.
25.(2022·江苏无锡·七年级期末)下列人或物中,质量最接近1吨的是( )
A.1000枚1元硬币 B.25名小学生
C.5000个鸡蛋 D.10辆家用轿车
【答案】B
【分析】质量单位有:吨、千克、克,本题中结合实际情况选择合适的计量单位即可判断出答案.例如:1名六年级的学生大约重40kg,求出25名学生的重量;1个鸡蛋大约50g,求出5000个鸡蛋的重量等等.
【详解】解:1吨=1000千克,
A、1元硬币1个大约6 g,1000×6 g=6000 g=6kg,故此选项不符合题意;
B、六年级的学生体重大约40kg,25×40kg=1000kg,故此选项符合题意;
C、1个鸡蛋大约50g,5000×50g=250000g=250kg,故此选项不符合题意;
D、1辆家用轿车大约1500kg,10×1500kg=15000kg,故此选项不符合题意.
故选:B.
【点睛】本题考查了根据情景选择合适的计量单位,联系生活实际、计量单位,算出这些数据的大小再选择是解题的关键.
26.(2022·江苏扬州·七年级期末)的相反数是( )
A. B. C. D.
【答案】D
【分析】根据相反数的定义即可求解.相反数的定义是:如果两个数只有符号不同,我们称其中一个数为另一个数的相反数,特别地,0的相反数还是0.
【详解】解:的相反数是,
故选D.
【点睛】本题考查了相反数,掌握相反数的定义是解题的关键.
27.(2022·江苏扬州·七年级期末)下列代数式的值一定是正数的是( )
A. B. C. D.
【答案】D
【分析】根据正负数、非负数的性质,绝对值的性质,逐项判断即可求解.
【详解】解:A、当时,,故本选项不符合题意;
B、当时,,故本选项不符合题意;
C、,故本选项不符合题意;
D、,一定是正数,故本选项符合题意;
故选:D.
【点睛】本题主要考查了正负数、非负数的性质,绝对值的性质,熟练掌握正负数的判断方法及非负数的性质的正确应用是解题关键.
28.(2022·江苏南京·七年级期末)据统计,电影《长津湖》上映第16天,累计票房突破45.6亿元.将数据45.6亿用科学记数法表示为( )
A.45.6×108 B.4.56×109 C.4.56×1010 D.0.456×1011
【答案】B
【分析】用科学计数法表示较大的数时,一般形式为,其中,n为整数,且n比原来的整数位数少1,据此判断即可.
【详解】解:45.6亿=4560000000=4.56×109,
故选:B.
【点睛】此题考查了用科学计数法表示较大的数时,一般形式为,其中,确定a与n的值是解题关键.
29.(2022·江苏扬州·七年级期末)已知a,b的位置如图,则的值为( )
A.0 B.-2b C.-2a D.2b-2a
【答案】B
【分析】结合数轴可知:,进一步可知:,,再去绝对值即可.
【详解】解:由图可知:,
∴,,
∴.
故选:B
【点睛】本题考查根据数轴上的点判断式子的正负,去绝对值,解题的关键是根据数轴得出,得出,.
二、填空题
30.(2022·江苏宿迁·七年级期末)某种细菌病毒的直径为0.000000505米,0.000000505米用科学记数法表示为____米.
【答案】
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】解:.
故答案为:.
【点睛】本题考查用科学记数法表示较小的数,一般形式为,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
31.(2022·江苏扬州·七年级期末)天宫二号是中国首个具备补加功能的载人航天科学实验空间实验室,天宫二号的轨道高度约为393000m,393000m用科学记数法表示为 _____m.
【答案】3.93×105
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【详解】解:393000m=3.93×105m.
故答案是:3.93×105.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
32.(2022·江苏扬州·七年级期末)单项式的系数是_____.
【答案】
【分析】根据单项式的系数的定义,即可求解.
【详解】解:单项式的系数是.
故答案为:.
【点睛】本题主要考查了单项式的系数和次数的定义,熟练掌握单项式中的数字因式是单项式的系数,所有字母的次数之和是单项式的次数是解题的关键.
33.(2022·江苏南通·七年级期末)有一个两位数,个位数字是n,十位数字是m,则这个两位数可表示为__________.
【答案】10m+n##n+10m
【分析】根据一个两位数,个位数字是n,十位数字是m,可以用含m、n的代数式表示出这个两位数.
【详解】解:由题意可得,
这个两位数为:10m+n,
故答案为:10m+n.
【点睛】本题考查列代数式,解答本题的关键是明确题意,列出相应的代数式.
34.(2022·江苏扬州·七年级期末)单项式的系数是____.
【答案】
【分析】单项式的系数就是所含字母前面的因数,由此即可求解.
【详解】解: 单项式的系数是.
故答案为:
【点睛】本题考查单项式的系数的定义,解题关键是熟练掌握相关的定义即可求解.
35.(2022·江苏扬州·七年级期末)若a,b互为倒数,则﹣4ab+1的值为______.
【答案】﹣3
【分析】根据倒数的概念可得ab=1,再代入计算可求解.
【详解】解:∵a,b互为倒数,
∴ab=1,
∴﹣4ab+1=﹣4+1=﹣3,
故答案为:﹣3.
【点睛】本题主要考查倒数,代数式求值,利用倒数的定义求解ab的值是解题的关键.
36.(2022·江苏宿迁·七年级期末)已知方程的解是,则k的值为 _____.
【答案】5
【分析】根据方程解的定义把代入方程可得到关于k的新的一元一次方程,通过解新方程即可求得k的值.
【详解】解:把代入方程可得:
解得.
故答案是:5
【点睛】本题考查了一元一次方程的解的定义:使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解.把方程的解代入方程得到k的一元一次方程是解题的关键.
37.(2022·江苏扬州·七年级期末)当x=____时,代数式=4.
【答案】5
【分析】去分母、移项、合并同类项、系数化为1,据此求出方程的解即可.
【详解】解:去分母,可得:,
移项,可得:,
合并同类项,可得:,
系数化为1,可得,
当时,代数式.
故答案为:5.
【点睛】此题主要考查了解一元一次方程的方法,要熟练掌握解一元一次方程的一 般步骤:去分母、去括号、移项、合并同类项、系数化为1.
38.(2022·江苏南京·七年级期末)已知x=-1是方程2ax-5=a-2的解,则a=______.
【答案】-1
【分析】把x=-1代入方程2ax-5=a-2,化简求值即可.
【详解】解:∵x=-1是方程2ax-5=a-2的解,
∴,解得.
故答案为:.
【点睛】本题主要考查一元一次方程的解法,熟练掌握计算步骤是解题的关键.
39.(2022·江苏南京·七年级期末)写出一个解是,未知数的系数为3,且等号左边为多项式的一元一次方程_______.
【答案】(答案不唯一)
【分析】根据题目的要求和一元一次方程的定义即可解答.
【详解】解:根据题意可得,(答案不唯一),
故答案为:(答案不唯一)
【点睛】本题考查了一元一次方程的定义,熟记定义是解题的关键.
40.(2022·江苏南京·七年级期末)三视图都是圆形的几何体是______.
【答案】球
【分析】根据三视图的定义求解即可.
【详解】解:由题意得,球的三视图都是圆,
故答案为:球.
【点睛】本题主要考查了简单几何体的三视图,熟知三视图的定义是解题的关键.
41.(2022·江苏常州·七年级期末)如图所示是一个几何体的三视图,若这个几何体的体积是6,则它的表面积是________.
【答案】22
【分析】根据主视图与左视图得出长方体的边长,再利用图形的体积得出它的高,进而得出表面积.
【详解】由主视图得出长方体的长是3,宽是1,这个几何体的体积是6,
设高为h,则3×1×h=6,
解得: h=2,
它的表面积是:
2×3×2+2×3×1+2×1×2
=22.
故答案为:22.
【点睛】此题主要考查了利用三视图判断几何体的边长,得出图形的高是解题关键.
42.(2022·江苏南京·七年级期末)如图是一个正方体的表面展开图,每个面上都标有字母.其中与字母A处于正方体相对面上的是字母_______.
【答案】F
【分析】根据正方体的表面展开图找相对面的方法,“Z”字两端是对面判断即可.
【详解】解:与字母A处于正方体相对面上的是字母:F,
故答案为:F.
【点睛】本题考查了正方体相对两个面上的文字,熟练掌握根据正方体的表面展开图找相对面的方法是解题的关键.
43.(2022·江苏淮安·七年级期末)如图,将一副三角板叠在一起,使它们的直角顶点O重合,若∠AOB=165°,则∠COD的度数为____.
【答案】15°##15度
【分析】先根据直角三角板的性质得出∠AOD+∠COB=180°,进而可得出∠COD的度数.
【详解】解:∵△AOD与△BOC是一副直角三角板,
∴∠AOD+∠COB=180°,
∴∠AOC+2∠COD+∠BOD=∠AOB+∠COD=180°.
∵∠AOB=165°,
∴∠COD=180°﹣∠AOB=180°﹣165°=15°.
故答案为15°.
【点睛】本题考查了角度的计算,熟知直角三角板的特点,找准各角之间的关系是解答此题的关键.
44.(2022·江苏常州·七年级期末)如图,∠1=133°25′,AO⊥OB于点O,点C、O、D在一条直线上,则∠2的度数等于______.
【答案】43°25′
【分析】根据平角定义先求出∠AOD的度数,再根据垂直定义求出∠AOB=90°,从而求出∠2的度数.
【详解】解:∵∠1=133°25′,
∴∠AOD=180°-∠1=46°35′,
∵AO⊥OB,
∴∠AOB=90°,
∴∠2=∠AOB-∠AOD=43°25′,
故答案为:43°25′.
【点睛】本题考查了垂线,度分秒的换算,根据题目的已知条件并结合图形分析是解题的关键.
45.(2022·江苏盐城·七年级期末)北京时间20点30分,此时钟表的时针和分针构成的角度是 _____°.
【答案】75
【分析】用时针与分针相距的大格数乘以每大格的度数,可得答案.
【详解】解:20点30分就是晚上8点30分.
8点30分,时钟的时针和分针相距2大格.
8点30分,时钟的时针和分针所构成的锐角度数为.
故答案为:75.
【点睛】本题考查钟面角的计算,熟练掌握该知识点是解题关键.
46.(2022·江苏盐城·七年级期末)下列生产和生活现象:①把弯曲的公路改直,就能缩短路程;②用两个钉子就可以把木条固定在墙上;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;④从A地到B地架设电线,总是尽可能沿着线段AB架设.其中能用“两点确定一条直线”来解释的现象有 _____.(填序号)
【答案】②③
【分析】根据两点确定一条直线,两点之间线段最短的性质对各选项分析判断后利用排除法求解.
【详解】解:①把弯曲的公路改直,就能缩短路程是利用了“两点之间,线段最短”,故此项不符合;
②用两个钉子就可以把木条固定在墙上是利用了“两点确定一条直线”,故此项符合;
③植树时,只要定出两棵树的位置,就能确定同一行树所在的直线是利用了“两点确定一条直线”,故此项符合;
④从A地到B地架设电线,总是尽可能沿着线段AB架设.是利用了“两点之间,线段最短”,故此项不符合.
故答案为:②③.
【点睛】本题考查了线段的性质以及直线的性质,熟记性质公理是解题的关键.
47.(2022·江苏宿迁·七年级期末)已知与互为补角,且,则_____.
【答案】
【分析】根据“和为的两个角互为补角”,用即可.
【详解】解:根据题意可知,
,
∵,
∴,
故答案为:.
【点睛】本题考查补角的定义,角度之间的计算,解题的关键是理解补角的定义.
48.(2022·江苏泰州·七年级期末)如图,OA表示北偏东20°方向的一条射线,OB表示南偏西50°方向的一条射线,则的度数是_____________.
【答案】150°
【分析】根据方向角的定义可直接确定∠AOB的度数.
【详解】∵OA表示北偏东20°方向的一条射线,OB表示南偏西50°方向的一条射线,
∴∠AOB=20°+90°+(90°-50°)=150°.
故答案为:150°.
【点睛】本题考查了方向角及其计算.掌握方向角的概念是解题的关键.
49.(2022·江苏泰州·七年级期末)若,则的余角的度数是___________.
【答案】43°##43度
【分析】根据互余两角之和等于90°即可得出答案.
【详解】∵∠α =47°,
∴∠α 的余角=90°-∠α =90°-47°=43°.
故答案为:43°.
【点睛】本题考查了余角的知识,属于基础题,解答本题的关键是熟记互余两角之和等于90°.
50.(2022·江苏宿迁·七年级期末)如图,在直线l上有A,B,C三点,则图中的线段共有 _____条.
【答案】3
【分析】根据线段定义(指直线上两点间的有限部分(包括两个端点)),找出图中的线段,即可得答案.
【详解】解:图中的线段有:线段AB,线段BC,线段AC,共3条,
故答案为:3.
【点睛】本题考查线段的定义,熟记线段的定义及数线段方法是解题关键.
51.(2022·江苏无锡·七年级期末)已知∠α=96°24′,则∠α的补角为______.
【答案】83°36′
【分析】根据“和为180°的两个角互为补角”,用180°-∠α即可.
【详解】解:∵∠α=96°24′,
∴∠α的补角为:180°-∠α=180°-96°24′=83°36′,
故答案为:83°36′.
【点睛】本题主要考查补角的定义,度分秒的换算,关键是区分清楚余角和补角的定义.“和为180°的两个角互为补角”,“和为90°的两个角互为余角”.
52.(2022·江苏·射阳县第六中学七年级期末)如图,想在河堤两岸搭建一座桥,搭建方式最短的是线段 _____.
【答案】PN
【分析】根据从直线外一点到这条直线上各点所连的线段中,垂线段最短可知搭建方式最短的是PN,理由垂线段最短.
【详解】解:因为PN⊥MQ,垂足为N,则PN为垂线段,
根据垂线段最短,可得线段PN最短,
故答案为:PN.
【点睛】本题考查了垂线段最短,利用垂线段的性质是解题关键.
53.(2022·江苏南京·七年级期末)比较大小:-______-,(填“>”、“<”或“=”)
【答案】>
【分析】根据“两个负数比较大小,绝对值大的反而小”进行比较.
【详解】∵,,
∴,
∴,
∴.
故答案为:>
【点睛】本题主要考查了有理数大小的比较,熟练掌“握两个负数比较大小,绝对值大的反而小”是解题的关键.
54.(2022·江苏淮安·七年级期末)如图是一个数值运算程序,当输入的值为﹣2时,则输出的的值为 _____.
【答案】-18
【分析】把x=﹣2代入运算程序求值即可得最后结果.
【详解】解:把x=﹣2代入得,
(﹣2)2×(﹣5)+2
=4×(﹣5)+2
=﹣20+2
=﹣18,
故答案为:﹣18.
【点睛】本题考查了代数式求值,有理数的混合运算,掌握运算程序的意义,读懂题意是解题关键.
三、解答题
55.(2022·江苏无锡·七年级期末)计算:
(1);
(2).
【答案】(1)
(2)8
【分析】(1)先算绝对值,再算有理数的乘法,再算加减即可.
(2)先算乘方,有理数的除法,再算加减即可.
(1)
解:
(2)
解:
【点睛】本题考查了有理数的混合运算,解答本题的关键是明确有理数混合运算的运算法则和运算顺序.
56.(2022·江苏盐城·七年级期末)计算:
(1)
(2)
【答案】(1)15
(2)0
【分析】(1)先去括号去绝对值符号,再根据运算顺序,先算乘除再算加减;
(2)先去括号,根据运算顺序,先算乘方再算乘除再算加减;
(1)
解:原式=8-5+43
=8-5+12
=15
(2)
解:原式=-1+
=-1+1
=0
【点睛】本题考查了有理数的混合运算,解题的关键是熟练掌握绝对值、乘方以及乘法的分配律,有理数相乘的时候可以根据同号正异号负的原则先确定符号再运算绝对值.
57.(2022·江苏淮安·七年级期末)计算:
(1)2×(﹣2)+3
(2)
【答案】(1)-1 ;
(2)7
【解析】(1)
解:2×(﹣2)+3
=-4+3
=-1
(2)
解:
【点睛】此题主要考查了有理数的混合运算,熟悉运算法则是解题关键.
58.(2022·江苏泰州·七年级期末)计算:
(1);
(2).
【答案】(1)
(2)4
【解析】(1)
解:
(2)
解:
【点睛】本题考查了有理数的混合运算,解题的关键是掌握运算法则和运算顺序.
59.(2022·江苏盐城·七年级期末)解下列方程:
(1);
(2).
【答案】(1);(2)
【分析】(1)方程去括号、移项、合并同类项、系数化为1即可;
(2)方程去分母、去括号、移项、合并同类项、系数化为1即可.
【详解】(1)解:
去括号,得.
移项,得.
合并同类项,得.
系数化为1,得.
(2)解:
去分母,得.
去括号,得.
移项,得.
合并同类项,得.
系数化为1,得.
【点睛】本题考查了解一元一次方程,明确解方程的先后顺序是解决问题的关键.
60.(2022·江苏南京·七年级期末)如图,是一个由7个正方体组成的立体图形.画出该立体图形的主视图、左视图和俯视图.
【答案】见解析
【分析】根据三视图的定义,画出图形,即可求解.
【详解】解:根据题意得:该立体图形的主视图、左视图和俯视图如下图所示:
【点睛】本题主要考查了几何体的三视图,熟练掌握三视图是观测者从三个不同位置观察同一个几何体,画出的平面图形;(1)主视图:从物体前面向后面正投影得到的投影图,它反映了空间几何体的高度和长度;(2)左视图:从物体左面向右面正投影得到的投影图,它反映了空间几何体的高度和宽度;(3)俯视图:从物体上面向下面正投影得到的投影图,它反应了空间几何体的长度和宽度是解题的关键.
61.(2022·江苏扬州·七年级期末)有以下运算程序,如图所示:
比如,输入数对(2,1),输出W=2.
(1)若输入数对(1,﹣2),则输出W= ;
(2)分别输入数对(m,﹣n)和(﹣n,m),输出的结果分别是,试比较的大小,并说明理由;
(3)设a=|x+2|,b=|x﹣3|,若输入数对(a,b)之后,输出W=26,请直接写出a+2b的值.
【答案】(1)1
(2),理由见解析
(3)68或73
【分析】(1)根据程序框图,代入求值,即可求解;
(2)根据程序框图,先求出,再比较大小,即可求解;
(3)分三种情况讨论:当x≥3时;当x≤-2时;当-2<x<3时,即可求解.
(1)
解:根据题意得:
;
故答案为:1
(2)
解:,理由如下:
当a=m,b=-n时,
,
当a=-n,b= m时,
∴;
(3)
解:当x≥3时,a=x+2,b=x﹣3,
∵W=26,
∴,
解得:x=24,
∴a=26,b=21,
∴a+2b=68;
当x≤-2时,a=-x-2,b=-x+3,
∵W=26,
∴,
解得:x=-23,
∴a=21,b=26,
∴a+2b=73;
当-2<x<3时,a=x+2,b=-x+3,
∴,
即,
解得:x=25或-22,不符合题意,舍去;
综上所述,a+2b的值为68或73.
【点睛】本题主要考查了求代数式的值及含绝对值的一元一次方程,正确表示W是求解本题的关键.
62.(2022·江苏扬州·七年级期末)计算:
(1)
(2)
【答案】(1)3
(2)-3
【分析】(1)先算乘法,再算加减法;
(2)先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
(1)
解:
;
(2)
解:
.
【点睛】本题主要考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
63.(2022·江苏淮安·七年级期末)计算:
(1)﹣(﹣2)+5+|﹣9|;
(2)﹣14﹣8÷(﹣4)×(﹣6+4).
【答案】(1)16
(2)-5
【分析】(1)先算绝对值,再算加法;
(2)先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
(1)
解:﹣(﹣2)+5+|﹣9|
=2+5+9
=16;
(2)
解:﹣14﹣8÷(﹣4)×(﹣6+4)
=﹣1+2×(﹣2)
=﹣1﹣4
=﹣5.
【点睛】本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
64.(2022·江苏镇江·七年级期末)观察下列式子:
①,
②,
③,
……
(1)根据你发现的规律,请写出第个等式________;
(2)根据你发现的规律,请写出第(为正整数)个等式________,并证明你所写出的等式的正确性;
(3)请写出第198个等式:_________.
【答案】(1)
(2),证明见解析
(3)
【分析】(1)根据题目中式子的特点,可以写出第4个等式;
(2)根据题目中式子的特点,可以写出第个等式并加以证明;
(3)利用(2)进行求解即可.
(1)
解:∵①,
②,
③,
……
特点:等式左边是两个连续偶数的积加1,等式右边是两个连续偶数之间的奇数的平方,序号乘以2就是较小的偶数,
∴第4个等式是:.
故答案为:.
(2)
第个等式是:.
证明:∵左边,
右边,
∴左边=右边.
∴等式成立.
(3)
第个等式为:
即:.
故答案为:.
【点睛】本题主要考查数字的变化规律,解答的关键是由所给的等式总结出存在的规律.
65.(2022·江苏盐城·七年级期末)先化简,再求值:2(3ab2﹣a2b+ab)﹣3(2ab2﹣4a2b+ab),其中a=﹣1,b=2.
【答案】10a2b﹣ab;22
【分析】先把整式去括号、合并同类项化简后,再代入计算即可.
【详解】解:2(3ab2﹣a2b+ab)﹣3(2ab2﹣4a2b+ab)
=6ab2﹣2a2b+2ab﹣6ab2+12a2b﹣3ab
=10a2b﹣ab.
当a=﹣1,b=2时,
原式=10a2b﹣ab
=10×(﹣1)2×2﹣(﹣1)×2
=10×1×2﹣(﹣1)×2
=20+2
=22.
【点睛】本题考查整式加减运算的化简求值,熟练掌握该知识点是解题关键.
66.(2022·江苏盐城·七年级期末)先化简,再求值:已知,,若的值为-8,求的值.
【答案】,0
【分析】先去括号,再合并同类项,将原整式化简,然后再将3b﹣a=﹣8代入求解即可.
【详解】解:A-2B=-2
=-
=
当的值为-8时,
原式=
=
=
=
=0
【点睛】此题考查了整式的混合运算,主要考查了整式的加减法、去括号、合并同类项的知识点.注意运算顺序以及符号的处理.
67.(2022·江苏盐城·七年级期末)计算或化简
(1);
(2);
(3);
(4).
【答案】(1)-58
(2)-9
(3)
(4)
【分析】(1)根据有理数混合运算法则进行运算即可;
(2)先根据乘方运算法则和绝对值的意义进行化简,然后再进行计算即可;
(3)根据合并同类项的法则进行运算即可;
(4)根据整式加减的运算法则进行运算即可.
(1)
解:原式=
=-45-28+15
=-73+15
=-58
(2)
解:原式=(-1)+4×(-)+
=(-1)+(-9)+1
=-9
(3)
解:原式=
(4)
解:原式
【点睛】本题主要考查了有理数的混合运算和整式的加减,熟练掌握有理数的混合运算法则和去括号、合并同类项法则是解题的关键.
68.(2022·江苏泰州·七年级期末)计算
(1)
(2)
【答案】(1)-6
(2)
【分析】(1)利用有理数加法的交换律和结合律,即可求解;
(2)先去括号,再合并同类项,即可求解.
(1)
解:
(2)
解:
【点睛】本题考查整式的加减运算以及有理数的加减运算法则,解题的关键是熟练运用整式的加减运算法则、有理数的运算律,本题属于基础题型.
69.(2022·江苏南京·七年级期末)先化简,再求值:,其中x=-1,y=.
【答案】,4
【分析】先去括号,再合并同数项,最后把x、y用对应的数替换得到一个算式,计算出结果即可.
【详解】解:原式
当x=-1,y=时,
原式
=3+1
=4
【点睛】本题考查整式的化简求值.掌握整式加减混合的运算法则,正确计算是解题关键.
70.(2022·江苏无锡·七年级期末)定义:若,则称x与y是关于m的相关数.
(1)若5与a是关于2的相关数,则_____.
(2)若A与B是关于m的相关数,,B的值与m无关,求B的值.
【答案】(1)
(2)B=8
【分析】(1)根据定义列出式子求解即可;
(2)根据新定义求得B,进而根据题意B的值与m无关,令含m项的系数为0即可求解.
【详解】(1)解:∵5与a是关于2的相关数,
∴
解得;
(2)解:∵A与B是关于m的相关数,,
∴
B的值与m无关,
∴n-2=0,得n=2,
.
【点睛】本题考查了新定义运算,整式的加减无关类型,理解新定义是解题的关键.
71.(2022·江苏扬州·七年级期末)解下列方程:
(1)4x﹣3=2(x﹣1)
(2)
【答案】(1)x=;
(2)x=.
【分析】(1)根据解一元一次方程的一般步骤:去括号、移项、合并同类项、系数化为1,解出x;
(2)根据解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1,解出x.
【详解】(1)解:4x﹣3=2(x﹣1),
去括号,得4x﹣3=2x﹣2,
移项,得4x﹣2x=3﹣2,
合并同类项,得2x=1,
把系数化为1,得x=;
(2),
去分母,得3(x﹣1)﹣(5x+2)=6,
去括号,得3x﹣3﹣5x﹣2=6,
移项,得3x﹣5x=6+3+2,
合并同类项,得﹣2x=11,
把系数化为1,得x=.
【点睛】本题考查解一元一次方程,熟练掌握解一元一次方程的一般步骤是解题的关键.
72.(2022·江苏·南京市第二十九中学七年级期末)某超市有线上和线下两种销售方式.与2019年4月份相比.该超市2020年4月份销售总额增长其中线上销售额增长.线下销售额增长,
(1)设2019年4月份的销售总额为元.线上销售额为元,请用含的代数式表示2020年4月份的线下销售额(直接在表格中填写结果);
时间.
销售总额(元)
线上销售额(元)
线下销售额(元)
2019年4月份
a
x
a- x
2020年4月份
1.1a
1.43x
(2)求2020年4月份线上销售额与当月销售总额的比值.
【答案】(1)
(2)0.2
【分析】(1)由线下销售额的增长率,即可用含a,x的代数式表示出2020年4月份的线下销售额;
(2)根据2020年4月份的销售总额=线上销售额+线下销售额,即可得出关于x的一元一次方程,解之即可得出x的值(用含a的代数式表示),再将其代入中即可求出结论.
【详解】(1)∵与2019年4月份相比,该超市2020年4月份线下销售额增长4%,
∴该超市2020年4月份线下销售额为1.04(a-x)元.
故答案为:1.04(a-x).
(2)依题意,得:1.1a=1.43x+1.04(a-x),
解得:,
∴,
答:2020年4月份线上销售额与当月销售总额的比值为0.2.
【点睛】本题考查了一元一次方程的应用以及列代数式,找准等量关系,正确列出一元一次方程是解题的关键.
73.(2022·江苏扬州·七年级期末)解方程
(1)
(2)
【答案】(1)
(2)
【详解】(1)解:
去括号:
移项合并同类项得:
系数化为1得:x=
(2)−=−1
去分母得:3(3x+1)-(5x-3)=−6
去括号得:9x+3−5x+3=−6
移项,合并同类项得:4x=−12
系数化为1得:x=−3
【点睛】本题考查了解一元一次方程,熟练掌握解方程的一般步骤是解题的关键.
74.(2022·江苏南京·七年级期末)如图1,线段.
(图1)
(1)点沿线段自点向点以厘米/秒运动,同时点沿线段自点向点以厘米/秒运动,几秒钟后、两点相遇?
(2)如图2,,,现点绕着点以的速度顺时针旋转一周后停止,同时点沿直线自点向点运动,假若点、两点也能相遇,求点运动的速度.
(图2)
【答案】(1)4s
(2)或
【分析】(1)根据相遇时,点P和点Q的运动的路程和等于AB的长列方程即可求解;
(2)由于点P,Q只能在直线AB上相遇,而点P旋转到直线AB上的时间分两种情况,所以根据题意列出方程分别求解.
(1)
解:设经过后,点、相遇.
依题意,有,解得,
答:经过后,点、相遇;
(2)
解:点,只能在直线AB上相遇,
则点旋转到直线上的时间为,或.
设点的速度为,则有,解得;
或,解得
答:点的速度为或.
【点睛】此题考查的知识点是一元一次方程的应用,关键是熟练掌握速度、路程、时间的关系.
75.(2022·江苏盐城·七年级期末)某校为承办县初中学校内涵建设,需制作一块活动展板,请来师徒两名工人.已知师傅单独完成需4天,徒弟单独完成需6天.
(1)两个人合作需要多少天完成?
(2)现由徒弟先做1天,师徒两人再合作完成这项工作,问:徒弟共做了几天?
【答案】(1)两个人合作需要天完成
(2)3天
【分析】( 1)设两个人合作需要x天完成,根据师傅完成的工作量+徒弟完成的工作量=总工作量,即可得出关于x的一元一次方程,解之即可求出两个人合作完成这项工作所需时间;
(2 )设徒弟共做了y天,则师傅做了(y﹣1)天,根据师傅完成的工作量+徒弟完成的工作量=总工作量,即可得出关于y的一元一次方程,解之即可求出徒弟共做的时间.
【详解】(1)解:设两个人合作需要x天完成,
依题意得:1,
解得:x.
答:两个人合作需要天完成.
(2)设徒弟共做了y天,则师傅做了(y﹣1)天,
依题意得:1,
解得:y=3.
答:徒弟共做了3天.
【点睛】本题考查列一元一次方程解应用题,掌握列一元一次方程解应用题的方法与步骤是解题关键.
76.(2022·江苏盐城·七年级期末)已知A=3x2+2x﹣1,B=﹣2x2﹣3x+5.求:
(1)A﹣2B;
(2)若2A与3B互为相反数,求x的值.
【答案】(1)7x2+8x﹣11
(2)
【分析】(1)根据整式的加减运算法则计算即可.
(2)根据相反数的性质列出一元一次方程并求解即可.
(1)
解:∵A=3x2+2x﹣1,B=﹣2x2﹣3x+5,
∴A﹣2B
=(3x2+2x﹣1)﹣2(﹣2x2﹣3x+5)
=3x2+2x﹣1+4x2+6x﹣10
=7x2+8x﹣11.
(2)
解:∵2A与3B互为相反数,
∴2A+3B=0.
∵A=3x2+2x﹣1,B=﹣2x2﹣3x+5,
∴2(3x2+2x﹣1)+3(﹣2x2﹣3x+5)=0.
解得.
【点睛】本题考查整式的加减运算,相反数的性质,解一元一次方程,熟练掌握这些知识点是解题关键.
77.(2022·江苏扬州·七年级期末)解方程:
(1);
(2).
【答案】(1)
(2)
【解析】(1)
解:移项,得5x-3x=3+2,
合并同类项,得2x=5
系数化为1,得x=;
(2)
解:去分母,得5(x-3)-2(4x+1)=10,
去括号,得5x-15-8x-2=10,
移项,得5x-8x=10+15+2,
合并同类项,得-3x=27,
系数化为1,得x=-9.
【点睛】本题考查解一元一次方程,熟练掌握解一元一次方程的一般步骤 “去分母,去括号,移项,合并 同类项,系数化为1”是解题的关键.
78.(2022·江苏南京·七年级期末)如图是由一些大小相同的小正方体组合成的简单几何体.
(1)画出该几何体的主视图和左视图;
(2)如果在这个几何体上再添加一些相同的小正方体,并保持俯视图和左视图不变,那么最多可以再添加 块小正方体.
【答案】(1)见解析
(2)5
【分析】(1)根据三视图的定义画出图形即可.
(2)根据题目条件解决问题即可.
(1)
主视图和左视图如下图所示:
(2)
在这个几何体上再添加一些相同的小正方体,并保持俯视图和左视图不变,那么最多可以再添加5块小正方体.
故答案为:5.
【点睛】本题考查作图-三视图,解题的关键是熟练掌握基本知识.
79.(2022·江苏扬州·七年级期末)一个零件的主视图、左视图、俯视图如图所示(尺寸单位:厘米).
(1)写出这个几何体的名称: ;
(2)根据图中数据计算这个几何体的体积和表面积.
【答案】(1)长方体
(2)这个几何体的体积是1800立方厘米,表面积是900平方厘米
【分析】(1)根据三视图即可得出答案;
(2)根据长方体的体积和表面积公式即可得出答案.
(1)
由该几何体的三视图可知该几何体为长方体.
故答案为:长方体;
(2)
根据长方体的体积和表面积公式可知:
V=10×12×15=1800(立方厘米),
S=(10×12+10×15+12×15)×2
=(120+150+180)×2
=450×2
=900(平方厘米).
∴这个几何体的体积是1800立方厘米,表面积是900平方厘米.
【点睛】本题主要考查三视图和长方体的体积和表面积公式,关键是要牢记长方体的体积和表面积公式.
80.(2022·江苏泰州·七年级期末)图①是一个的简单几何体.请在图②的4×4方格纸中分别画出它的主视图、左视图和俯视图(请将所画线加粗).
【答案】见解析
【分析】根据三视图的定义画出图形即可.
【详解】
【点睛】本题考查了几何体的三视图,掌握作三视图的方法是解题的关键.
81.(2022·江苏南京·七年级期末)如图,一个边长为10 cm的无盖正方体可以展开成下面的平面图形.
(1)这个表面展开图的面积是 cm2;
(2)你还能在下面小方格中画出无盖正方体的其他不同形状的表面展开图吗?请画出所有可能的情形(把需要的小正方形涂上阴影);
(3)将一个无盖正方体展开成平面图形的过程中,需要剪开 条棱.
A.3 B.4 C.5 D.不确定
【答案】(1)500
(2)见解析
(3)B
【分析】(1)根据正方形的面积求解即可;
(2)根据正方体的展开图画出表面展开图即可;
(3)根据题意可得,将一个无盖正方体展开成平面图形的过程中,需要剪开4条棱
【详解】(1)
故答案为:
(2)如图所示,
(3)根据题意可得,将一个无盖正方体展开成平面图形的过程中,需要剪开4条棱
故答案为:B
【点睛】本题考查了正方体展开图,掌握正方体的展开图是解题的关键.注意题干是无盖的正方体,所以展开图只有5个面.
82.(2022·江苏南京·七年级期末)在平整的地面上,由若干个完全相同的棱长为的小正方体堆成一个几何体,如图所示.
(1)请你在方格纸中分别画出这个几何体的主视图和左视图;
(2)若现在手头还有一些相同的小正方体,如果保持这个几何体的主视图和俯视图不变,
Ⅰ.在图中所示几何体上最多可以添加______个小正方体;
Ⅱ.在图中所示几何体上最多可以拿走______个小正方体;
【答案】(1)见解析
(2)Ⅰ.添加2个小正方体;Ⅱ.拿走2个小正方体
【分析】对于(1),画出从正面,左面看该组合体看到的图形即可;
对于(2),Ⅰ从俯视图的相应位置增加小正方体,直至主视图不变;
Ⅱ在俯视图的基础上减少小正方体,至主视图不变.
(1)
解:该组合体主视图,左视图如图所示.
(2)
解:Ⅰ在俯视图的相应位置最多相应数量的正方体,如图.
故答案为:2.
Ⅱ在俯视图的相应位置最多减少相应数量的正方体,如图.
故答案为:2.
【点睛】本题主要考查了几何体的三视图,掌握简答组合体的三视图的画法是解题的关键.
83.(2022·江苏无锡·七年级期末)如图由若干个相同的小立方体搭成的一个几何体的主视图和俯视图,俯视图的方格中的字母和数字表示该位置上小立方体的个数.
(1)填空:x= ,y= ;
(2)利用上题结论,先化简再求值:2(3x2y﹣xy2)﹣(xy2+4x2y)+2xy2.
【答案】(1)2,3
(2)2x2y-xy2,6.
【分析】(1)俯视图中的每个数字是该位置小立方体的个数,结合主视图2列中的个数,分析其中的数字,从而求解;
(2)先去括号,再合并同类项化简后代入计算即可求解.
(1)
解:由俯视图可知,该组合体有两行两列,
左边一列前一行有1个正方体,结合主视图可知左边一列叠有2个正方体,故x=2;
由主视图右边一列可知,右边一列最高可以叠3个正方体,故y=3.
故答案为:2,3;
(2)
解:2(3x2y-xy2)-(xy2+4x2y)+2xy2
=6x2y-2xy2-xy2-4x2y+2xy2
=2x2y-xy2,
当x=2,y=3时,
原式=2×22×3-2×32
=2×4×3-2×9
=24-18
=6.
【点睛】本题考查了根据三视图判断几何体的构成以及整式加减中的化简求值.注意找到该几何体的主视图中每列小正方体最多的个数.
84.(2022·江苏·射阳县第六中学七年级期末)如图,是由若干个完全相同的小正方体组成的一个几何体.
(1)请在网格中画出几何体的主视图、左视图、俯视图;
(2)图中共有 个小正方体.
(3)已知每个小正方体的棱长为1cm,则该几何体的表面积为 cm2.
【答案】(1)见解析
(2)6
(3)26
【分析】(1)根据三视图的画法画出相应的图形即可;
(2)观察几何体可得结果;
(3)根据三视图的面积求出该几何体的表面积.
(1)
解:如图所示:
(2)
由图可知:图中共有6个小正方体;
(3)
(4+4+5)×2=26(cm2)
答:该几何体的表面积为26cm2.
【点睛】本题考查解答几何体的三视图,画三视图时应注意“长对正,宽相等,高平齐”.
85.(2022·江苏徐州·七年级期末)如图是用6个棱长为1cm的正方体搭成的几何体.
(1)在所给方格纸中,用实线画出它的三个视图;
(2)该几何体的表面积(含底部)为 cm2.
【答案】(1)见解析
(2)26
【分析】(1)根据三视图的定义,按长对正,高平齐,宽相等的原则在相应位置画出主视图,左视图和俯视图即可;
(2)利用表面积是主视图,左视图与俯视图和的2倍关系求解即可.
(1)
解:主视图是从前面向后看,三列,左边列3个小正方形,中间列1个小正方形,右边列1个小正方形,画出图形得出主视图,左视图从左边向右看2列,左边列3个小正方形,右边列1个性正方形,即可画出主视图,俯视图从上向下看两行,底行中间1个小正方形,上边行3个小正方形,可画出俯视图
(2)
简单组合体的表面积为:2×5+2×4+2×4=10+8+8=26cm2.
故答案为26.
【点睛】本题考查画简单组合体的三视图,与表面积,掌握三视图的画法,表面积求法是解题关键.
86.(2022·江苏淮安·七年级期末)如图是小明用10块棱长都为1cm的正方体搭成的几何体.
(1)分别画出从正面、从左面、从上面看到的所搭几何体的形状图并涂阴影;
(2)小明所搭几何体的表面积(包括与桌面接触的部分)是 .
【答案】(1)见解析
(2)38cm2
【分析】(1)根据几何体的特征可直接进行求解;
(2)由(1)可知前后共有12个小正方形面,左右有12个小正方形面,上下也有12个小正方形面,然后把这些小正方形的面积加起来即为几何体的表面积.
(1)
三视图如图所示:
(2)
由(1)可知:前后共有12个小正方形面,左右有12个小正方形面,上下也有12个小正方形面,还有中间凹槽两个面,
∴小明所搭几何体的表面积(包括与桌面接触的部分)为(12+12+12+2)×1×1=38cm²;
故答案为38cm².
【点睛】本题主要考查从不同角度看几何体,熟练掌握几何体的特征是解题的关键.
87.(2022·江苏江苏·七年级期末)如图,是由几个大小完全相同的小正方体垒成的几何体.
(1)图中共有 个小正方体;
(2)请分别画出你所看到的几何体的三视图(请用黑水笔描清楚).
【答案】(1)6
(2)见解析
【分析】(1)根据几何体的特征解决问题即可;
(2)根据三视图的定义作出图形即可.
(1)
解:图中一共有6个小正方体.
故答案为:6.
(2)
三视图如图所示:
【点睛】本题考查作图﹣三视图,解题的关键是理解三视图的定义,属于中考常考题型.
88.(2022·江苏南京·七年级期末)如图,∠AOB=100°,OC、OD是两条射线,射线OD平分∠BOC,∠BOD=20°.
(1)图中共有 个角;
(2)求∠AOC的度数;
(3)作射线OE.若∠BOE=50°,则∠DOE的度数为 °.
【答案】(1)6
(2)60°
(3)30或70
【分析】(1)数出角的个数即可;
(2)利用角平分线的性质求出∠BOC的度数,即可求出∠AOC;
(3)分类讨论,分为OE在∠AOB的内部或外部,即可求出∠DOE.
(1)
解:一个小角组成的角:3个;两个小角组成的角:2个;三个小角组成的角:1个,共:3+2+1=6个;
故答案为:6;
(2)
解:∵OD 平分∠BOC,∠BOD=20°,
∴∠BOC=2∠BOD=40°.
∵∠AOB=100°,
∴∠AOC=∠AOB-∠BOC=60°;
(3)
解:当OE在∠AOB的内部时,如图1:
∵∠BOE=50°,∠BOD=20°
∴∠DOE=∠BOE-∠BOD=50°-20°=30°;
当OE在∠AOB的内部时,如图2:
∵∠BOE=50°,∠BOD=20°
∴∠DOE=∠BOE+∠BOD=50°+20°=70°
故答案为:30或70.
【点睛】本题考查了角平分线的定义,角的和差运算,灵活应用知识是本题的关键.
89.(2022·江苏扬州·七年级期末)补全下面的解题过程:
如图,已知OC是∠AOB内部的一条射线,OD是∠AOB的平分线,∠AOC=2∠BOC,且∠BOC=40°,求∠COD的度数.
解:∵∠AOC=2∠BOC,∠BOC=40°,
∴∠AOC= °.
∴∠AOB=∠AOC+∠ = °.
∵OD平分∠AOB,
∴∠AOD=∠AOB= °.
∴∠COD=∠ ﹣∠AOD=20°.
【答案】80,BOC,120,60,AOC
【分析】根据题目的已知条件先求出∠AOC,进而求出∠AOB,再根据OD平分∠AOB,求出∠AOD.
【详解】解:∵∠AOC=2∠BOC,∠BOC=40°,
∴∠AOC=80°.
∴∠AOB=∠AOC+∠BOC=120°.
∵OD平分∠AOB,
∴.
∴∠COD=∠AOC﹣∠AOD=20°.
故答案为:80,BOC,120,60,AOC.
【点睛】本题考查了有关角平分线的计算,根据题目已知条件并结合图形去分析是解题的关键.
90.(2022·江苏南京·七年级期末)读句画图.
(1)画射线,连接并延长线段至;
(2)用直尺和圆规作,使得.
【答案】(1)见解析
(2)见解析
【分析】(1)根据射线和线段的定义即可作射线,线段;
(2)利用基本作图(作一个角等于已知角)作,使得.
(1)
如图1,射线,线段即为所求,
(2)
如图2,即为所求,
【点睛】本题考查了作图—基本作图,作射线,线段,作一个角等于已知角,熟练掌握基本作图的方法是解本题的关键.
91.(2022·江苏淮安·七年级期末)如图,C为线段AD上一点,B为CD的中点,AD=20cm,AC=12cm.
(1)图中共有 条线段;
(2)求BD的长;
(3)若点E在线段BD上,且BE=3cm,求AE的长.
【答案】(1)6
(2)BD的长是4cm
(3)AE的长是19cm.
【分析】(1)根据线段的定义找出线段即可;
(2)先根据点B为CD的中点,求出线段CD的长,再根据AC=AD﹣CD即可得出结论;
(3)根据AB=AD﹣BD求出线段AB的长,再根据BE=AB+AE即可得出结论.
(1)
解:图中共有1+2+3=6条线段.
故答案为:6;
(2)
∵AD=20cm,AC=12cm.
∴CD=AD﹣AC=8cm.
∵B为CD的中点.
∵BD=CD=4cm,
(3)
AB=AD﹣BD=20﹣4=16(cm),
AE=AB+BE=16+3=19(cm).
故AE的长是19cm.
【点睛】本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是详解此题的关键.
92.(2022·江苏淮安·七年级期末)如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=25°,求∠COD的度数.
【答案】∠COD的度数是65°
【分析】利用对顶角相等可得∠AOM的度数,再利用角平分线的定义和垂线定义进行计算即可.
【详解】解:∵∠BON=25°,
∴∠AOM=25°,
∵OA平分∠MOD,
∴∠AOD=∠MOA=25°,
∵OC⊥AB,
∴∠AOC=90°,
∴∠COD=90°﹣25°=65°.
答:∠COD的度数是65°.
【点睛】此题主要考查了垂线,关键是掌握对顶角相等,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
93.(2022·江苏淮安·七年级期末)在如图所示的方格纸中,每个小正方形的顶点称为格点,每个小正方形的边长为1,已知四边形ABCD的四个顶点在格点上,利用格点和直尺按下列要求画图:
(1)过点C画AD的平行线CE;
(2)过点B画CD的垂线,垂足为F.
(3)线段CF表示点 到线段 的距离.
【答案】(1)见解析
(2)见解析
(3)C,BF;
【分析】(1)根据平行线的判定画出图形即可;
(2)根据垂线的定义画出图形即可;
(3)根据点到直线的距离的定义,画出图形即可.
(1)
解:如图,直线CE即为所求;
(2)
解:如图,直线BF即为所求;
(3)
解:线段CF的长表示点C到线段BF的距离.
故答案为:C,BF;
【点睛】本题考查画平行线,垂线,点到直线的距离,掌握平行线的性质,点到直线的距离的定义是解题的关键.
94.(2022·江苏泰州·七年级期末)如图,已知,,点D为线段AC的中点,分别求线段CD、BC的长度.
【答案】,.
【分析】根据线段中点的性质推出,再结合图形根据线段之间的和差关系进行求解即可.
【详解】解:∵,点D为线段AC的中点,
∴,
∴.
【点睛】本题考查了线段的中点的意义,线段和差的计算,数形结合是解题的关键.
95.(2022·江苏盐城·七年级期末)如图,点O在直线AB上,CO⊥AB,∠2﹣∠1=34°,OE是∠AOD的平分线,OF⊥OE.
(1)求∠AOE的度数.
(2)找出图中与∠BOF互补的角,并求出∠BOF补角的度数.
【答案】(1)59°
(2)∠AOF;21°
【分析】(1)根据垂线的定义确定∠COB=∠AOC=90°,进而得到∠1+∠2=90°,再根据∠2﹣∠1=34°用∠1表示∠2,进而可求出∠1的度数,根据角的和差关系求出∠AOD的度数,最后根据角平分线的定义即可求出∠AOE.
(2 )根据补角的定义即可得出图中与∠BOF互补的角.根据垂线的定义确定∠EOF=90°,再根据角的和差关系即可求出∠BOF补角的度数.
(1)
解:∵CO⊥AB,
∴∠COB=∠AOC=90°.
∴∠1+∠2=90°.
∵∠2﹣∠1=34°,
∴∠2=∠1+34°.
∴∠1+∠1+34°=90°.
∴∠1=28°.
∴∠AOD=∠AOC+∠1=90°+28°=118°.
∵OE是∠AOD的平分线,
∴.
(2)
解:点O在直线AB上,
∴∠AOF+∠BOF=180°.
∴图中与∠BOF互补的角是∠AOF.
∵OF⊥OE,
∴∠EOF=90°.
∴∠AOF=∠EOF﹣∠AOE=21°.
【点睛】本题考查垂线的定义,角的和差关系,角平分线的定义,补角的定义,熟练掌握这些知识点是解题关键.
96.(2022·江苏宿迁·七年级期末)如图,已知∠AOB=30°,完成下列问题:
(1)在射线OB上取一点C,使OC=2cm;
(2)过点C画直线m,使m//OA;
(3)过点O画直线l,使l⊥OA;
(4)设直线m与直线l交于点D,度量线段OD= cm,∠OCD= 度.
【答案】(1)见解析;
(2)见解析;
(3)见解析;
(4)1;30
【分析】(1)(2)(3)根据要求作出图形即可;
(4)直接利用测量法解决问题即可.
(1)
如下图,线段OC即为所求:
(2)
如上图,直线m即为所求;
(3)
如上图,直线l,点D即为所求;
(4)
通过测量可知,OD=1cm,∠OCD=30°,
故答案为:1,30.
【点睛】本题考查作图﹣复杂作图,平行线的性质,垂线的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
97.(2022·江苏宿迁·七年级期末)如图,,,,求的度数.
【答案】
【分析】根据垂线的定义得到,求出的度数,再求的度数即可.
【详解】解:∵,,
∴,
∵,
∴,
∴.
【点睛】本题考查几何图形中角度的计算,解题的关键是熟练掌握角之间的关系,利用角之间的关系进行计算.
98.(2022·江苏宿迁·七年级期末)在图中“〇”内添上字母A、B、C,使AC<AB<BC.
【答案】见解析
【分析】利用圆规画出弧线,即可得到三角形的三边的大小关系.
【详解】解:如图所示,AC<AB<BC.
【点睛】本题主要考查了比较线段的长短,比较两条线段长短的方法有两种:度量比较法、重合比较法.
99.(2022·江苏盐城·七年级期末)如图,平面上有三个点A、B、C.
(1)根据下列语句按要求画图.
①画射线AB,用圆规在线段AB的延长线上截取BD=AB(保留作图痕迹),连接CA、CD、CB;
②过点C画CE⊥AD,垂足为点E;
③过点D画DF//AC,交CB的延长线于点F.
(2)①在线段CA、CE、CD中,线段______最短,依据是______.
②用刻度尺或圆规检验线段DF与AC的关系为______.
【答案】(1)①见解析;②见解析;③见解析
(2)①CE;直线外一点与直线上各点连接的所有线段中,垂线段最短;②DF=AC,DF//AC
【分析】(1)根据题意作图即可;
(2)根据垂线段最短以及用直尺和圆规进行检验即可.
【详解】(1)①如图所示;
②如图所示;
③如图所示.
(2)①在线段CA、CE、CD中,线段CE最短,依据是直线外一点与直线上各点连接的所有线段中,垂线段最短.
②用刻度尺或圆规检验DF与AC的关系为DF=AC,DF//AC.
【点睛】本题主要考查了画平行线,画垂线,画线段,垂线段最短等等,熟知相关知识是解题的关键.
100.(2022·江苏盐城·七年级期末)已知:如图,A、B、C三点在同一条直线上,BC=3AB,D为AC中点,E为BC中点.若线段AC的长为8,求线段DE的长.
【答案】DE=1.
【分析】根据中点定义求出AD的长度,根据BC=3AB和AC=8,求出AB、BC的长度,由中点定义求出BE的长度,由线段的和差即可求解.
【详解】解:∵D为AC中点,AC=8,
∴AD=AC=4,
∵BC=3AB,AC=8,
∴AB=2,BC=6,
∴,
∵E为BC中点,
∴BE=BC=3,
∴.
【点睛】本题考查两点间的距离,灵活运用中点定义、线段的和差倍数关系是解题的关键.
浙江七年级上学期期末【夯实基础100题专练】-七年级数学上学期考试满分全攻略(浙教版): 这是一份浙江七年级上学期期末【夯实基础100题专练】-七年级数学上学期考试满分全攻略(浙教版),文件包含浙江七年级上学期期末夯实基础100题专练解析版docx、浙江七年级上学期期末夯实基础100题专练原卷版docx等2份试卷配套教学资源,其中试卷共73页, 欢迎下载使用。
2022-2023学年八年级数学上学期期末考试满分全攻略(苏科版)【夯实基础100题考点专练】: 这是一份2022-2023学年八年级数学上学期期末考试满分全攻略(苏科版)【夯实基础100题考点专练】,文件包含江苏八年级上学期期末夯实基础100题考点专练解析版docx、江苏八年级上学期期末夯实基础100题考点专练原卷版docx等2份试卷配套教学资源,其中试卷共52页, 欢迎下载使用。
2022-2023学年九年级数学上学期期末考点大串讲【夯实基础100题考点专练】: 这是一份2022-2023学年九年级数学上学期期末考点大串讲【夯实基础100题考点专练】,共63页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












