高中数学人教A版 (2019)选择性必修 第一册2.3 直线的交点坐标与距离公式教案设计

这是一份高中数学人教A版 (2019)选择性必修 第一册2.3 直线的交点坐标与距离公式教案设计，共6页。教案主要包含了教学内容，教学目标，教学重难点，教学过程等内容，欢迎下载使用。

【教学内容】
两条直线的交点坐标的求法；两条直线的位置关系（相交、平行、重合）的判定方法．
【教学目标】
1．理解并掌握用直线方程求两条相交直线的交点坐标的方法；
2．理解二元一次方程组的解与两条直线的位置的对应关系，会用直线方程组的解和斜率两种方法判断两条直线的位置关系；
3． 提高数形结合能力，初步感悟坐标法的运用，培养提高逻辑推理，数学运算和直观想象素养。
【教学重难点】
教学重点：求两直线的交点坐标的方法、判断两条直线的位置关系的方法.
教学难点：判断两条直线的位置关系的方法.
【教学过程】（说明：本环节包括新授、小结、布置作业等）
（一）引言
在初中平面几何中，我们对直线作定性研究。通过前一阶段的学习，我们把几何图形放入平面直角坐标系中。用坐标来表示点，用二元一次方程来表示直线，实现几何图形的代数化。
这样我们可以通过把握直线上的点，进而用代数方法对直线进行定量研究，例如两条直线的交点坐标。
（二）求解两条直线交点坐标
问题1：已知两条直线，相交，如何求得两条直线的交点坐标？
因为两条直线相交，所以两条直线存在唯一交点，记为.也就是说，点既在直线上也在直线上.因此，同时满足两条直线方程。即，是方程组的唯一解。反之，是方程组的唯一解，说明既在上也在直线上. 所以, 是两条直线的唯一交点. 因此求两条直线的交点，只需联立方程组求解即可.
联立方程组，解得
即，就是两条直线的交点坐标.
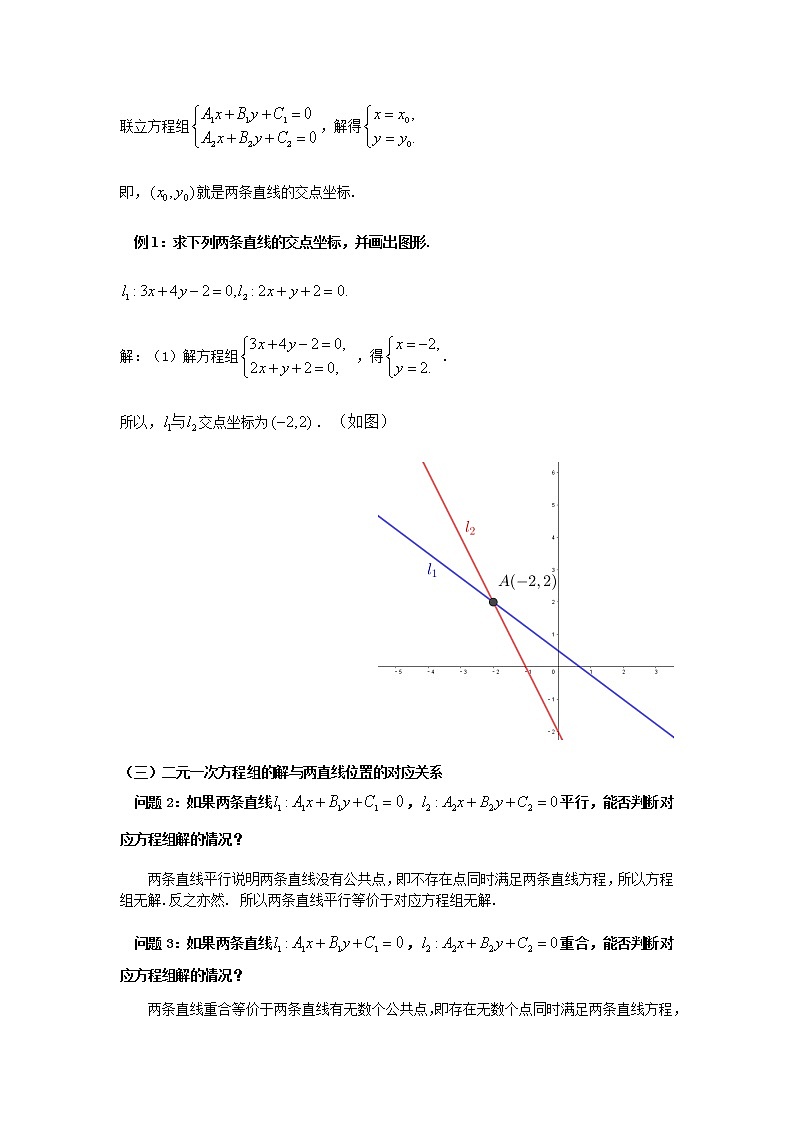
例1：求下列两条直线的交点坐标，并画出图形.
解：（1）解方程组，得.
所以，交点坐标为. （如图）
（三）二元一次方程组的解与两直线位置的对应关系
问题2：如果两条直线，平行，能否判断对应方程组解的情况？
两条直线平行说明两条直线没有公共点，即不存在点同时满足两条直线方程，所以方程组无解.反之亦然. 所以两条直线平行等价于对应方程组无解.
问题3：如果两条直线，重合，能否判断对应方程组解的情况？
两条直线重合等价于两条直线有无数个公共点，即存在无数个点同时满足两条直线方程，所以方程组有无数组解.
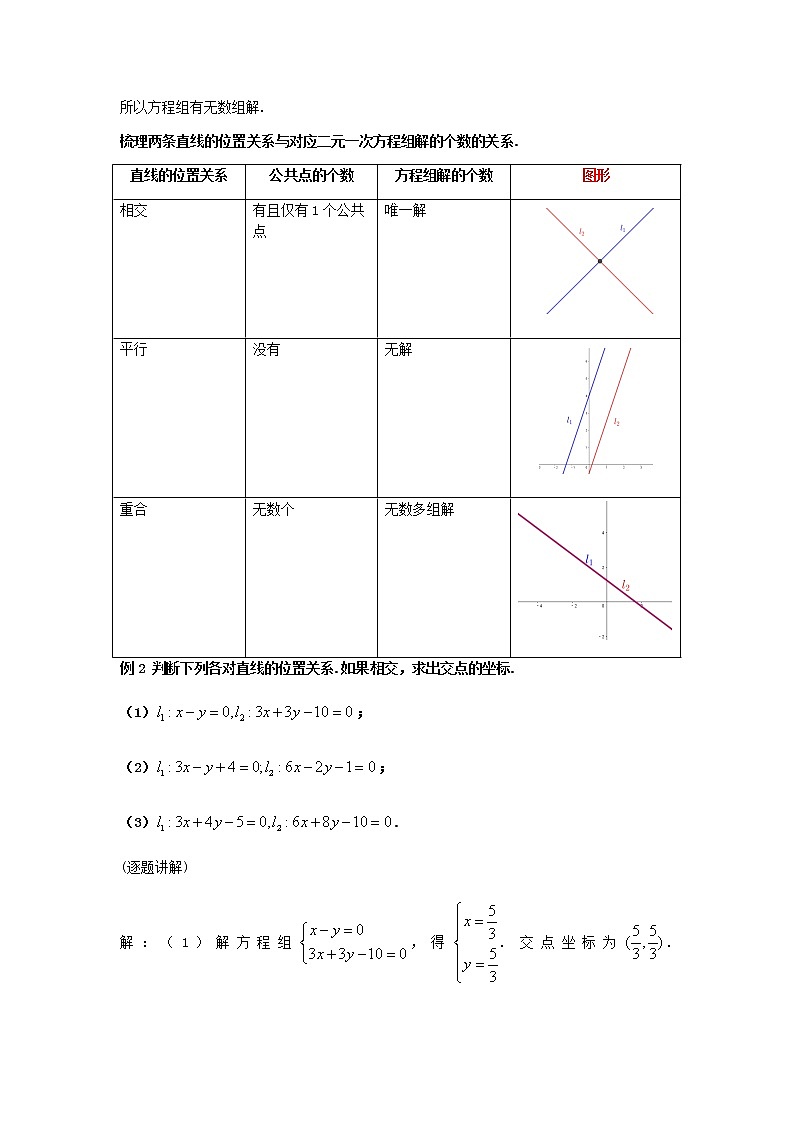
梳理两条直线的位置关系与对应二元一次方程组解的个数的关系.
例2 判断下列各对直线的位置关系.如果相交，求出交点的坐标.
（1）；
（2）；
（3）.
(逐题讲解)
解：（1）解方程组，得. 交点坐标为.
（2）解方程组，方程组无解，
所以，l1与l2无公共点， l1∥l2.
（3）解方程组：，两方程为同一方程，即方程组有无数解，所以两条直线重合.
追问1：题目改为只问“判断下列各对直线的位置关系”，你还有没有其他的判断方法？
用斜率，对于斜率分别为的两条直线，有
.
追问2：能否用直线斜率判断上述两对直线的位置关系？
可以，但关注方程形式，我们所给的直线方程都是一般式.
追问3：如何从直线方程的一般式中确定斜率？
将两条直线方程化为斜截式,找的系数即为斜率.
（1）将两条直线方程化为斜截式，直线，直线与直线的斜率不等，相交.
（2）将两条直线方程化为斜截式，直线，直线与直线的斜率相等，截距不等，平行.
（3）将两条直线方程化为斜截式，直线，直线与直线的斜率与截距均相等，因此两条直线重合.
小结：用斜率判断两直线位置关系
如果两直线斜率都不存在，就看截距：截距相同，则重合；不同则平行
如果两直线一个的斜率不存在，另一个的斜率存在：则相交
如果两直线斜率都存在，就先看斜率：斜率相同，则看截距，若截距不等则平行，若截距相等则重合
问题4：比较用斜率判断和解方程组判断两直线位置关系，你有什么体会？
用斜率能快速判断两条直线平行或相交。解方程组不但可以判断位置关系还可以求交点坐标。但计算量有时较大。当然，如果仅仅判断两直线位置关系， 可以用斜率判断.
归纳总结
回顾本节课的探究过程，说一说你学到了什么？
相交直线交点坐标的求法——通过解方程组求两直线交点坐标；
方程组解的个数与交点个数的关系及判断两直线位置关系的方法.
直线的位置关系
公共点的个数
方程组解的个数
图形
相交
有且仅有1个公共点
唯一解

平行
没有
无解
重合
无数个
无数多组解