





所属成套资源:全套人教版数学八年级下册课堂练素养课件
人教版数学八年级下册集训课堂练素养判定平行四边形的五种常用方法课件
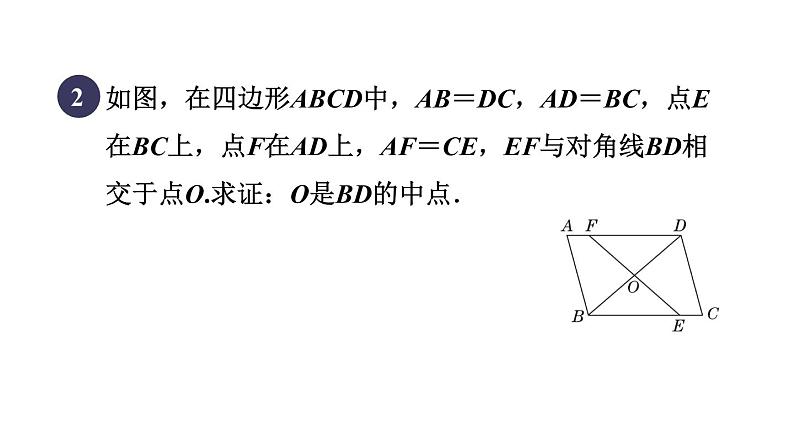
展开
这是一份人教版数学八年级下册集训课堂练素养判定平行四边形的五种常用方法课件,共20页。
人教版 八年级下第十八章 平行四边形判定平行四边形的五种常用方法练素养 课题 集训课堂习题链接如图,在▱ABCD中,E,F分别为AD,BC上的点,且BF=DE,连接AF,CE,BE,DF,AF与BE相交于M点,DF与CE相交于N点.求证:四边形FMEN为平行四边形.1证明:∵四边形ABCD是平行四边形,DE=BF,∴DE BF.∴四边形BFDE为平行四边形.∴BE∥DF.同理,AF∥CE.∴四边形FMEN为平行四边形.2如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O.求证:O是BD的中点.证明:如图,连接BF,DE.∵AB=CD,AD=BC,∴四边形ABCD是平行四边形.∴AD∥BC.∵AF=CE,AD=BC,∴DF=BE.又∵DF∥BE,∴四边形BEDF是平行四边形.∴OB=OD,即O是BD的中点.3如图,已知△ABD,△BCE,△ACF都是等边三角形.求证:四边形ADEF是平行四边形.证明:∵△ABD,△BCE,△ACF都是等边三角形,∴BA=BD=AD,BC=BE,AF=AC,∠DBA=∠EBC=60°.∴∠EBC-∠EBA=∠DBA-∠EBA,即∠ABC=∠DBE.∴△ABC≌△DBE(SAS).∴AC=DE.∴AF=DE.同理可证△ABC≌△FEC,∴AB=FE.∴AD=EF.∴四边形ADEF是平行四边形.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∵点E,F分别是边AB、CD的中点,∴AE=BE=CF=DF,∴四边形AECF是平行四边形,∴AF=CE.4【2022•宿迁】如图,在▱ABCD中,点E,F分别是边AB,CD的中点,求证:AF=CE.56【教材P50习题T10变式】如图,在▱ABCD中,BE平分∠ABC,交AD于点E,DF平分∠ADC,交BC于点F,那么四边形BFDE是平行四边形吗?请说明理由.7【教材P47例4变式】如图,在▱ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.(1)求证:四边形AFCE是平行四边形;证明:∵四边形ABCD是平行四边形,∴DC∥AB,∠DCB=∠DAB=60°.∴∠ADE=∠DAB=∠DCB=∠CBF=60°.∵AE=AD,CF=CB,∴△AED,△CFB是等边三角形.∴∠AEC=∠BFC=60°,∠EAD=∠FCB=60°.∴∠EAF=∠FCE=120°.∴四边形AFCE是平行四边形.解:上述的结论还成立.证明如下:∵四边形ABCD是平行四边形,∴DC=AB,AD=BC,DC∥AB,AD∥BC.∴∠ADE=∠BCD,∠BCD=∠CBF.∴∠ADE=∠CBF.(2)若去掉已知条件的“∠DAB=60°”,上述的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.∵AE=AD,CB=CF,∴∠ADE=∠AED,∠CBF=∠CFB.∴∠AED=∠CFB.又∵∠ADE=∠CBF,AD=CB,∴△ADE≌△CBF(AAS).∴ED=BF,AE=CF.∵DC=AB,∴DC+ED=AB+BF,即EC=AF.又∵AE=CF,∴四边形AECF是平行四边形.8如图①,▱ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.(1)求证:四边形EGFH是平行四边形;(2)如图②,若EF∥AB,GH∥BC,在不添加任何辅助线的情况下,请直接写出图②中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).解:与四边形AGHD面积相等的平行四边形有▱GBCH,▱ABFE,▱EFCD,▱EGFH.






