三角形 （试题）2023年中考数学专题复习 人教版

这是一份三角形 （试题）2023年中考数学专题复习 人教版，共18页。试卷主要包含了下列图形中有稳定性的是，下列哪个图形具有稳定性等内容，欢迎下载使用。
2023年中考数学专题复习--三角形
一．选择题（共10小题）
1．如图，已知BG是∠ABC的平分线，DE⊥AB于点E，DF⊥BC于点F，DE＝5，则DF的长度是（　　）

A．3 B．4 C．5 D．6
2．下列图形中有稳定性的是（　　）
A．平行四边形 B．三角形 C．长方形 D．正方形
3．如图，在△ABC中，CD为边AB的中线，若AB＝12，则AD＝（　　）

A．2 B．3 C．4 D．6
4．在等腰三角形中，有一个角是50°，它的一条腰上的高与底边的夹角是（　　）
A．25° B．25°或40° C．40°或30° D．50°
5．已知等腰三角形的两边长分别为5和11，则它的周长等于（　　）
A．21 B．21或27 C．55 D．27
6．如图，已知AD＝AE，BE＝CD，∠1＝∠2＝100°，∠BAC＝80°，则∠CAE的度数是（　　）

A．20° B．30° C．40° D．50°
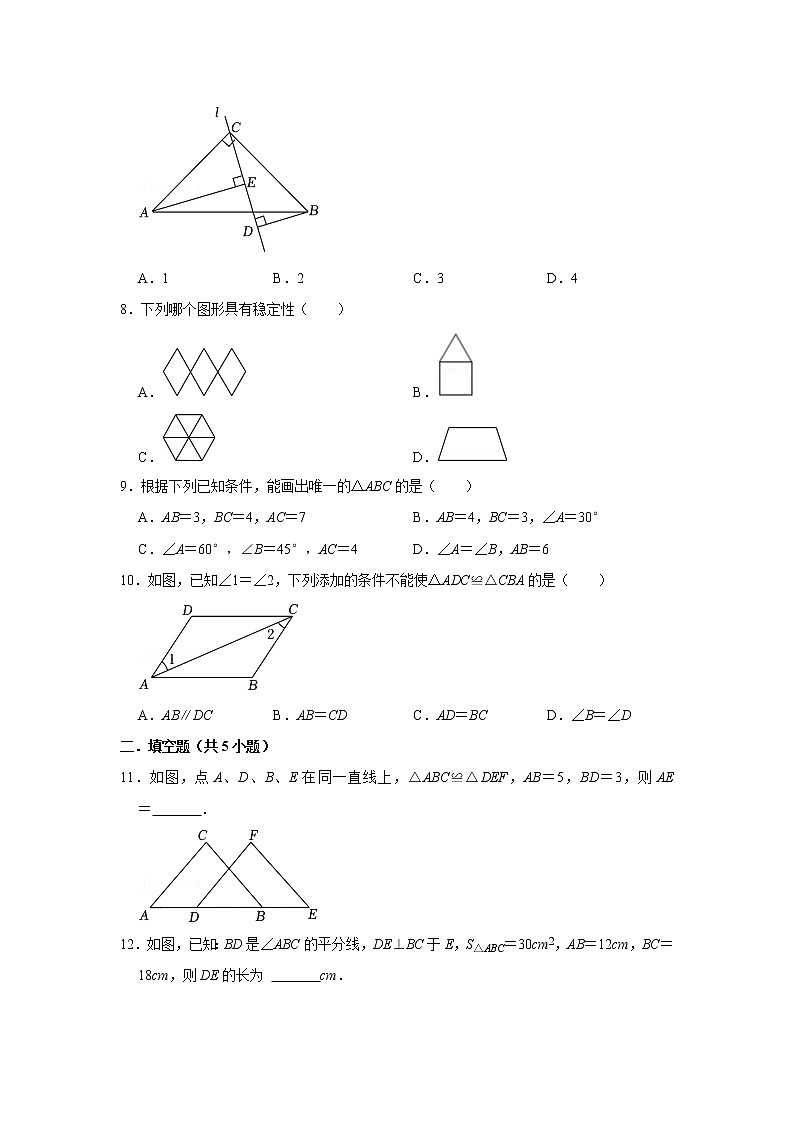
7．如图，在△ABC中，∠ACB＝90°，AC＝BC，直线l过点C且与AB相交，AE⊥l，垂足为点E，BD⊥l，垂足为点D．若AE＝5，BD＝3，则ED的长是（　　）

A．1 B．2 C．3 D．4
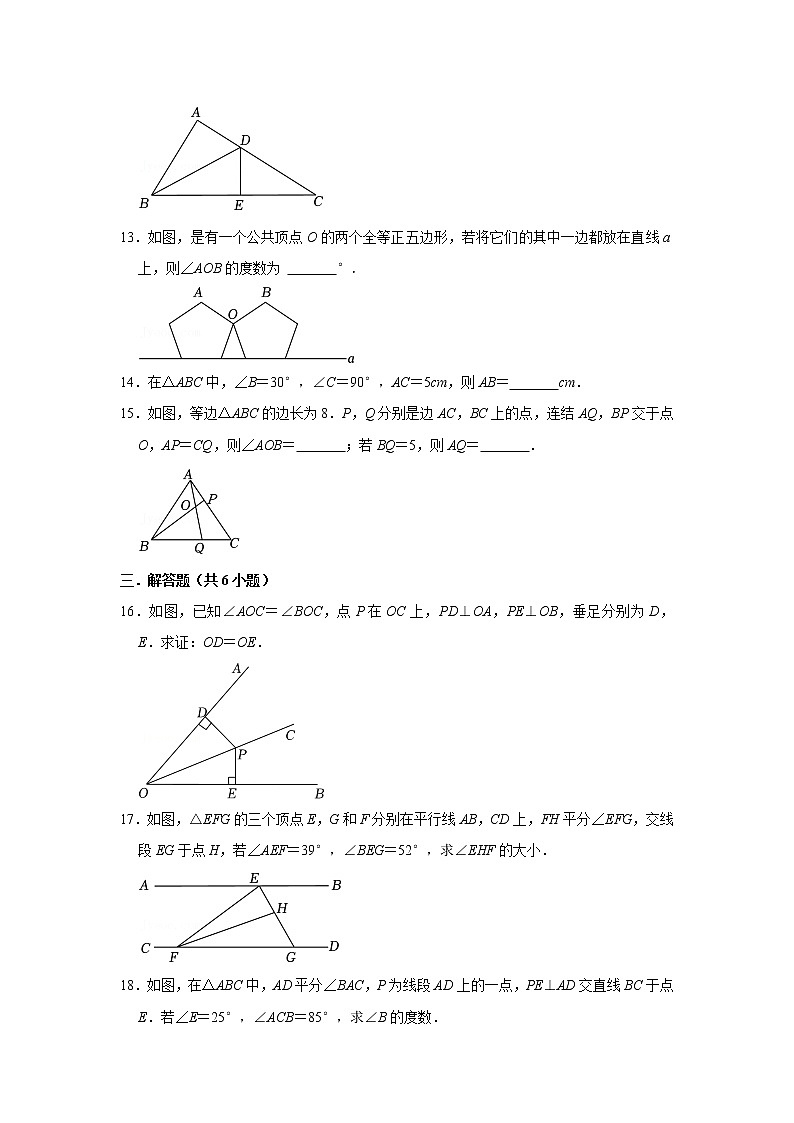
8．下列哪个图形具有稳定性（　　）
A． B．
C． D．
9．根据下列已知条件，能画出唯一的△ABC的是（　　）
A．AB＝3，BC＝4，AC＝7 B．AB＝4，BC＝3，∠A＝30°
C．∠A＝60°，∠B＝45°，AC＝4 D．∠A＝∠B，AB＝6
10．如图，已知∠1＝∠2，下列添加的条件不能使△ADC≌△CBA的是（　　）

A．AB∥DC B．AB＝CD C．AD＝BC D．∠B＝∠D
二．填空题（共5小题）
11．如图，点A、D、B、E在同一直线上，△ABC≌△DEF，AB＝5，BD＝3，则AE＝　 　．

12．如图，已知：BD是∠ABC的平分线，DE⊥BC于E，S△ABC＝30cm2，AB＝12cm，BC＝18cm，则DE的长为 　 　cm．

13．如图，是有一个公共顶点O的两个全等正五边形，若将它们的其中一边都放在直线a上，则∠AOB的度数为 　 　°．

14．在△ABC中，∠B＝30°，∠C＝90°，AC＝5cm，则AB＝　 　cm．
15．如图，等边△ABC的边长为8．P，Q分别是边AC，BC上的点，连结AQ，BP交于点O，AP＝CQ，则∠AOB＝　 　；若BQ＝5，则AQ＝　 　．

三．解答题（共6小题）
16．如图，已知∠AOC＝∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D，E．求证：OD＝OE．

17．如图，△EFG的三个顶点E，G和F分别在平行线AB，CD上，FH平分∠EFG，交线段EG于点H，若∠AEF＝39°，∠BEG＝52°，求∠EHF的大小．

18．如图，在△ABC中，AD平分∠BAC，P为线段AD上的一点，PE⊥AD交直线BC于点E．若∠E＝25°，∠ACB＝85°，求∠B的度数．

19．如图，在四边形ABCD中，AC⊥BC，AB＝13，BC＝12，CD＝3，AD＝4．
（1）求AC的长；
（2）求四边形ABCD的面积．

20．如图，AB＝AC，AC的垂直平分线交AB于D，交AC于E．
（1）若∠A＝50°，求∠BCD的度数；
（2）若AE＝7，△BCD的周长为23，求△ABC的周长．

21．已知：AO＝DO，EO＝FO，BE＝CF，AB＝CD．请证明：△AOB≌△DOC．


2023年中考数学专题复习--三角形
参考答案与试题解析
一．选择题（共10小题）
1．如图，已知BG是∠ABC的平分线，DE⊥AB于点E，DF⊥BC于点F，DE＝5，则DF的长度是（　　）

A．3 B．4 C．5 D．6
【分析】根据角平分线的性质定理解答即可．
【解答】解：∵BG是∠ABC的平分线，DE⊥AB，DF⊥BC，
∴DF＝DE＝5，
故选：C．
【点评】本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．
2．下列图形中有稳定性的是（　　）
A．平行四边形 B．三角形 C．长方形 D．正方形
【分析】根据三角形具有稳定性，四边形不具有稳定性即可得出答案．
【解答】解：三角形具有稳定性，四边形不具有稳定性，
故选：B．
【点评】本题考查了三角形的稳定性，掌握三角形具有稳定性是解题的关键．
3．如图，在△ABC中，CD为边AB的中线，若AB＝12，则AD＝（　　）

A．2 B．3 C．4 D．6
【分析】根据三角形中线的概念解答即可．
【解答】解：∵CD为边AB的中线，
∴D为AB的中点，
∴AD＝AB＝6．
故选：D．
【点评】本题考查了三角形中线的概念，三角形一边的中点与此边所对顶点的连线叫做三角形的中线．
4．在等腰三角形中，有一个角是50°，它的一条腰上的高与底边的夹角是（　　）
A．25° B．25°或40° C．40°或30° D．50°
【分析】根据题意先画出图形，再分两种情况：50°为底角和50°为顶角求出答案．
【解答】解：当50°为顶角时，

∵∠A＝50°，
∠B＝∠ACB＝65°，
∴∠BCD＝25°；
当50°为底角时，

∵∠B＝∠ACB＝50°，
∴∠BCD＝40°．
故选：B．
【点评】本题考查了等腰三角形的性质以及三角形的内角和定理，是基础知识要熟练掌握．注意分类讨论思想的应用．
5．已知等腰三角形的两边长分别为5和11，则它的周长等于（　　）
A．21 B．21或27 C．55 D．27
【分析】分两种情况：当等腰三角形的腰长为5，底边长为11时，当等腰三角形的腰长为11，底边长为5时，然后分别进行计算即可解答．
【解答】解：分两种情况：
当等腰三角形的腰长为5，底边长为11时，
∵5+5＝10＜11，
∴不能组成三角形，
当等腰三角形的腰长为11，底边长为5时，
则它的周长＝11+11+5＝27，
综上所述：则它的周长等于27，
故选：D．
【点评】本题考查了等腰三角形的性质，三角形的三边关系，分两种情况进行计算是解题的关键．
6．如图，已知AD＝AE，BE＝CD，∠1＝∠2＝100°，∠BAC＝80°，则∠CAE的度数是（　　）

A．20° B．30° C．40° D．50°
【分析】先利用平角定义求出∠ADE＝80°，∠AED＝80°，从而利用三角形内角和定理求出∠DAE＝20°，进而可得∠BAD+∠CAE＝60°，然后利用等式的性质可得BD＝CE，从而利用SAS证明△ADB≌△AEC，最后利用全等三角形的性质可得∠BAD＝∠CAE＝30°，即可解答．
【解答】解：∵∠1＝∠2＝100°，
∴∠ADE＝180°﹣∠1＝80°，∠AED＝180°﹣∠2＝80°，
∴∠DAE＝180°﹣∠ADE﹣∠AED＝20°，
∵∠BAC＝80°，
∴∠BAD+∠CAE＝∠BAC﹣∠DAE＝60°，
∵BE＝CD，
∴BE﹣DE＝CD﹣DE，
∴BD＝CE，
在△ADB和△AEC中，
，
∴△ADB≌△AEC（SAS），
∴∠BAD＝∠CAE＝30°，
故选：B．
【点评】本题考查了全等三角形的判定与性质，等腰三角形的性质，熟练掌握全等三角形的判定与性质是解题的关键．
7．如图，在△ABC中，∠ACB＝90°，AC＝BC，直线l过点C且与AB相交，AE⊥l，垂足为点E，BD⊥l，垂足为点D．若AE＝5，BD＝3，则ED的长是（　　）

A．1 B．2 C．3 D．4
【分析】根据垂直的定义及直角三角形的性质推出∠AEC＝∠CDB＝90°，∠BCD＝∠CAE，利用AAS证明△ACE≌△CBD，根据全等三角形的性质及线段的和差求解即可．
【解答】解：∵∠ACB＝90°，AE⊥l，BD⊥l，
∴∠ACE+∠BCD＝90°，∠AEC＝∠CDB＝90°，
∴∠ACE+∠CAE＝90°，
∴∠BCD＝∠CAE，
在△ACE和△CBD中，
，
∴△ACE≌△CBD（AAS），
∴AE＝CD＝5，CE＝BD＝3，
∴DE＝CD﹣CE＝2，
故选：B．
【点评】此题考查了全等三角形的判定与性质，利用AAS证明△ACE≌△CBD是解题的关键．
8．下列哪个图形具有稳定性（　　）
A． B．
C． D．
【分析】根据三角形具有稳定性判断即可．
【解答】解：A、图形不具有稳定性，本选项不符合题意；
B、图形不具有稳定性，本选项不符合题意；
C、图形具有稳定性，本选项符合题意；
D、图形不具有稳定性，本选项不符合题意；
故选：C．
【点评】本题考查的是三角形的性质，熟记三角形具有稳定性是解题的关键．
9．根据下列已知条件，能画出唯一的△ABC的是（　　）
A．AB＝3，BC＝4，AC＝7 B．AB＝4，BC＝3，∠A＝30°
C．∠A＝60°，∠B＝45°，AC＝4 D．∠A＝∠B，AB＝6
【分析】根据全等三角形的判定定理和三角形的三边关系理逐个判断即可．
【解答】解：A、3+4＜7，不符合三角形的三边关系定理，不能画出三角形，故本选项不符合题意；
B、AB＝4，BC＝3，∠A＝30°，不符合全等三角形的判定定理，不能画出唯一的三角形，故本选项不符合题意；
C、∠A＝60°，∠B＝45°，AC＝4，符合全等三角形的判定定理AAS，能画出唯一的三角形，故本选项符合题意；
D、∠A＝∠B，AB＝6，不符合全等三角形的判定定理，不能画出唯一的三角形，故本选项不符合题意；
故选：C．
【点评】本题考查了全等三角形的判定定理和三角形三边关系定理，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，两直角三角形全等还有HL．
10．如图，已知∠1＝∠2，下列添加的条件不能使△ADC≌△CBA的是（　　）

A．AB∥DC B．AB＝CD C．AD＝BC D．∠B＝∠D
【分析】由全等三角形的判定依次判断可求解．
【解答】解：A、由AB∥CD，可得∠DCA＝∠CAB，且∠1＝∠2，AC＝AC，能判定△ADC≌△CBA（ASA），故选项A不符合题意；
B、由AB＝CD，且∠1＝∠2，AC＝AC，不能判定△ADC≌△CBA，故选项B符合题意；
C、由AD＝BC，且∠1＝∠2，AC＝AC，能判定△ADC≌△CBA（SAS），故选项C不符合题意；
D，由∠B＝∠D，且∠1＝∠2，AC＝AC，能判定△ADC≌△CBA（AAS），故选项D不符合题意；
故选：B．
【点评】本题考查了全等三角形的判定，熟练运用全等三角形的判定方法是本题的关键．
二．填空题（共5小题）
11．如图，点A、D、B、E在同一直线上，△ABC≌△DEF，AB＝5，BD＝3，则AE＝　7　．

【分析】求出AD的长，再根据全等三角形对应边相等可得DE＝AB，然后根据AE＝AD+DE代入数据计算即可得解．
【解答】解：∵AB＝5，BD＝3，
∴AD＝AB﹣BD＝5﹣3＝2，
∵△ABC≌△DEF，
∴DE＝AB＝5，
∴AE＝AD+DE＝2+5＝7．
故答案为：7．
【点评】本题考查了全等三角形的性质，熟记性质并准确识图，理清图中线段之间的关系是解题的关键．
12．如图，已知：BD是∠ABC的平分线，DE⊥BC于E，S△ABC＝30cm2，AB＝12cm，BC＝18cm，则DE的长为 　2　cm．

【分析】过点D作DF⊥AB于F，根据角平分线上的点到角的两边距离相等可得DE＝DF，再根据S△ABC＝S△ABD+S△BCD列出方程求解即可．
【解答】解：如图，过点D作DF⊥AB于F，
∵BD是∠ABC的平分线，DE⊥BC，
∴DE＝DF，
S△ABC＝S△ABD+S△BCD，
＝AB•DF+BC•DE，
＝×12•DE+×18•DE，
＝15DE，
∵S△ABC＝30cm2，
∴15DE＝30，
解得DE＝2cm．
故答案为：2．

【点评】本题考查了角平分线上的点到角的两边距离相等的性质，三角形的面积，熟记性质并作辅助线是解题的关键．
13．如图，是有一个公共顶点O的两个全等正五边形，若将它们的其中一边都放在直线a上，则∠AOB的度数为 　108　°．

【分析】根据正五边形的性质和图形全等的性质得到∠1＝∠2＝∠3＝∠4＝108°，再利用邻补角的定义计算出∠OCD＝∠ODC＝72°，接着根据三角形内角和定理计算出∠COD＝36°，然后利用周角的定义计算出∠AOB的度数．
【解答】解：如图，
∵两图形为全等的正五边形，
∴∠1＝∠2＝∠3＝∠4＝108°，
∴∠OCD＝∠ODC＝180°﹣108°＝72°，
∴∠COD＝180°﹣72°﹣72°＝36°，
∴∠AOB＝360°﹣∠1﹣∠3﹣∠COD＝360°﹣108°﹣108°﹣36°＝108°．
故答案为：108．

【点评】本题考查了全等图形：掌握全等图形的定义和正五边形的性质是解决问题的关键．
14．在△ABC中，∠B＝30°，∠C＝90°，AC＝5cm，则AB＝　10　cm．
【分析】利用含30度角的直角三角形的性质，即可解决问题．
【解答】解：∵∠ACB＝90°，∠B＝30°，AC＝5cm，
∴AB＝2AC＝10cm，
故答案为：10．
【点评】本题考查含30度角的直角三角形的性质，解题的关键是熟练掌握基本知识，属于中考常考题型．
15．如图，等边△ABC的边长为8．P，Q分别是边AC，BC上的点，连结AQ，BP交于点O，AP＝CQ，则∠AOB＝　120°　；若BQ＝5，则AQ＝　7　．

【分析】由“SAS”可证△ABP≌△ACQ，由全等三角形的性质可得∠ABP＝∠CAQ，由外角的性质可求出∠AOB＝120°，过点A作AD⊥BC于D，求出AD和DQ的长，由勾股定理可得出答案．
【解答】解：∵△ABC是等边三角形，
∴AB＝AC，∠BAC＝∠C＝60°，
在△ABP与△ACQ中，
，
∴△ABP≌△ACQ（SAS），
∴∠ABP＝∠CAQ，
∴∠BOQ＝∠ABO+∠BAQ＝∠CAQ+∠BAQ＝∠BAC＝60°，
∴∠AOB＝120°；
过点A作AD⊥BC于D，

∵BC＝8，△ABC是等边三角形，
∴BD＝CD＝4，∠ABD＝60°，
∴AD＝＝＝4，
∵BQ＝5，
∴DQ＝1，
∴AQ＝＝＝7，
故答案为：120°，7．
【点评】本题考查了全等三角形的判定和性质，等边三角形的性质，直角三角形的性质，证明三角形全等是解题的关键．
三．解答题（共6小题）
16．如图，已知∠AOC＝∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D，E．求证：OD＝OE．

【分析】证明△POD≌△POE，根据全等三角形的性质证明结论．
【解答】证明：∵PD⊥OA，PE⊥OB，
∴∠PDO＝∠PEO＝90°，
在△POD和△POE中，
，
∴△POD≌△POE（AAS），
∴OD＝OE．
【点评】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理是解题的关键．
17．如图，△EFG的三个顶点E，G和F分别在平行线AB，CD上，FH平分∠EFG，交线段EG于点H，若∠AEF＝39°，∠BEG＝52°，求∠EHF的大小．

【分析】利用∠AEF＝39°，∠BEG＝52°，可以求出∠FEG＝89°，再利用FH平分∠EFG，可以求出∠EFH的度数，最后利用三角形的内角和即可求解．
【解答】解：∵∠AEF＝39°，∠BEG＝52°，
∴∠FEG＝180°﹣∠AEF﹣∠BEG＝89°，
∵AB∥CD，
∴∠EFG＝∠AEF＝39°，
∵FH平分∠EFG，
∴∠EFH＝，
在△EFH中，
则∠EHF＝180°﹣∠EFH﹣∠FEG＝180°﹣19.5°﹣89°＝71.5°．
答：∠EHF的度数为71.5°．
【点评】本题主要考查三角形的内角和定理和角平分线的定义，解题的关键是熟练掌握三角形的内角和是180°
18．如图，在△ABC中，AD平分∠BAC，P为线段AD上的一点，PE⊥AD交直线BC于点E．若∠E＝25°，∠ACB＝85°，求∠B的度数．

【分析】先根据直角三角形的性质求出∠ADE的度数，再根据三角形的内角和定理求得∠DAC的度数，再根据角平分线的定义求得∠BAC的度数，从而根据三角形的内角和定理即可得解．
【解答】解：∵PE⊥AD，
∴∠E+∠ADE＝90°，
∵∠E＝25°，
∴∠ADE＝90°﹣∠E＝65°，
∵∠ACB＝85°，
∴∠DAC＝180°﹣∠ADE﹣∠ACB＝30°，
∵AD平分∠BAC，
∴∠BAC＝2∠DAC＝60°，
∴∠B＝180°﹣∠ACB﹣∠BAC＝35°．
【点评】此题主要考查了三角形内角和定理，角平分线的定义，解答的关键是结合图形分析清楚角与角之间的关系．
19．如图，在四边形ABCD中，AC⊥BC，AB＝13，BC＝12，CD＝3，AD＝4．
（1）求AC的长；
（2）求四边形ABCD的面积．

【分析】（1）根据垂直定义可得∠ACB＝90°，然后在Rt△ABC中，利用勾股定理进行计算即可解答；
（2）先利用勾股定理的逆定理证明△ADC是直角三角形，从而可得∠D＝90°，然后根据四边形ABCD的面积＝△ADC的面积+△ABC的面积，进行计算即可解答．
【解答】解：（1）∵AC⊥BC，
∴∠ACB＝90°，
∵AB＝17，BC＝8，
∴AC＝＝＝5，
∴AC的长为5；
（2）∵AD2+CD2＝42+32＝25，AC2＝52＝25，
∴AD2+CD2＝AC2，
∴△ADC是直角三角形，
∴∠D＝90°，
∴四边形ABCD的面积＝△ADC的面积+△ABC的面积
＝AD•CD+AC•BC
＝×4×3+12×5
＝6+30
＝36，
∴四边形ABCD的面积为36．
【点评】本题考查了勾股定理，勾股定理的逆定理，熟练掌握勾股定理，以及勾股定理的逆定理是解题的关键．
20．如图，AB＝AC，AC的垂直平分线交AB于D，交AC于E．
（1）若∠A＝50°，求∠BCD的度数；
（2）若AE＝7，△BCD的周长为23，求△ABC的周长．

【分析】（1）先利用等腰三角形的性质，以及三角形内角和定理可得∠B＝∠ACB＝65°，再利用线段垂直平分线的性质可得AD＝CD，从而可得∠ACD＝∠A＝50°，然后利用角的和差关系进行计算即可解答；
（2）利用线段垂直平分线的性质可得AD＝DC，AC＝2AE＝14，再根据已知△BCD的周长为23，可得BC+AB＝23，然后利用三角形的周长公式进行计算即可解答．
【解答】解：（1）∵AB＝AC，∠A＝50°，
∴∠B＝∠ACB＝（180°﹣∠A）＝65°，
∵DE垂直平分线AC，
∴AD＝CD，
∴∠ACD＝∠A＝50°，
∴∠BCD＝∠ACB﹣∠ACD＝65°﹣50°＝15°，
∴∠BCD的度数为15°；
（2）∵DE垂直平分线AC，AE＝7，
∴AD＝DC，AC＝2AE＝14，
∵△BCD的周长为23，
∴BC+CD+DB＝23，
∴BC+AD+BD＝23，
∴BC+AB＝23，
∴△ABC的周长＝AB+BC+AC＝14+23＝37，
∴△ABC的周长为37．
【点评】本题考查了等腰三角形的性质，线段垂直平分线的性质，熟练掌握等腰三角形的性质，以及线段垂直平分线的性质是解题的关键．
21．已知：AO＝DO，EO＝FO，BE＝CF，AB＝CD．请证明：△AOB≌△DOC．

【分析】先证明BO＝CO，然后根据“SAS”可判断：△AOB≌△DOC．
【解答】证明：∵EO＝FO，BE＝CF，
∴EO+BE＝FO+CF，
即BO＝CO，
在△AOB和△DOC中，
，
∴△AOB≌△DOC（SAS）．
【点评】本题考查了全等三角形的判定：熟练掌握全等三角形的5种判定方法是解决问题的关键；选用哪一种方法，取决于题目中的已知条件．