2019-2020学年内蒙古鄂尔多斯市东胜区七年级（上）期末数学试卷

这是一份2019-2020学年内蒙古鄂尔多斯市东胜区七年级（上）期末数学试卷，共19页。

2019-2020学年内蒙古鄂尔多斯市东胜区七年级（上）期末数学试卷
一．单项选择题（本大题10个小题，每小题3分，共30分）
1．（3分）下列四个数中，其相反数是负整数的是（　　）
A． B．|﹣4| C．﹣1 D．
2．（3分）鄂尔多斯市体育中心有“一场两馆”，即体育场，综合体育馆和游泳馆，总建筑面积约25.9万平方米，将25.9万用科学记数法表示为（　　）
A．25.9×104 B．2.59×104 C．25.9×105 D．2.59×105
3．（3分）下列各组数值相等的是（　　）
A．（﹣3）2和﹣32 B．和
C．|﹣32|和﹣（﹣32） D．﹣（﹣2）3和﹣23
4．（3分）把任意有理数对（x，y）放进装有计算x+y2+1装置的魔术盒，例如：把（﹣1，2）放入其中，就会得到﹣1+22+1＝4．如果把（﹣5，﹣7）放入魔盒，则得到的是（　　）
A．43 B．44 C．45 D．46
5．（3分）下列结论错误的是（　　）
A．若mx＝my，则x＝y B．若x＝3，则x2＝3x
C．若，则a＝b D．若2x﹣3＝3x，则﹣x＝3
6．（3分）如图，一艘轮船行驶在O处同时测得小岛A、B的方向分别为北偏东75°和西南方向，则∠AOB等于（　　）

A．100° B．120° C．135° D．150°
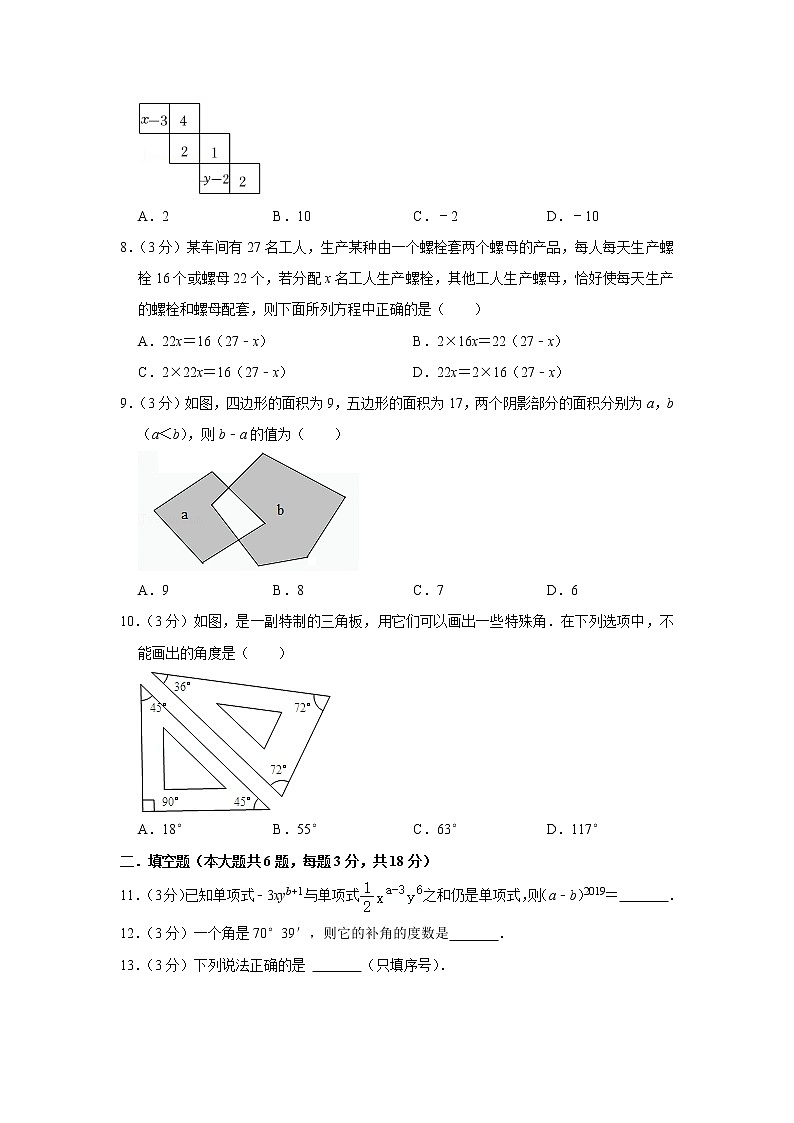
7．（3分）如图，是一个正方体的展开图，如果相对面上的两个式子表示的数相等，则x+y的值为（　　）

A．2 B．10 C．﹣2 D．﹣10
8．（3分）某车间有27名工人，生产某种由一个螺栓套两个螺母的产品，每人每天生产螺栓16个或螺母22个，若分配x名工人生产螺栓，其他工人生产螺母，恰好使每天生产的螺栓和螺母配套，则下面所列方程中正确的是（　　）
A．22x＝16（27﹣x） B．2×16x＝22（27﹣x）
C．2×22x＝16（27﹣x） D．22x＝2×16（27﹣x）
9．（3分）如图，四边形的面积为9，五边形的面积为17，两个阴影部分的面积分别为a，b（a＜b），则b﹣a的值为（　　）

A．9 B．8 C．7 D．6
10．（3分）如图，是一副特制的三角板，用它们可以画出一些特殊角．在下列选项中，不能画出的角度是（　　）

A．18° B．55° C．63° D．117°
二．填空题（本大题共6题，每题3分，共18分）
11．（3分）已知单项式﹣3xyb+1与单项式之和仍是单项式，则（a﹣b）2019＝　 　．
12．（3分）一个角是70°39′，则它的补角的度数是　 　．
13．（3分）下列说法正确的是 　 　（只填序号）．
①单项式的系数为，次数为4；②用两个钉子把一根细木条钉在木板上的数学原理是：两点之间，线段最短；③已知xa+a＝3是关于x的一元一次方程，则该方程的解为x＝2；④等角的补角相等；⑤0既不是单项式也不是多项式．
14．（3分）已知当x＝2时，多项式ax3+bx+1的值是10，求当x＝﹣2时，多项式ax3+bx+1的值是 　 　．
15．（3分）有理数a，b，c在数轴上对应的点的位置如图所示，有下列结论：①a+b＞0；②（b﹣c）（c﹣a）＞0；③|a﹣b|+|a﹣c|＝|b﹣c|；④，其中正确的有 　 　．（只填序号）

16．（3分）下列图形都是由同样大小的菱形按照一定规律所组成的，其中第①个图形中一共有3个菱形，第②个图形中一共有7个菱形，第③个图形中一共有13个菱形，…，按此规律排列下去，第n个图形中菱形的个数为　 　．

三．解答题（本大题共8题，共72分.解答时要写出必要的文字说明，演算步骤或推理过程）
17．（13分）（1）计算：．
（2）解方程：．
（3）先化简，再求值：x﹣（x﹣y2）+2（x+y2），其中（x+2）2+|y﹣1|＝0．
18．（6分）天意长城汽车销售店计划2019年下半年6个月每月销售20辆汽车，由于某种原因未能按计划执行，实际每月的销量情况如下（规定比计划月销量增加为正，减少为负）：+4，﹣2，﹣1，0，+2，+3．
（1）销量最多的一个月比销量最少的一个月多销售 　 　辆．
（2）这半年内实际平均每月销售了多少辆汽车？
19．（6分）已知多项式A，B，其中B＝5x2+3x﹣4，马小虎同学在计算“A+B”时，误将“A+B”看成了“A﹣B”，求得的结果为12x2﹣6x+7．
（1）求多项式A；
（2）当x＝﹣1时，求A+B的值．
20．（8分）甲、乙两工程队想共同承包修筑一条公路．甲队单独做120天完成，乙队单独做80天完成，合同规定50天完成．否则每超出一天罚款800元，甲、乙经过商量后签订合同．
（1）正常情况下，甲、乙两队能否在合同期内完成工程，为什么？
（2）现两队合做完成了这项工程的，因甲队别处有急事被调走，剩下的由乙队完成，结果是否需要缴纳罚款？若缴纳罚款，需交纳多少罚款；若不缴纳，说明理由．
21．（6分）【阅读理解】阅读下列内容，观察分析，回答问题：
Ⅰ.33×34＝（3×3×3）×（3×3×3×3）＝37；
Ⅱ.53×54＝（5×5×5）×（5×5×5×5）＝57；
Ⅲ．a3×a4＝（a×a×a）×（a×a×a×a）＝a7．
【概括总结】通过以上分析，填空am×an＝（）×（）＝（）＝a（②）（m、n为正整数）．
①中填 　 　，
②中填 　 　．
【应用与拓展】计算：
③105×104＝　 　；
④a•a5•a7＝　 　；
⑤如果a10＝8，a2＝5，则a12＝　 　．
22．（10分）某旅行社准备在寒假期间面向学生推出“延安两日游”活动，收费标准如下表：
人数m
0＜m＜100
100≤m≤200
m＞200
收费标准（元/人）
120
95
85
甲、乙两所学校计划组织本校学生自愿参加此项活动，已知甲校报名参加的学生人数小于200人且大于等于100人，乙校报名参加的学生人数少于100人．经核算，若两校联合组团只需花费20400元，若两校分别组团共需花费25050元．
（1）两所学校一共有多少学生报名参加旅游？
（2）两所学校报名参加旅游的学生各有多少人？
（3）在不允许个人售卖的情况下，如果甲校有60名学生因有事不能外出游玩，那么他们该如何购买门票才能最省钱？
23．（11分）如图：在数轴上点A表示数﹣4，点O表示数0，点B表示数6．点P为数轴上任意一点，其对应的数为x．

（1）如果点P到点A，点B的距离相等，那么x的值是 　 　；
（2）数轴上是否存在点P，使点P到A点，点B的距离之和为12？若存在，请求出x的值；若不存在，请说明理由；
（3）若点A，O，B开始在数轴上匀速向右运动，其速度分别为4个单位长度/秒，3个单位长度/秒，1个单位长度/秒，设运动时间为t秒，请直接写出OA＝3OB时的时间．

24．（12分）【初步探究】
（1）如图1，已知线段AB＝12，点C和点D为线段AB上的两个动点，且CD＝3cm，点M，N分别是AC和BD的中点．求MN的长是多少cm？
【类比探究】
（2）如图2，已知，直角∠COD与平角∠AOB如图摆放在一起，且OM和ON分别是∠AOC，∠BOD的角平分线，则∠MON的度数为多少度？
【知识迁移】
（3）当∠AOB＝α，∠COD＝β时，如图3摆放在一起，且OM和ON分别是∠AOC，∠BOD的角平分线，则∠MON的度数为多少度？（α和β均为小于平角的角）



2019-2020学年内蒙古鄂尔多斯市东胜区七年级（上）期末数学试卷
参考答案与试题解析
一．单项选择题（本大题10个小题，每小题3分，共30分）
1．（3分）下列四个数中，其相反数是负整数的是（　　）
A． B．|﹣4| C．﹣1 D．
【解答】解：A、的相反数是﹣，不符合题意；
B、|﹣4|＝4的相反数是﹣4，符合题意；
C、﹣1的相反数是1，不符合题意；
D、﹣的相反数是，不符合题意．
故选：B．
2．（3分）鄂尔多斯市体育中心有“一场两馆”，即体育场，综合体育馆和游泳馆，总建筑面积约25.9万平方米，将25.9万用科学记数法表示为（　　）
A．25.9×104 B．2.59×104 C．25.9×105 D．2.59×105
【解答】解：25.9万＝259000＝2.59×105．
故选：D．
3．（3分）下列各组数值相等的是（　　）
A．（﹣3）2和﹣32 B．和
C．|﹣32|和﹣（﹣32） D．﹣（﹣2）3和﹣23
【解答】解：A选项，9≠﹣9，故该选项不符合题意；
B选项，≠，故该选项不符合题意；
C选项，9＝9，故该选项符合题意；
D选项，8≠﹣8，故该选项不符合题意；
故选：C．
4．（3分）把任意有理数对（x，y）放进装有计算x+y2+1装置的魔术盒，例如：把（﹣1，2）放入其中，就会得到﹣1+22+1＝4．如果把（﹣5，﹣7）放入魔盒，则得到的是（　　）
A．43 B．44 C．45 D．46
【解答】解：由题意得：
﹣5+（﹣7）2+1
＝﹣5+49+1
＝45．
故选：C．
5．（3分）下列结论错误的是（　　）
A．若mx＝my，则x＝y B．若x＝3，则x2＝3x
C．若，则a＝b D．若2x﹣3＝3x，则﹣x＝3
【解答】解：∵m可能为0，
∴利用等式性质2，由mx＝my得到x＝y是错误的，
∴选项A符合题意；
∵由等式的性质2，x＝3的两边都乘以x得到x2＝3x是正确的，
∴选项B不符合题意；
∵当成立时，m﹣1≠0，
∴由等式性质2，两边都乘以m﹣1得a＝b是正确的，
∴选项C不符合题意；
由等式的性质1，2x﹣3＝3x通过移项、合并同类项可得﹣x＝3，
∴选项D不符合题意，
故选：A．
6．（3分）如图，一艘轮船行驶在O处同时测得小岛A、B的方向分别为北偏东75°和西南方向，则∠AOB等于（　　）

A．100° B．120° C．135° D．150°
【解答】解：∵A、B的方向分别为北偏东75°和西南方向
∠AOB＝15°+45°+90°＝150°．
故选：D．
7．（3分）如图，是一个正方体的展开图，如果相对面上的两个式子表示的数相等，则x+y的值为（　　）

A．2 B．10 C．﹣2 D．﹣10
【解答】解：由正方体表面展开图的“相间、Z端是对面”可知，
“x﹣3”与“1”相对，
“﹣y﹣2”与“4”相对，
∵相对的面上的数相等，
∴x＝4，y＝﹣6，
∴x+y＝4﹣6＝﹣2，
故选：C．
8．（3分）某车间有27名工人，生产某种由一个螺栓套两个螺母的产品，每人每天生产螺栓16个或螺母22个，若分配x名工人生产螺栓，其他工人生产螺母，恰好使每天生产的螺栓和螺母配套，则下面所列方程中正确的是（　　）
A．22x＝16（27﹣x） B．2×16x＝22（27﹣x）
C．2×22x＝16（27﹣x） D．22x＝2×16（27﹣x）
【解答】解：∵分配x名工人生产螺栓，
∴分配（27﹣x）名工人生产螺母．
依题意得：2×16x＝22（27﹣x）．
故选：B．
9．（3分）如图，四边形的面积为9，五边形的面积为17，两个阴影部分的面积分别为a，b（a＜b），则b﹣a的值为（　　）

A．9 B．8 C．7 D．6
【解答】解：设重叠部分面积为c，
b﹣a＝（b+c）﹣（a+c）＝17﹣9＝8．
故选：B．
10．（3分）如图，是一副特制的三角板，用它们可以画出一些特殊角．在下列选项中，不能画出的角度是（　　）

A．18° B．55° C．63° D．117°
【解答】解：A、18°＝90°﹣72°，则18°角能画出；
B、55°不能写成36°、72°、45°、90°的和或差的形式，不能画出；
C、63°＝90°﹣72°+45°，则63°可以画出；
D、117°＝72°+45°，则117°角能画出．
故选：B．
二．填空题（本大题共6题，每题3分，共18分）
11．（3分）已知单项式﹣3xyb+1与单项式之和仍是单项式，则（a﹣b）2019＝　﹣1　．
【解答】解：∵单项式﹣3xyb+1与单项式之和仍是单项式，
∴a﹣3＝1，6＝b+1，
∴a＝4，b＝5，
∴（a﹣b）2019＝（4﹣5）2＝（﹣1）2＝﹣1，
故答案为：﹣1．
12．（3分）一个角是70°39′，则它的补角的度数是　109°21′　．
【解答】解：∵该角度数为70°39′，
∴它的补角的度数＝180°﹣70°39′＝109°21′．
故答案为：109°21′．
13．（3分）下列说法正确的是 　③④　（只填序号）．
①单项式的系数为，次数为4；②用两个钉子把一根细木条钉在木板上的数学原理是：两点之间，线段最短；③已知xa+a＝3是关于x的一元一次方程，则该方程的解为x＝2；④等角的补角相等；⑤0既不是单项式也不是多项式．
【解答】解：单项式的系数为﹣，次数为3，因此①不正确；
用两个钉子把一根细木条钉在木板上的数学原理是：两点确定一条直线，因此②不正确；
已知xa+a＝3是关于x的一元一次方程，则a＝1，该方程变为x+1＝3，解得x＝2，即该方程的解为x＝2，因此③正确；
等角的补角相等是正确的，因此④正确；
0是单项式，因此⑤不正确；
综上所述，正确的有③④，
故答案为：③④．
14．（3分）已知当x＝2时，多项式ax3+bx+1的值是10，求当x＝﹣2时，多项式ax3+bx+1的值是 　﹣8　．
【解答】解：∵当x＝2时，多项式ax3+bx+1的值是10，
∴8a+2b+1＝10．
∴8a+2b＝9．
∴当x＝﹣2时，
多项式ax3+bx+1
＝﹣8a﹣2b+1
＝﹣（8a+2b）+1
＝﹣9+1
＝﹣8．
故答案为：﹣8．
15．（3分）有理数a，b，c在数轴上对应的点的位置如图所示，有下列结论：①a+b＞0；②（b﹣c）（c﹣a）＞0；③|a﹣b|+|a﹣c|＝|b﹣c|；④，其中正确的有 　③④　．（只填序号）

【解答】解：由数轴可得b＜0＜a＜c，|a|＜|b|＜|c|，
∴a+b＜0，故①错误；
∵b﹣c＜0，c﹣a＞0，
∴（b﹣c）（c﹣a）＜0，故②错误；
∵a﹣b＞0，a﹣c＜0，b﹣c＜0，
∴|a﹣b|+|a﹣c|＝a﹣b﹣a+c＝c﹣b，
|b﹣c|＝c﹣b，故③正确；
∵b＜0，a＞0，c＞0，
∴＝1﹣1+1＝1，故④正确．
故答案为：③④．
16．（3分）下列图形都是由同样大小的菱形按照一定规律所组成的，其中第①个图形中一共有3个菱形，第②个图形中一共有7个菱形，第③个图形中一共有13个菱形，…，按此规律排列下去，第n个图形中菱形的个数为　n2+n+1　．

【解答】解：第①个图形中一共有3个菱形，3＝12+2；
第②个图形中共有7个菱形，7＝22+3；
第③个图形中共有13个菱形，13＝32+4；
…，
第n个图形中菱形的个数为：n2+n+1；
故答案为：n2+n+1．
三．解答题（本大题共8题，共72分.解答时要写出必要的文字说明，演算步骤或推理过程）
17．（13分）（1）计算：．
（2）解方程：．
（3）先化简，再求值：x﹣（x﹣y2）+2（x+y2），其中（x+2）2+|y﹣1|＝0．
【解答】解：（1）原式＝﹣9+2×2+17
＝﹣9+4+17
＝12；
（2）去分母得，3 （x﹣1）﹣2（x+1）＝﹣6，
去括号得，3x﹣3﹣2x﹣2＝﹣6，
移项、合并同类项得，x＝﹣1；
（3）原式＝x﹣x+y2+2x+2y2＝2x+3y2，
∵（x+2）2+|y﹣1|＝0，
∴x+2＝0，y﹣1＝0，
解得x＝﹣2，y＝1，
∴原式＝2×（﹣2）+3×12＝﹣4+3＝﹣1．
18．（6分）天意长城汽车销售店计划2019年下半年6个月每月销售20辆汽车，由于某种原因未能按计划执行，实际每月的销量情况如下（规定比计划月销量增加为正，减少为负）：+4，﹣2，﹣1，0，+2，+3．
（1）销量最多的一个月比销量最少的一个月多销售 　6　辆．
（2）这半年内实际平均每月销售了多少辆汽车？
【解答】解：（1）4﹣（﹣2）＝6（辆），
故答案为6．
（2）4+（﹣2）+（﹣1）+0+2+（+3）＝6（辆），
∴6个月的总销售量为20×6+6＝126（辆），
平均每月销售量为126÷6＝21（辆），
答：这半年内实际平均每月销售了6辆汽车．
19．（6分）已知多项式A，B，其中B＝5x2+3x﹣4，马小虎同学在计算“A+B”时，误将“A+B”看成了“A﹣B”，求得的结果为12x2﹣6x+7．
（1）求多项式A；
（2）当x＝﹣1时，求A+B的值．
【解答】解：（1）根据题意知，A＝（12x2﹣6x+7）+（5x2+3x﹣4）
＝12x2﹣6x+7+5x2+3x﹣4
＝17x2﹣3x+3；
（2）A+B
＝（17x2﹣3x+3）+（5x2+3x﹣4）
＝17x2﹣3x+3+5x2+3x﹣4
＝22x2﹣1，
当x＝﹣1时，
原式＝22×（﹣1）2﹣1
＝22×1﹣1
＝22﹣1
＝21．
20．（8分）甲、乙两工程队想共同承包修筑一条公路．甲队单独做120天完成，乙队单独做80天完成，合同规定50天完成．否则每超出一天罚款800元，甲、乙经过商量后签订合同．
（1）正常情况下，甲、乙两队能否在合同期内完成工程，为什么？
（2）现两队合做完成了这项工程的，因甲队别处有急事被调走，剩下的由乙队完成，结果是否需要缴纳罚款？若缴纳罚款，需交纳多少罚款；若不缴纳，说明理由．
【解答】解：（1）甲、乙两人能在合同期内完成工程，理由如下：
设甲、乙两人合作x天完成该工程，
依题意得：+＝1，
解得：x＝48，
∵48＜50，
∴甲、乙两人能在合同期内完成工程．
（2）两人合做完成了这项工程的所需时间为÷（+）＝36（天）．
设乙队还需y天完成剩下的工程，
依题意得：＝1﹣，
解得：y＝20．
∵36+20＝56（天），56＞50，
∴结果需要缴纳罚款，
又∵800×（56﹣50）＝4800（元），
∴需交纳4800元罚款．
答：需要缴纳罚款，需交纳4800元罚款．
21．（6分）【阅读理解】阅读下列内容，观察分析，回答问题：
Ⅰ.33×34＝（3×3×3）×（3×3×3×3）＝37；
Ⅱ.53×54＝（5×5×5）×（5×5×5×5）＝57；
Ⅲ．a3×a4＝（a×a×a）×（a×a×a×a）＝a7．
【概括总结】通过以上分析，填空am×an＝（）×（）＝（）＝a（②）（m、n为正整数）．
①中填 　m+n　，
②中填 　m+n　．
【应用与拓展】计算：
③105×104＝　109　；
④a•a5•a7＝　a13　；
⑤如果a10＝8，a2＝5，则a12＝　40　．
【解答】解：①m+n，
②m+n，
③105×104＝105+4＝109，
④a•a5•a7＝a1+5+7＝a13，
⑤a12＝a10•a2＝8×5＝40，
故答案为：①m+n，
②m+n，
③109，
④a13，
⑤40．
22．（10分）某旅行社准备在寒假期间面向学生推出“延安两日游”活动，收费标准如下表：
人数m
0＜m＜100
100≤m≤200
m＞200
收费标准（元/人）
120
95
85
甲、乙两所学校计划组织本校学生自愿参加此项活动，已知甲校报名参加的学生人数小于200人且大于等于100人，乙校报名参加的学生人数少于100人．经核算，若两校联合组团只需花费20400元，若两校分别组团共需花费25050元．
（1）两所学校一共有多少学生报名参加旅游？
（2）两所学校报名参加旅游的学生各有多少人？
（3）在不允许个人售卖的情况下，如果甲校有60名学生因有事不能外出游玩，那么他们该如何购买门票才能最省钱？
【解答】解：（1）设两校人数之和为a，
若a＞200，则a＝20400÷85＝240；
若100≤a≤200，则a＝20400÷95＝214＞200，不合题意，
答：两所学校报名参加旅游的学生人数之和等于240人；
（2）设甲学校报名参加旅游的学生有x人，乙学校报名参加旅游的学生有y人，则：
，解得，
答：甲学校报名参加旅游的学生有150人，乙学校报名参加旅游的学生有90人；
（3）方案一：各自购买门票需（150﹣60）×120+90×120＝21600（元）；
方案二：联合购买门票需（240﹣60）×95＝17100（元）；
方案三：联合购买门票201张需201×85＝17085（元）．
∵21600＞17100＞17085，
∴甲、乙两校联合起来选择按85元/人购买201张门票最省钱．
23．（11分）如图：在数轴上点A表示数﹣4，点O表示数0，点B表示数6．点P为数轴上任意一点，其对应的数为x．

（1）如果点P到点A，点B的距离相等，那么x的值是 　1　；
（2）数轴上是否存在点P，使点P到A点，点B的距离之和为12？若存在，请求出x的值；若不存在，请说明理由；
（3）若点A，O，B开始在数轴上匀速向右运动，其速度分别为4个单位长度/秒，3个单位长度/秒，1个单位长度/秒，设运动时间为t秒，请直接写出OA＝3OB时的时间．

【解答】解：（1）∵点P到点A，点B的距离相等，
∴x﹣（﹣4）＝6﹣x，
解得x＝1，
故答案为：1；
（2）存在，
当x＜﹣4时，（﹣4﹣x）+（6﹣x）＝12，解得x＝﹣5，
当﹣4≤x≤6时，x﹣（﹣4）+（6﹣x）＝12，无解；
当x＞6时，x﹣（﹣4）+x﹣6＝12，解得x＝7，
综上所述，x的值为﹣5或7；
（3）运动后A表示的数为﹣4+4t，O边上的数为3t，B表示得数为6+t，
∴OA＝|﹣4+4t﹣3t|＝|t﹣4|，OB＝|3t﹣6﹣t|＝|2t﹣6|，
∵OA＝3OB，
∴|t﹣4|＝3•|2t﹣6|，
解得t＝或t＝．
24．（12分）【初步探究】
（1）如图1，已知线段AB＝12，点C和点D为线段AB上的两个动点，且CD＝3cm，点M，N分别是AC和BD的中点．求MN的长是多少cm？
【类比探究】
（2）如图2，已知，直角∠COD与平角∠AOB如图摆放在一起，且OM和ON分别是∠AOC，∠BOD的角平分线，则∠MON的度数为多少度？
【知识迁移】
（3）当∠AOB＝α，∠COD＝β时，如图3摆放在一起，且OM和ON分别是∠AOC，∠BOD的角平分线，则∠MON的度数为多少度？（α和β均为小于平角的角）


【解答】解：（1）∵AB＝12，CD＝3，
∴AC+BD＝9，
∵点M，N分别是AC和BD的中点，
∴MC＝AC，DN＝BD，
∴MC+DN＝4.5，
∴MN＝MC+CD+DN＝7.5；
（2）∵∠AOB＝180°，∠COD＝90°，
∴∠AOC+∠BOD＝90°，
∵OM和ON分别是∠AOC，∠BOD的角平分线，
∴∠MOC＝∠AOC，∠DON＝∠DOC，
∴∠MOC+∠DON＝45°，
∴∠MON＝∠MOC+∠COD+∠DON＝135°；
（3）∵OM和ON分别是∠AOC，∠BOD的角平分线，
∴∠MOC＝∠AOC，∠BON＝∠BOD，
∴∠MON＝∠MOC+∠COB+∠BON
＝∠AOC+∠COB+∠BOD
＝（∠AOC+2∠COB+∠BOD）
＝（∠AOB+∠COD）
＝．
:35:19；