



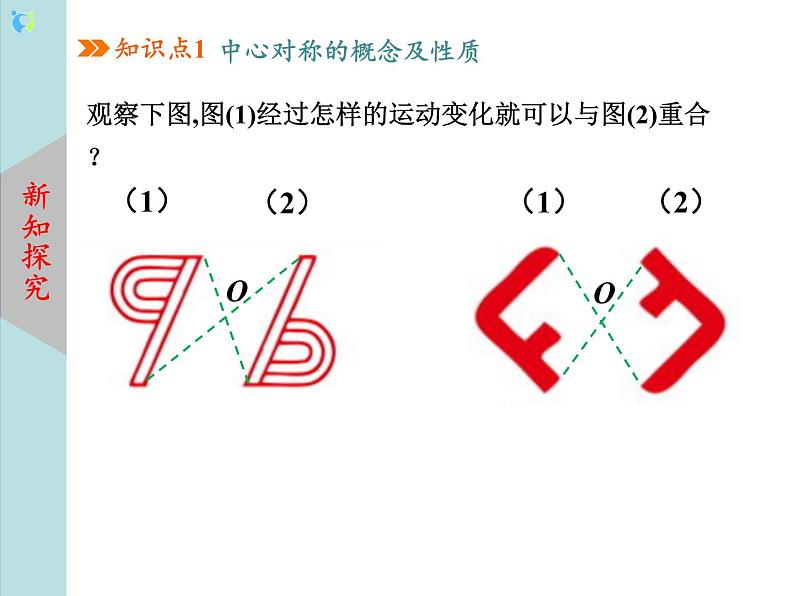


北师大版第三章 图形的平移与旋转3 中心对称优秀课件ppt
展开八年级数学下册北师大版
《3.3中心对称》教学设计
课题名 | 3.3中心对称 |
教学目标 | 1.知识与技能:了解中心对称、中心对称图形的概念;掌握中心对称的性质;掌握能够运用中心对称的性质作图的方法. 2.过程与方法:经历有关中心对称的观察、操作、欣赏和设计过程,进一步积累数学活动经验. 3.情感态度和价值观:通过发展学生综合运用变换解决有关问题的能力, 激发学生的好奇心和求知欲望,获得成功的体验. |
教学重点 | 能判断一个图形是否为中心对称图形;利用中心对称的性质进行作图. |
教学难点 | 中心对称与中心对称图形的联系与区别;运用中心对称的性质作图的方法. |
教学准备 | 教师准备:课件 学生准备:常规用具 |
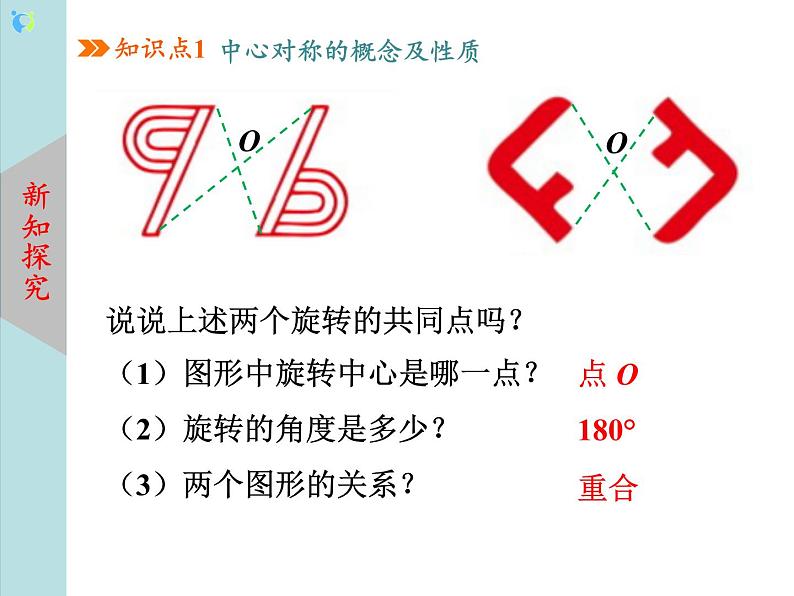
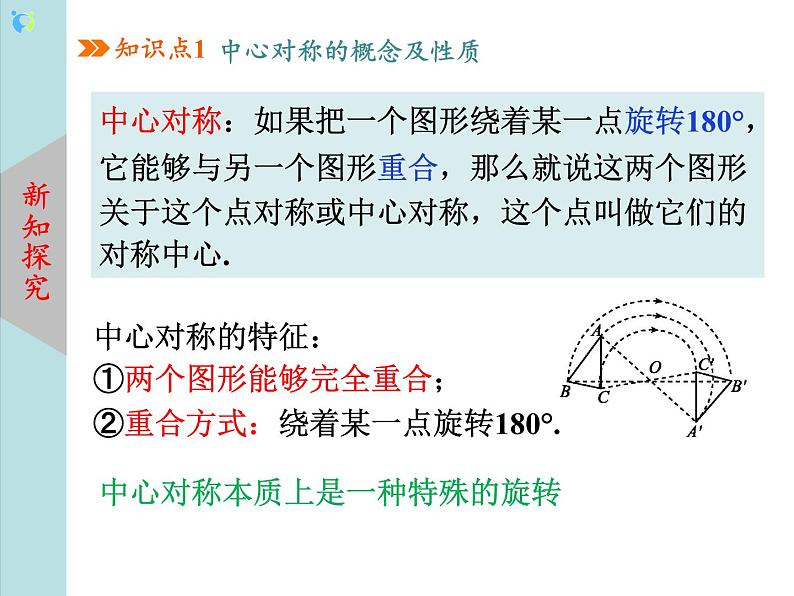
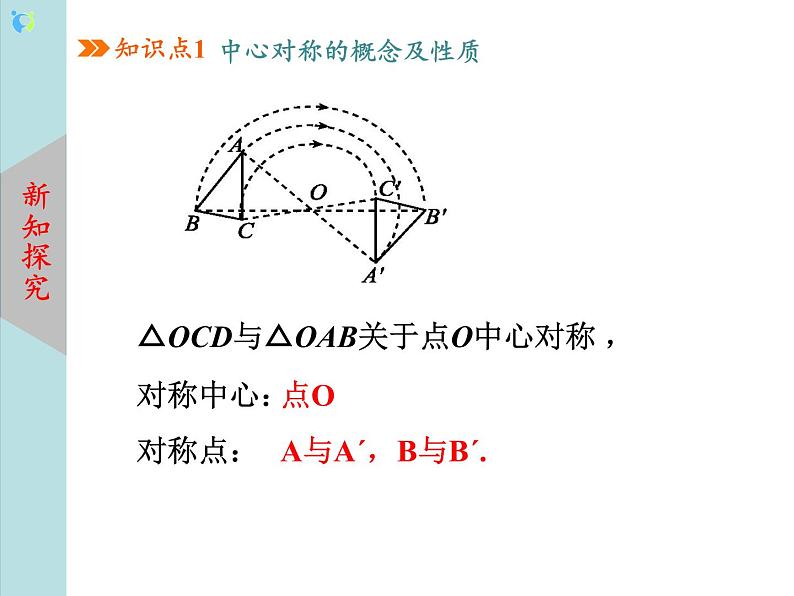
教学过程 | 一、 新课导入 知识回顾:1. (1)观察下面图形,看看它们是否是轴对称图形? (2) 什么是轴对称图形? 2.观察下面的两个图形还是轴对称图形吗?你有什么发现? 设计意图:教师通过多媒体展示(展示画面)回顾旧知,轴对称的具体实例,同时展示成中心对称的图形,进行对比导入新知. 二、 新知讲授 知识点一:中心对称的概念及性质 中心对称:如果把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心. 中心对称的特征: ①两个图形能够完全重合; ②重合方式:绕着某一点旋转180°. 中心对称的性质:成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.(即对称点与对称中心三点共线) 对称中心的确定:方法1:对称中心为任意两个对应点连接的线段的中点; 方法2:对称中心为任意两组对应点连接的线段的交点. 轴对称和中心对称的比较: 设计意图:通过观察类比、习题巩固、表格分析等多种方式让学生对知识一目了然,运用自如,充分发挥学生的主体性和主观能动性. 例1 下列各组图形中,△A'B'C'与△ABC成中心对称的是( ) 例2 如图,点O是线段AE的中点,以点O为对称中心,画出与五边形ABCDE成中心对称的图形. 画已知图形关于某点成中心对称的图形的“四步法” (1)连接(2)延长(3)截取(4)画图 知识点二:中心对称图形 中心对称图形:把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合, 那么这个图形叫做中心对称图形,这个点叫做它的对称中心. 中心对称图形是指一个图形. 设计意图:学生在观察、分析、归纳的基础上,提炼出中心对称和中心对称图形的概念,并在理解概念的基础上,进一步提炼出它们的性质,再用比较的方法对比轴对称,深刻领会了中心对称. 三、知识巩固 1.如图所示的5组图形中,左边的图形与右边的图形成中心对称的有( ) A.1组 B.2组 C.3组 D.4组 2. 下列图形中,可以看作是中心对称图形的是( ) 3. 如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′,ED=BC,线段ED经旋转后变为线段E′D′. 已知BC=4,则线段E′D′的长度为( ) A.2 B.3 C.4 D.1.5 4. 如图,△ABC与△A1B1C1关于点O成中心对称,下列法:①∠BAC=∠B1A1C1;②AC=A1C1;③OA=OA1; ④△ABC与△A1B1C1的面积相等.其中正确的有( ) A.1个 B.2个 C.3个 D.4个 5.如图, 在平面直角坐标系中, 若△ABC与△A1B1C1关于E点成中心对称, 则对称中心E点的坐标是________. 6. 下列常见几何图形中,轴对称图形的有 ,中心对称图形的有 ,既是轴对称图形又是中心对称图形的有 . ①线段 ②角 ③等边三角形 ④平行四边形 ⑤矩形 ⑥菱形 ⑦圆 ⑧ 等腰梯形 7. 下列图形中,既是轴对称图形又是中心对称图形的是( ) 8. 如图,直线EF经过平行四边形ABCD的对角线的交点O,若AE=2 cm,四边形AEFB的面积为12 cm2,则CF= ,平行四边形ABCD的面积为 . 拓展练习:9. 已知△ABC在平面直角坐标系中的位置如图所示. (1)作△ABC关于点C成中心对称的△A1B1C; (2)将△A1B1C向右平移4个单位长度,作出平移后的△A2B2C2; (3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标. 四、课堂小结 中心对称与中心对称图形的区别与联系: |
布置作业 | 教材84页1,2题 |
板书设计 | 3.3中心对称
|
教学反思 | 本节课是建立在“轴对称”、“图形的旋转”基础之上,进一步学习特殊的图形旋转——中心对称,主要介绍中心对称的概念和性质。本节课的重点是中心对称的概念;难点是中心对称的性质和应用。 为了使学生感受、理解知识的产生和发展过程,鉴于本节教学内容的特点和学生的心理特征,我确定了以启发、实践、交流为主的教学方法。努力培养学生观察、思考、交流、合作的学习品质和猜想、类比、归纳、概括的思维习惯,对激发学生探索精神和创新意识等方面都具有重要意义。为了培养学生的抽象思维,我通过了大量课件,把动态的问题直观地表现出来,使学生更容易理解并掌握中心对称的概念和性质。 本节课,从学生已有的生活经验出发,引导学生通过各种形式的活动,从数学的角度去观察事物、思考问题,使学生真正实现由“学会”到“会学”的质的飞跃。通过创设情景,学生观察探究,习题巩固较好掌握本节课的内容,是一节高效课堂. |
数学八年级下册第三章 图形的平移与旋转3 中心对称教学课件ppt: 这是一份数学八年级下册第三章 图形的平移与旋转3 中心对称教学课件ppt,文件包含北师大版数学八年级下册33中心对称同步课件pptx、北师大版数学八年级下册33中心对称教学设计含教学反思docx等2份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
北师大版八年级下册3 中心对称授课ppt课件: 这是一份北师大版八年级下册3 中心对称授课ppt课件,共19页。PPT课件主要包含了引入课题,探究新知,课堂小结,本节课学了哪些知识,布置作业,教材习题36等内容,欢迎下载使用。
初中数学北师大版八年级下册第三章 图形的平移与旋转3 中心对称课文ppt课件: 这是一份初中数学北师大版八年级下册第三章 图形的平移与旋转3 中心对称课文ppt课件,共34页。PPT课件主要包含了情境引入,魔术时间,情境引入2,旋转角为180°,观察与思考,中心对称的概念及性质,知识要点,归纳总结,找一找,中心对称的性质等内容,欢迎下载使用。














