
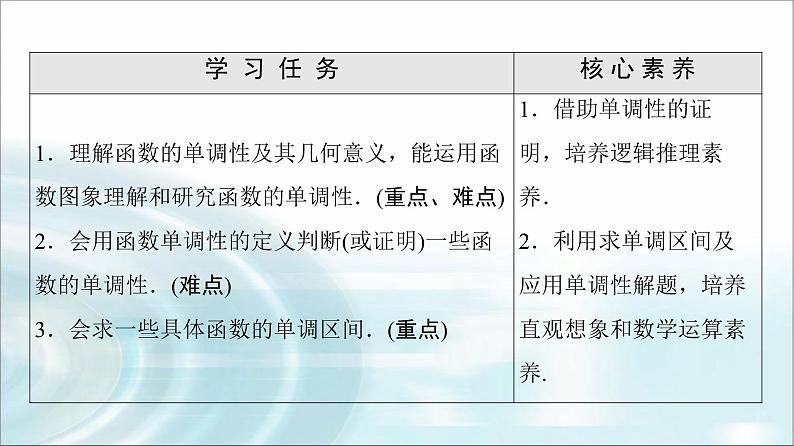




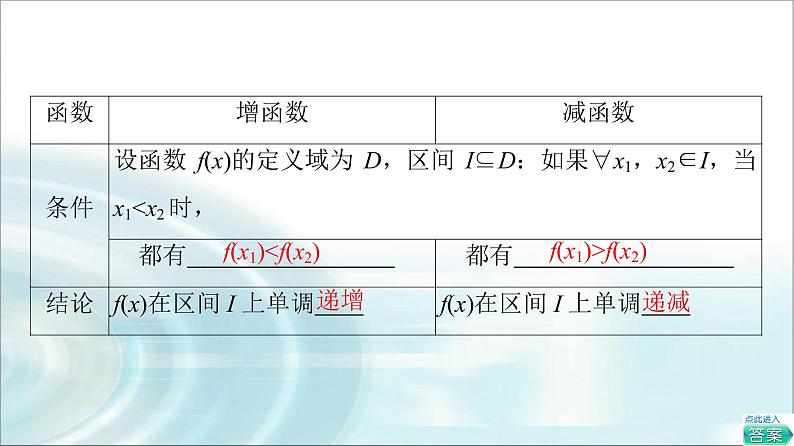






湘教版(2019)必修 第一册第3章 函数的概念与性质3.2 函数的基本性质课前预习课件ppt
展开课后素养落实(二十一) 函数的单调性
(建议用时:40分钟)
一、选择题
1.已知四个函数的图象如图所示,其中在定义域内具有单调性的函数是( )
A B C D
B [由图可知,选项B是定义域上的增函数,选项ACD不具有单调性.故选B.]
2.函数f(x)在R上是减函数,则有( )
A.f(3)<f(5) B.f(3)≤f(5)
C.f(3)>f(5) D.f(3)≥f(5)
C [∵3<5,且f(x)为R上的减函数,
∴f(3)>f(5).]
3.(多选题)下列函数在区间(0,+∞)上单调递增的是( )
A.y=2x+1 B.y=x2+1
C.y=3-x D.y=x2+2x+1
ABD [易知选项A,B,D在区间(0,+∞)上是单调递增的,C是减函数,故选ABD.]
4.若函数y=x2+(2a-1)x+1在区间(-∞,2]上单调递减,则实数a的取值范围是( )
A. B.
C.(3,+∞) D.(-∞,-3]
B [由题意可知-≥2,即a≤-,故选B.]
5.函数f(x)=|x|,g(x)=x(2-x)的递增区间依次是( )
A.(-∞,0],(-∞,1] B.(-∞,0],(1,+∞)
C.[0,+∞),(-∞,1] D.[0,+∞),[1,+∞)
C [分别作出f(x)与g(x)的图象(图略)得:f(x)在[0,+∞)上递增,g(x)在(-∞,1]上递增,故选C.]
二、填空题
6.如果二次函数f(x)=x2-(a-1)x+5在区间上单调递增,则实数a的取值范围为________.
(-∞,2] [∵函数f(x)=x2-(a-1)x+5的对称轴为x=且在区间上单调递增,
∴≤,即a≤2.]
7.若函数f(x)=在(a,+∞)上单调递减,则a的取值范围是________.
[-1,+∞) [函数f(x)=的单调递减区间为(-1,+∞),(-∞,-1),
又f(x)在(a,+∞)上单调递减,所以a≥-1.]
8.已知f(x)在定义域内是减函数,且f(x)>0,在其定义域内下列函数为单调增函数的是________.
①y=a+f(x)(a为常数);
②y=a-f(x)(a为常数);
③y=;④y=[f(x)]2.
②③ [f(x)在定义域内是减函数,且f(x)>0时,-f(x),均为增函数,故选②③.]
三、解答题
9.证明:函数y=在(-1,+∞)上单调递增.
[证明] 设x1>x2>-1,则
y1-y2=-=.
∵x1>x2>-1,∴x1-x2>0,x1+1>0,x2+1>0,
∴>0,即y1-y2>0,y1>y2,
∴y=在(-1,+∞)上单调递增.
10.若f(x)在区间(0,+∞)上单调递增,解不等式f(x)>f(8(x-2)).
[解] 由f(x)在(0,+∞)上单调递增得
解得2<x<.
1.若函数y=ax与y=-在(0,+∞)上都是单调递减的,则函数y=ax2+bx在(0,+∞)上( )
A.单调递增 B.单调递减
C.先增后减 D.先减后增
B [由于函数y=ax与y=-在(0,+∞)上均为减函数,故a<0,b<0,故二次函数f(x)=ax2+bx的图象开口向下,且对称轴为直线x=-<0,故函数y=ax2+bx在(0,+∞)上单调递减.]
2.(多选题)如果函数f(x)在区间[a,b]上单调递增,对于任意的x1,x2∈[a,b](x1≠x2),则下列结论中正确的是( )
A.>0
B.(x1-x2)[f(x1)-f(x2)]>0
C.f(a)≤f(x1)<f(x2)≤f(b)
D.f(x1)>f(x2)
AB [由函数单调性的定义可知,若函数y=f(x)在给定的区间上单调递增,则x1-x2与f(x1)-f(x2)同号,由此可知,选项A,B正确;对于选项C,D,因为x1,x2的大小关系无法判断,所以无法判断f(x1)与f(x2)的大小,故C,D不正确.]
3.已知函数f(x)=是R上的减函数,则实数a的取值范围是________.
(0,2] [依题意得实数a满足
解得0<a≤2.]
4.函数f(x)=2x2-3|x|的单调递减区间是________,单调递增区间是________.
和 和 [函数f(x)=2x2-3|x|=
图象如图所示,f(x)的单调递减区间为和;单调递增区间为和.
]
若f(x)在(0,+∞)上单调递增,且对一切x,y>0,满足f =f(x)-f(y).
(1)求f(1)的值;
(2)若f(6)=1,求不等式f(x+3)-f(2)<1的解集.
[解] (1)在f =f(x)-f(y)中,令x=y=1,则有f(1)=f(1)-f(1)=0,∴f(1)=0.
(2)∵f(6)=1,
∴f(x+3)-f(2)<1=f(6),
∴f <f(6).
∵f(x)在(0,+∞)上单调递增,
∴解得-3<x<9.
故不等式的解集为{x|-3<x<9}.
高中数学湘教版(2019)必修 第一册3.2 函数的基本性质课文配套课件ppt: 这是一份高中数学湘教版(2019)必修 第一册3.2 函数的基本性质课文配套课件ppt,文件包含湘教版高中数学必修第一册第3章32322第2课时奇偶性的应用课件ppt、湘教版高中数学必修第一册第3章32322第2课时奇偶性的应用学案doc、湘教版高中数学必修第一册课后素养落实24奇偶性的应用含答案doc等3份课件配套教学资源,其中PPT共41页, 欢迎下载使用。
湘教版(2019)必修 第一册3.2 函数的基本性质评课课件ppt: 这是一份湘教版(2019)必修 第一册3.2 函数的基本性质评课课件ppt,文件包含湘教版高中数学必修第一册第3章32322第1课时奇偶性的概念课件ppt、湘教版高中数学必修第一册第3章32322第1课时奇偶性的概念学案doc、湘教版高中数学必修第一册课后素养落实23奇偶性的概念含答案doc等3份课件配套教学资源,其中PPT共44页, 欢迎下载使用。
湘教版(2019)3.2 函数的基本性质图文ppt课件: 这是一份湘教版(2019)3.2 函数的基本性质图文ppt课件,文件包含湘教版高中数学必修第一册第3章32321第2课时函数的最大小值课件ppt、湘教版高中数学必修第一册第3章32321第2课时函数的最大小值学案doc、湘教版高中数学必修第一册课后素养落实22函数的最大小值含答案doc等3份课件配套教学资源,其中PPT共42页, 欢迎下载使用。













