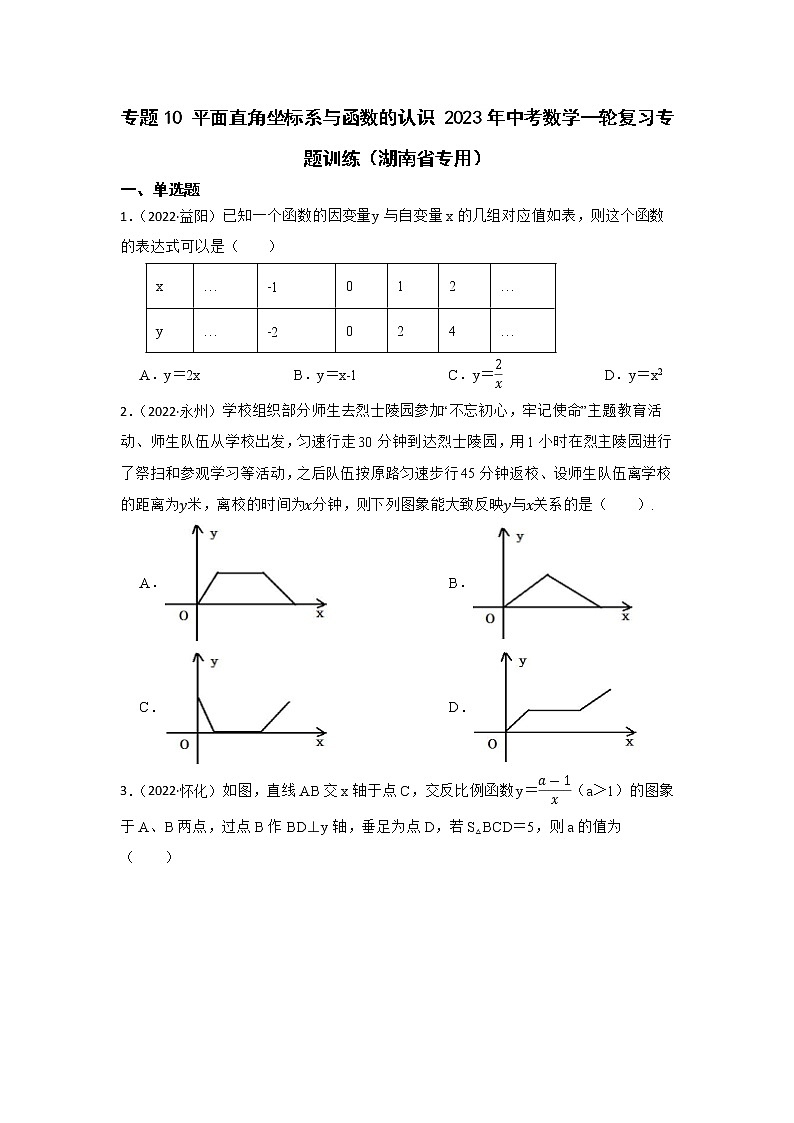

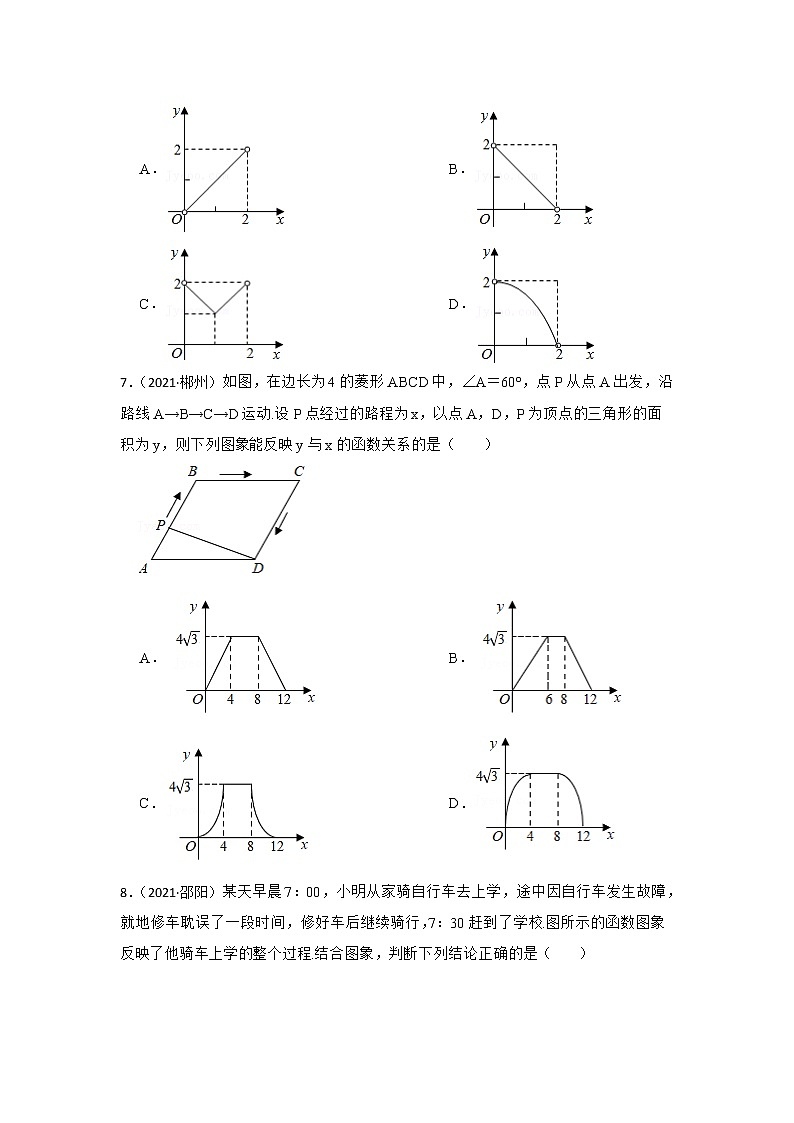
专题10 平面直角坐标系与函数的认识 2023年中考数学一轮复习专题训练(湖南省专用)
展开专题10 平面直角坐标系与函数的认识 2023年中考数学一轮复习专题训练(湖南省专用)
一、单选题
1.(2022·益阳)已知一个函数的因变量y与自变量x的几组对应值如表,则这个函数的表达式可以是( )
x
…
﹣1
0
1
2
…
y
…
﹣2
0
2
4
…
A.y=2x B.y=x﹣1 C.y=2x D.y=x2
2.(2022·永州)学校组织部分师生去烈士陵园参加“不忘初心,牢记使命”主题教育活动、师生队伍从学校出发,匀速行走30分钟到达烈士陵园,用1小时在烈主陵园进行了祭扫和参观学习等活动,之后队伍按原路匀速步行45分钟返校、设师生队伍离学校的距离为y米,离校的时间为x分钟,则下列图象能大致反映y与x关系的是( ).
A. B.
C. D.
3.(2022·怀化)如图,直线AB交x轴于点C,交反比例函数y=a-1x(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( )
A.8 B.9 C.10 D.11
4.(2022·邵阳)如图是反比例函数y=1x的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )
A.1 B.12 C.2 D.32
5.(2021·湘西)已知点 M(x,y) 在第一象限,且 x+y=12 ,点 A(10,0) 在 x 轴上,当 ΔOMA 为直角三角形时,点 M 的坐标为( )
A.(10,2) , (8,4) 或 (6,6) B.(8,4) , (9,3) 或 (5,7)
C.(8,4) , (9,3) 或 (10,2) D.(10,2) , (9,3) 或 (7,5)
6.(2021·南县)如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是( )
A. B.
C. D.
7.(2021·郴州)如图,在边长为4的菱形ABCD中,∠A=60°,点P从点A出发,沿路线A→B→C→D运动.设P点经过的路程为x,以点A,D,P为顶点的三角形的面积为y,则下列图象能反映y与x的函数关系的是( )
A. B.
C. D.
8.(2021·邵阳)某天早晨7:00,小明从家骑自行车去上学,途中因自行车发生故障,就地修车耽误了一段时间,修好车后继续骑行,7:30赶到了学校.图所示的函数图象反映了他骑车上学的整个过程.结合图象,判断下列结论正确的是( )
A.小明修车花了15min
B.小明家距离学校1100m
C.小明修好车后花了30min到达学校
D.小明修好车后骑行到学校的平均速度是3m/s
9.(2021·攸县模拟)在平面直角坐标系中,点 P(1-a,a-3) 在第三象限内,则a的取值范围是( )
A.a>1 B.a<3 C.1
10.(2021·长沙模拟)如图,将线段 AB 平移到线段 CD 的位置,则a-b的值为( )
A.4 B.0 C.3 D.-5
二、填空题
11.(2022·娄底)函数y=1x-1的自变量x的取值范围是 .
12.(2021·怀化)如图,在平面直角坐标系中,已知 A(-2,1) , B(-1,4) , C(-1,1) ,将 △ABC 先向右平移3个单位长度得到 △A1B1C1 ,再绕 C1 顺时针方向旋转 90° 得到 △A2B2C1 ,则 A2 的坐标是 .
13.(2021·衡阳)如图1,菱形 ABCD 的对角线 AC 与 BD 相交于点O,P、Q两点同时从O点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P的运动路线为 O-A-D-O ,点Q的运动路线为 O-C-B-O .设运动的时间为x秒,P、Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,当点P在 A-D 段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为 厘米.
14.(2021·长沙模拟)如图,一次函数y=k1x+b的图象与反比例函数y= k2x 的图象相交于A(2,3),B(6,1)两点,当k1x+b< k2x 时,x的取值范围为 .
15.(2021·长沙模拟)在平面直角坐标系中,矩形 ABCD 的位置如图所示,其中 B(-1,-1), AB=3,BC=4 , AB//y 轴,则顶点D的坐标为 .
16.(2021·岳阳模拟)若点P(2k+1,1﹣k)在第一象限,则k的取值范围是 .
17.(2021·岳阳模拟)函数y= 2x-5 的自变量x的取值范围为 .
18.(2021·蒸湘模拟)如图,在平面直角坐标系中,等腰直角三角形OAA1 的直角边 OA 在 x 轴上,点 A1 在第一象限,且 OA=1 ,以点 A1 为直角顶点, OA1 为直角边作等腰直角三角形 OA1A2 ,再以点 A2 为直角顶点, OA2 为直角边作等腰直角三角形 OA2A3 ……以此规律,则点 A2018 的坐标是 .
19.(2022九上·岳麓开学考)如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,y的值为 .
20.(2022七下·雨花期末)如图,∠AOC=30°,∠BOC=150°,OD为∠BOA的平分线,若A点可表示为(2,30°),B点可表示为(4,150°),则D点可表示为 .
三、综合题
21.(2022·湘潭)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣4,0),C(﹣2,2),将△ABC绕原点O顺时针旋转90°后得到△A1B1C1.
(1)请写出A1、B1、C1三点的坐标:
A1 ,B1 ,C1 ;
(2)求点B旋转到点B1的弧长.
22.(2022·株洲)如图所示,在平面直角坐标系Oxy中,点A、B分别在函数y1=2x(x<0)、y2=kx(x>0,k>0)的图象上,点C在第二象限内,AC⊥x轴于点P,BC⊥y轴于点Q,连接AB、PQ,已知点A的纵坐标为-2.
(1)求点A的横坐标;
(2)记四边形APQB的面积为S,若点B的横坐标为2,试用含k的代数式表示S.
23.(2021·郴州)某商店从厂家以每件2元的价格购进一批商品,在市场试销中发现,此商品的月销售量y(单位:万件)与销售单价x(单位元)之间有如下表所示关系:
x
…
4.0
5.0
5.5
6.5
7.5
…
y
…
8.0
6.0
5.0
3.0
1.0
…
(1)根据表中的数据,在如图中描出实数对(x,y)所对应的点,并画出y关于x的函数图象;
(2)根据画出的函数图象,求出y关于x的函数表达式;
(3)设经营此商品的月销售利润为P(单位:万元),
①写出P关于x的函数表达式;
②该商店计划从这批商品获得的月销售利润为10万元(不计其它成本),若物价局限定商品的销售单价不得超过进价的200%,则此时的销售单价应定为多少元?
24.(2021·张家界模拟)问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
(1)(应用):
①若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
②若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
(2)(拓展):
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
①如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F) ;
②如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= .
③如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= .
25.(2021·蒸湘模拟)某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第5分钟起每分钟每毫升血液中含药量增加0.2微克,第100分钟达到最高,接着开始衰退.血液中含药量y (微克)与时间 x (分钟)的函数关系如图.并发现衰退时 y 与 x 成反比例函数关系.
(1)a= ;
(2)当5⩽x⩽100 时, y 与 x 之间的函数关系式为 ;当x>100 时, y 与 x 之间的函数关系式为 ;
(3)如果每毫升血液中含药量不低于10微克时是有效的,求出一次服药后的有效时间多久?
答案解析部分
1.【答案】A
【解析】【解答】解:∵当x=-1时y=-1×2=-2;
当x=1时y=1×2=2;
当x=2时y=2×2=4 …
∴y与x的表达式为y=2x.
故答案为:A.
【分析】观察表中每一组x,y的对应值,可知y是x的2倍,可得答案.
2.【答案】A
【解析】【解答】解:∵师生队伍从学校出发,匀速行走30分钟到达烈士陵园,
∴当0≤x≤30时,y随x的增大而增大;
∵用1小时在烈主陵园进行了祭扫和参观学习等活动
∴当30<x≤90时,y是一个定值;
∵之后队伍按原路匀速步行45分钟返校,
当90<x≤135时,y随x的增大而减小;
∴能大致反映y与x关系的是A,
故答案为:A.
【分析】抓住已知条件:师生队伍从学校出发,匀速行走30分钟到达烈士陵园,可知y随x的增大而增大;用1小时在烈主陵园进行了祭扫和参观学习等活动,此时y是一个定值;之后队伍按原路匀速步行45分钟返校,可知y随x的增大而减小;据此可得答案.
3.【答案】D
【解析】【解答】解:设B(m,a-1m),
∵BD⊥y轴
∴S△BCD=12m⋅a-1m=5,
解得:a=11
故答案为:D.
【分析】设B(m,a-1m),则BD=m,△BCD的边BD上的高线为a-1m,接下来根据三角形的面积公式就可求出a的值.
4.【答案】B
【解析】【解答】解:设A(x,y),则OB=x,AB=y,
∵A为反比例函数y=1x图象上一点,
∴xy=1,
∴S△ABO=12AB•OB=12xy=12×1=12.
故答案为:B.
【分析】设A(x,y),则OB=x,AB=y,根据点A在反比例函数图象上可得xy=1,由三角形的面积公式可得S△ABO=12xy,据此计算.
5.【答案】C
【解析】【解答】解:由题意得:
当 ∠OAM=90° 时,如图所示:
∵A(10,0) , M(x,y) ,
∴x=10 ,
∵x+y=12 ,
∴y=2 ,
∴M(10,2) ;
当 ∠OMA=90° 时,过点M作MB⊥x轴于点B,如图所示:
∴∠MBO=∠MBA=∠OMA=90° ,
∴△MBO∽△ABM ,
∴BMAB=OBBM ,即 BM2=OB⋅AB ,
∵A(10,0) , M(x,y) ,
∴OB=x,BM=y,OA=10 ,
∵x+y=12 ,
∴OB=x,BM=12-x,AB=10-x ,
∴(12-x)2=x⋅(10-x) ,解得: x1=8,x2=9 ,
∴当 x=8 时,则 y=4 ;当 x=9 时,则 y=3 ,
∴M(8,4) 或 M(9,3) ;
故答案为:C.
【分析】根据题意分两种情况:①当 ∠OAM=90° 时,②当∠OMA=90°时,据此分别求解即可.
6.【答案】B
【解析】【解答】解:∵▱ABCD的面积为4,
∴当x=0时,y=2;x=2时,y=0;
∵△BPC的底边AP边上的高不变,
∴y是x的一次函数,
故只有选项B符合题意.
故答案为:B.
【分析】根据平行四边形的面积可得:当x=0时,y=2;x=2时,y=0,由图形可得△BPC的底边AP边上的高不变,据此判断.
7.【答案】A
【解析】【解答】解:过点B作BE⊥AD于点 E,如图所示:
边长为4的菱形,ABCD中,∠A=60°,
∴AB=AD=BC=4,
∴∠ABE=30°,
∴AE=2,BE=2 3 ,
当点P从点A运动到点B时,过点P作PF⊥AD于点F,
则AP=x,AF= 12 x,PF= 32 x,
S△ADP= 12 •AD•PF= 12×4 • 32 x= 3 x,
∴△ADP的面积逐渐增大;
当在线段BC上时,
S△ADP= 12 •AD•BE= 12×4 ×2 3 =4 3 ,
∴△ADP的面积保持不变;
当点P在线段CD上时,如图,过点P作PM⊥AD交AD的延长线于点M,
则AB+BC+CP=x,
则DP=12﹣x,DM=6﹣ 12 x,PM= 3 DM=6 3 ﹣ 32 x,
S△ADP= 12 •AD•PM= 12×4 ×(6 3 ﹣ 32 x)=12 3 ﹣ 3 x,
∴△ADP的面积逐渐减小.
故答案为:A.
【分析】过点B作BE⊥AD于点 E,由菱形的性质可得AB=AD=BC=4,由直角三角形两锐角互余的性质可得∠ABE=30°,据此可得AE、BE的值;当点P从点A运动到点B时,过点P作PF⊥AD于点F,则AP=x,AF=12x,PF=32x,然后表示出S△ADP;当在线段BC上时,由三角形的面积公式可得S△ADP;
当点P在线段CD上时,如图,过点P作PM⊥AD交AD的延长线于点M,则AB+BC+CP=x,DP=12﹣x,DM=6-12x,PM=3DM=6 3﹣32x,表示出S△ADP,据此判断.
8.【答案】A
【解析】【解答】解:根据图象7:05-7:20为修车时间20-5=15分钟,故A正确;
小明家距离学校2100m,故B错误;
小明修好车后花了30-20=10分钟到达学校,故C错误;
小明修好车后骑行到学校的平均速度是(2100-1000)÷600= 116 m/s,故D错误;
故答案为:A.
【分析】由于时间在变,而路程不变,根据横坐标即可求出时间;根据图象的纵坐标,求出小明家距离学校的路程;利用小明修好车后的路程除以时间即得小明修好车后骑行到学校的平均速度,然后判断即可.
9.【答案】C
【解析】【解答】解:∵点 P(1-a,a-3) 在第三象限,
∴1-a<0①a-3<0② ,
解不等式①,得:a>1,
解不等式②,得:a<3,
则 1
【分析】先根据第三象限内点的坐标符号特点得出关于a的不等式组,解之即可.
10.【答案】B
【解析】【解答】解:由题意,线段AB向左平移3个单位,再向上平移4个单位得到线段CD,
∴a=5-3=2,b=-2+4=2,
∴a-b=0,
故答案为:B.
【分析】看图,根据平移的过程,列式分别求出a、b值,然后代值计算即可.
11.【答案】x>1
【解析】【解答】解:由1x-1有意义可得:
x-1≥0x-1≠0, 即x-1>0,
解得:x>1
故答案为:x>1.
【分析】根据分式的分母不能为0及二次根式的被开方数不能为负数可得x-1>0,求解即可.
12.【答案】(2,2)
【解析】【解答】解:如图示: △A1B1C1 , △A2B2C1 为所求,
根据图象可知, A2 的坐标是(2,2),
故答案是:(2,2).
【分析】利用平移的性质和旋转的性质,画出△A2B2C1,即可得到点A2的坐标.
13.【答案】(23+3)
【解析】【解答】解:由图可知, AC=23,BD=2 (厘米),
∵四边形 ABCD 为菱形
∴OC=12AC=3,OB=12BD=1 (厘米)
∴∠ACB=30°
P在 AD 上时,Q在 BC 上, PQ 距离最短时, PQ 连线过O点且垂直于 BC .
此时,P、Q两点运动路程之和 S=2(OC+CQ)
∵CQ=OC⋅cos∠ACB=3×32=32 (厘米)
∴S=2(3+32)=23+3 (厘米)
故答案为 (23+3) .
【分析】由图象可知当点P运动到A点,点Q运动到C点时,即得AC=23,BD=2,由菱形的性质得出OC=12AC=3,OB=12BD=1,从而得出∠ACB=30°,由题意可得P在 AD 上时,Q在 BC 上, PQ 距离最短时, PQ 连线过O点且垂直于 BC .此时,P、Q两点运动路程之和 S=2(OC+CQ),据此求出结论即可.
14.【答案】0<x<2或x>6
【解析】【解答】解:由图象可知,当k1x+b< k2x 时,x的取值范围为0<x<2或x>6.
故答案为0<x<2或x>6.
【分析】根据题意,看图象,找出直线在双曲线以下的部分时x的取值范围即可.
15.【答案】(3,2)
【解析】【解答】解: ∵ 四边形ABCD是矩形,
∴AB=CD=3,CB=AD=4,AD//BC,AB//CD ,
且 AB//y 轴,
∴AD//BC//x 轴, AB//CD//y 轴,
∵B(-1,-1),AB=3,BC=4 ,
∴ 点C横坐标为3,点A纵坐标为2,
∴ 点D坐标为(3,2).
故答案为:(3,2).
【分析】由矩形的性质可得AB=CD=3,BC=AD=4,AD∥BC,AB∥CD,然后根据点B的坐标以及AB、BC的值可得点C的横坐标,点A的纵坐标,据此不难得到点D的坐标.
16.【答案】﹣ 12 <k<1
【解析】【解答】解:∵点P(2k+1,1﹣k)在第一象限,
∴2k+1>0①1-k>0② ,
解不等式①得,k>﹣ 12 ,
解不等式②得,k<1,
所以,不等式组的解集是﹣ 12 <k<1.
故答案为:﹣ 12 <k<1.
【分析】根据第一象限内点的横坐标与纵坐标都是正数列出不等式组求解即可.
17.【答案】x≠5
【解析】【解答】解:根据分式有意义的条件,得:x-5≠0,即x≠5;故答案为x≠5.
【分析】根据分式有意义的条件,即可快速作答.
18.【答案】(0, 21009)
【解析】【解答】解:由已知可得,点A每次旋转转动45°,则转动一周需要8次变换,每次转动点A到原点的距离均为前一次的2倍,即OAn=2OAn-1,
∵2018=252×8+2,
∴点A2018落在y轴的正半轴上,
又∵OA2018=(2)2018=21009,
∴A2018(0,21009).
故答案为:(0,21009).
【分析】通过已知条件,结合图形变换可知点A每次旋转转动45°,则转动一周需要8次变换,每次转动点A到原点的距离均为前一次的 2倍,即OAn=2OAn-1,再由2018=252×8+2可得点A2018落在y轴的正半轴上,再由OA2018=(2)2018=21009,即可求得A2018的坐标.
19.【答案】10
【解析】【解答】解: ∵x=4 时,即R从N到达点P时,面积开始不变,
∴PN=4 ,
同理可得 QP=5 ,
∴ 当 x=9 时,点R运动到点Q处,
∴y=12PN⋅PQ=12×4×5=10 .
故答案为:10.
【分析】根据图形可得PN=4,QP=5,故当x=9时,点R运动到点Q处,然后根据三角形的面积公式进行计算.
20.【答案】(5,90°)
【解析】【解答】解:∵∠BOC=150°,∠AOC=30°,
∴∠AOB=120°,
∵OD为∠BOA的平分线,
∴∠AOD=∠BOD=60°,
∴∠DOC=∠AOD+∠AOC=60°+30°=90°,
∵A点可表示为(2,30°),B点可表示为(4,150°),
∴D点可表示为:(5,90°).
故答案为:(5,90°).
【分析】由∠AOB=∠BOC-∠AOC可得∠AOB的度数,根据角平分线的概念得∠AOD=∠BOD=60°,进而由∠DOC=∠AOD+∠AOC求出∠DOC的度数,据此可得点D的坐标.
21.【答案】(1)(1,1);(0,4);(2,2)
(2)解:由图知点B旋转到点B的弧长所对的圆心角是90°,OB=4,
点B旋转到点B的弧长=90π×4180=2π.
【解析】【解答】解:(1) 将△ABC绕原点O顺时针旋转90°后得到△A1B1C1 ,则 A1 (1,1), B1 (0,4), C1 (2,2);
【分析】(1)将△ABC绕着点O按顺时针方向旋转90°得到△A1B1C1 ,在坐标系中读出A1 , B1 , C1 点的坐标即可;
(2)由图知点B旋转到点B的弧长所对的圆心角是90°,且OB=4, 根据弧长公式计算即可求出结果.
22.【答案】(1)解:将y=-2代入y1=2x(x<0)中,
-2=2x,解得:x=-1,
∴A(-1,-2).
(2)解:由题意可得B(2,k2),
∵AC⊥x轴,BC⊥y轴,
∴C(-1,k2),
∴S=SΔABC-SΔPCQ
=12AC⋅BC-12PC⋅CQ
=12(2+k2)(2+1)-12×k2×1
=3+3k4-k4
=3+k2.
【解析】【分析】(1)将y=-2代入y1=2x中求出x的值,据此可得点A的坐标;
(2) 由题意可得B(2,k2),则C(-1,k2),然后根据S=S△ABC-S△PCQ进行解答.
23.【答案】(1)解:如图
(2)解:根据图象设y=kx+b,把(4.0,8.0)和(5.0,6.0)代入上式,
得 8.0=4.0k+b6.0=5.0k+b ,
解得 k=-2b=16 ,
∴y=﹣2x+16,
∵y≥0,
∴﹣2x+16≥0,
解得x≤8,
∴y关于x的函数表达式为y=﹣2x+16(x≤8)
(3)解:①P=(x﹣2)y
=(x﹣2)(﹣2x+16)
=﹣2x²+20x﹣32,
即P与x的函数表达式为:P=﹣2x²+20x﹣32(x≤8);
②∵物价局限定商品的销售单价不得超过进价的200%,
∴x≤2×200%,
即x≤4,
由题意得P=10,
∴﹣2x²+20x﹣32=10,
解得x1=3,x2=7,
∵x≤4,
∴此时销售单价为3元.
【解析】【分析】(1)根据描点、连线可作出函数图象;
(2)设y=kx+b,将(4.0,8.0)、(5.0,6.0)代入可得k、b的值,据此可得函数表达式;
(3)①P=(x-2)y,将(2)中的表达式代入化简即可;
②由题意可得x≤2×200%,即x≤4,然后令p=10求出x的值即可.
24.【答案】(1)3;(1,2)或(1,﹣2)
(2)=5;2或﹣2;4或8
【解析】【解答】解:(1)(应用):
①AB的长度为|﹣1﹣2|=3.
故答案为:3;
②由CD∥y轴,可设点D的坐标为(1,m),
∵CD=2,
∴|0﹣m|=2,解得:m=±2,
∴点D的坐标为(1,2)或(1,﹣2).
故答案为:(1,2)或(1,﹣2);
(2)(拓展):
①d(E,F)=|2﹣(﹣1)|+|0﹣(﹣2)|=5.
故答案为:=5;
②∵E(2,0),H(1,t),d(E,H)=3,
∴|2﹣1|+|0﹣t|=3,解得:t=±2.
故答案为:2或﹣2;
③由点Q在x轴上,可设点Q的坐标为(x,0),
∵三角形OPQ的面积为3,
∴12 |x|×3=3,解得:x=±2.
当点Q的坐标为(2,0)时,d(P,Q)=|3﹣2|+|3﹣0|=4;
当点Q的坐标为(﹣2,0)时,d(P,Q)=|3﹣(﹣2)|+|3﹣0|=8.
故答案为:4或8.
【分析】(1)①根据平行于x轴的直线上任意两点的距离等于这两点的横坐标差的绝对值可得结果;②根据平行于y轴的直线上所有点的横坐标相同及平行于y轴的直线上任意两点的距离等于这两点的纵坐标差的绝对值可得结果;
(2)①根据折线距离公式可得结果;②根据折现公式可得关于t的含绝对值方程,求解即可;③由点Q在x轴上,可设点Q的坐标为(x,0),根据面积可得x的值,再根据折线距离可得结果.
25.【答案】(1)19
(2)y=0.2x-1;y=1900x
(3)解:令 y=0.2x-1=10 解得: x=55 ,
令 y=1900x=10 ,解得: x=190
∴190-55=135 分钟,
∴ 服药后能持续135分钟.
【解析】【解答】解:(1)a=0.2×( 100-5)=19(微克).
故答案为:19.
(2)当 5⩽x⩽100时,设 y 与 x 之间的函数关系式为 y=k1x+b
∵ 经过点 (5,0) , (100,19)
∴5k+b=0100k+b=19,解得: k=0.2b=-1,
∴ 解析式为 y=0.2x-1 ;
当 x>100 时, y 与 x 之间的函数关系式为 y=kx ,
∵ 经过点 (100,19) ,
∴k100=19
解得: k=1900 ,
∴ 函数的解析式为 y=1900x ;
【分析】(1)根据第5分钟起,每分钟血液中含药量增加0.2微克,即增加的速度,则在100分钟时增加的药量为0.2×(100-5),即可求出a值;
(2)当5≤x≤100时,设函数关系式为y=k1x+b,将点(5,0)和(100,19)代入解析式,建立方程组 5k+b=0100k+b=19,解得 k=0.2b=-1,即y=0.2x-1;当x>100时,设函数关系式为y= kx,将点(100,19),得k=1900,即y= 1900x;
(3)由(2)中求出的不同时间段的函数关系式得,当y=0.2x-1=10,解得x=55,当y= 1900x=10,解得x=190,由190-55即可求得一次服药后的有效时间
专题12 平面直角坐标系和函数的认识 山东省2023年中考数学一轮复习专题训练: 这是一份专题12 平面直角坐标系和函数的认识 山东省2023年中考数学一轮复习专题训练,共22页。试卷主要包含了单选题,填空题等内容,欢迎下载使用。
第8讲 平面直角坐标系和函数的认识 2023年中考数学一轮复习专题训练(江苏专用): 这是一份第8讲 平面直角坐标系和函数的认识 2023年中考数学一轮复习专题训练(江苏专用),共20页。试卷主要包含了单选题,填空题,综合题等内容,欢迎下载使用。
专题1 实数 2023年中考数学一轮复习专题训练(湖南省专用): 这是一份专题1 实数 2023年中考数学一轮复习专题训练(湖南省专用),共9页。试卷主要包含了单选题,填空题,计算题等内容,欢迎下载使用。













