专题15 三角形 2023年中考数学一轮复习专题训练（湖南省专用）

这是一份专题15 三角形 2023年中考数学一轮复习专题训练（湖南省专用），共33页。试卷主要包含了单选题，填空题，综合题等内容，欢迎下载使用。

专题15 三角形 2023年中考数学一轮复习专题训练（湖南省专用）
一、单选题
1．（2022·岳阳）下列命题是真命题的是（　　）
A．对顶角相等
B．平行四边形的对角线互相垂直
C．三角形的内心是它的三条边的垂直平分线的交点
D．三角分别相等的两个三角形是全等三角形
2．（2022·湘西）如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DH⊥AB于点H，连接OH，OH＝4，若菱形ABCD的面积为323，则CD的长为（　　）

A．4 B．43 C．8 D．83
3．（2022·常德）如图，在Rt△ABC中，∠ABC=90°，∠ACB=30°，将△ABC绕点C顺时针旋转60°得到△DEC，点A、B的对应点分别是D，E，点F是边AC的中点，连接BF，BE，FD.则下列结论错误的是（　　）

A．BE=BC B．BF∥DE，BF=DE
C．∠DFC=90° D．DG=3GF
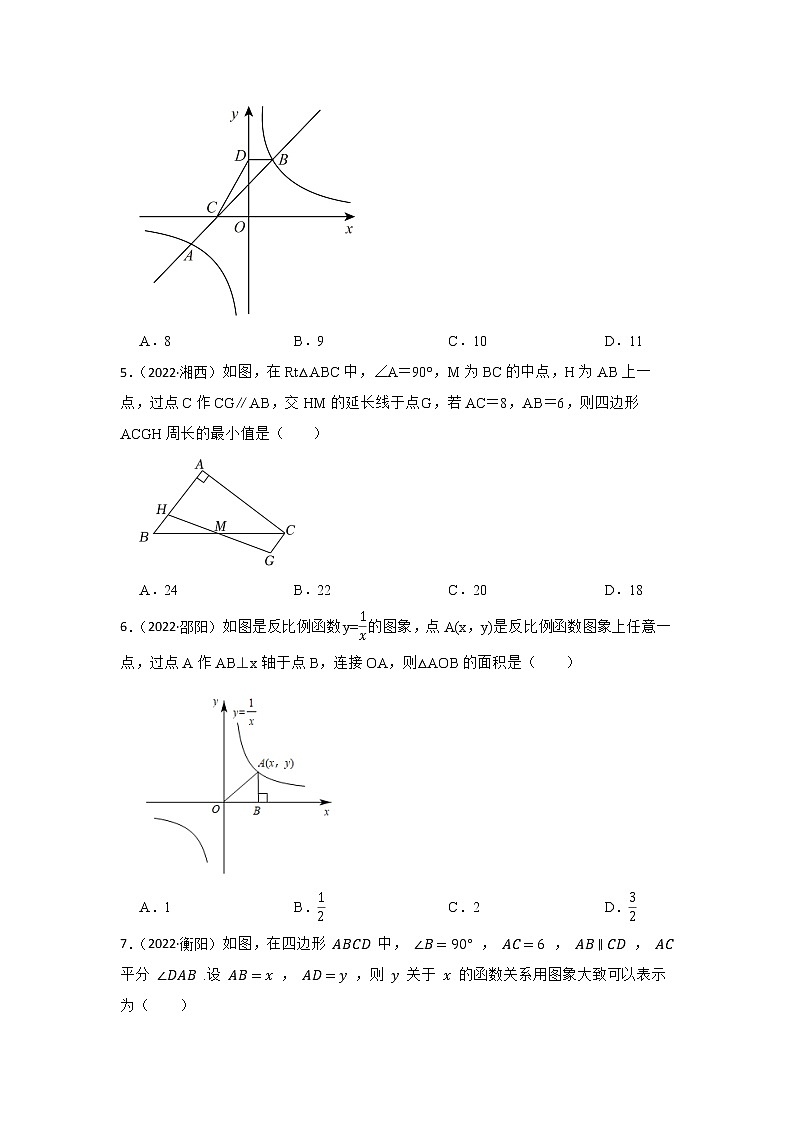
4．（2022·怀化）如图，直线AB交x轴于点C，交反比例函数y＝a-1x（a＞1）的图象于A、B两点，过点B作BD⊥y轴，垂足为点D，若S△BCD＝5，则a的值为（　　）

A．8 B．9 C．10 D．11
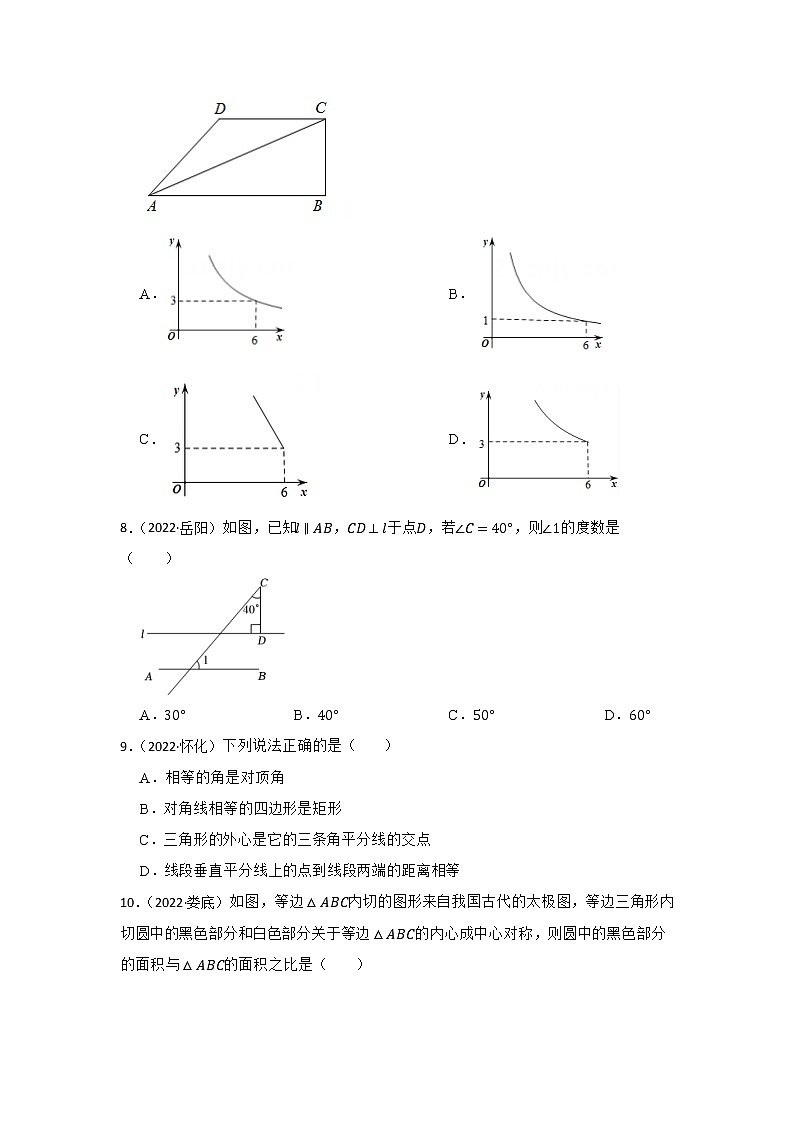
5．（2022·湘西）如图，在Rt△ABC中，∠A＝90°，M为BC的中点，H为AB上一点，过点C作CG∥AB，交HM的延长线于点G，若AC＝8，AB＝6，则四边形ACGH周长的最小值是（　　）

A．24 B．22 C．20 D．18
6．（2022·邵阳）如图是反比例函数y=1x的图象，点A(x，y)是反比例函数图象上任意一点，过点A作AB⊥x轴于点B，连接OA，则△AOB的面积是（　　）

A．1 B．12 C．2 D．32
7．（2022·衡阳）如图，在四边形 ABCD 中， ∠B=90° ， AC=6 ， AB∥CD ， AC 平分 ∠DAB .设 AB=x ， AD=y ，则 y 关于 x 的函数关系用图象大致可以表示为（　　）

A． B．
C． D．
8．（2022·岳阳）如图，已知l∥AB，CD⊥l于点D，若∠C=40°，则∠1的度数是（　　）

A．30° B．40° C．50° D．60°
9．（2022·怀化）下列说法正确的是（　　）
A．相等的角是对顶角
B．对角线相等的四边形是矩形
C．三角形的外心是它的三条角平分线的交点
D．线段垂直平分线上的点到线段两端的距离相等
10．（2022·娄底）如图，等边△ABC内切的图形来自我国古代的太极图，等边三角形内切圆中的黑色部分和白色部分关于等边△ABC的内心成中心对称，则圆中的黑色部分的面积与△ABC的面积之比是（　　）

A．3π18 B．318 C．3π9 D．39
二、填空题
11．（2022·邵阳）如图，在等腰△ABC中，∠A=120°，顶点B在▱ODEF的边DE上，已知∠1=40°，则∠2=　 　.

12．（2022·邵阳）已知矩形的一边长为6cm，一条对角线的长为10cm，则矩形的面积为　 　cm2.
13．（2022·娄底）如图，已知等腰△ABC的顶角∠BAC的大小为θ，点D为边BC上的动点（与B、C不重合），将AD绕点A沿顺时针方向旋转θ角度时点D落在D'处，连接BD'.给出下列结论：①△ACD≅△ABD'；②△ACB∼△ADD'；③当BD=CD时，△ADD'的面积取得最小值.其中正确的结论有　 　（填结论对应的序号）.

14．（2022·常德）如图，已知F是△ABC内的一点，FD∥BC，FE∥AB，若▱BDFE的面积为2，BD=13BA，BE=14BC，则△ABC的面积是　 　.

15．（2022·岳阳）如图，在△ABC中，AB=AC，AD⊥BC于点D，若BC=6，则CD=　 　.

16．（2022·湘潭）如图，一束光沿CD方向，先后经过平面镜OB、OA反射后，沿EF方向射出，已知∠AOB=120°，∠CDB=20°，则∠AEF=　 　

17．（2022·岳阳）如图，在⊙O中，AB为直径，AB=8，BD为弦，过点A的切线与BD的延长线交于点C，E为线段BD上一点（不与点B重合），且OE=DE.

（1）若∠B=35°，则AD的长为　 　（结果保留π）；
（2）若AC=6，则DEBE=　 　.
18．（2022·衡阳）如图，在 △ABC 中，分别以点 A 和点 B 为圆心，大于 12AB 的长为半径作圆弧，两弧相交于点 M 和点 N ，作直线 MN 交 CB 于点 D ，连接 AD .若 AC=8 ， BC=15 ，则 △ACD 的周长为　 　.

19．（2022·株洲）如图所示，已知∠MON=60°，正五边形ABCDE的顶点A、B在射线OM上，顶点E在射线ON上，则∠AEO=　 　度.

20．（2022·衡阳模拟）如图，△OA1B1，△A1A2B2，△A2A3B3，…，△An﹣1AnBn都是斜边在x轴上的等腰直角三角形，点A1，A2，A3，…，An都在x轴上，点B1，B2，B3，…，Bn都在反比例函数y＝1x（x＞0）的图象上，则点Bn的坐标为　 　.（用含有正整数n的式子表示）

三、综合题
21．（2022·湘西）如图，在矩形ABCD中，E为AB的中点，连接CE并延长，交DA的延长线于点F．

（1）求证：△AEF≌△BEC．
（2）若CD＝4，∠F＝30°，求CF的长．
22．（2022·湘西）如图，在Rt△ABC中，∠B＝90°，AE平分∠BAC交BC于点E，O为AC上一点，经过点A、E的⊙O分别交AB、AC于点D、F，连接OD交AE于点M．

（1）求证：BC是⊙O的切线．
（2）若CF＝2，sinC＝35，求AE的长．
23．（2022·常德）如图，已知AB是⊙O的直径，BC⊥AB于B，E是OA上的一点，ED∥BC交⊙O于D，OC∥AD，连接AC交ED于F.

（1）求证：CD是⊙O的切线；
（2）若AB=8，AE=1，求ED、EF的长.
24．（2022·岳阳）如图，反比例函数y=kx(k≠0)与正比例函数y=mx(m≠0)的图象交于点A(-1，2)和点B，点C是点A关于y轴的对称点，连接AC，BC.

（1）求该反比例函数的解析式；
（2）求△ABC的面积；
（3）请结合函数图象，直接写出不等式kx 25．（2022·湘潭）在△ABC中，∠BAC=90°，AB=AC，直线l经过点A，过点B、C分别作l的垂线，垂足分别为点D、E.

（1）特例体验：如图①，若直线l∥BC，AB=AC= 2 ，分别求出线设BD、CE和DE的长；
（2）规律探究：
（Ⅰ）如图②，若直线l从图①状态开始绕点A旋转α（0＜α＜45°），请探究线段BD、CE和DE的数量关系并说明理由；
（Ⅱ）如图③，若直线l从图①状态开始绕点A顺时针旋转α（45°＜α＜90°），与线段BC相交于点H，请再探线段BD、CE和DE的数量关系并说明理由；
（3）尝试应用：在图③中，延长线设BD交线段AC于点F，若CE=3，DE=1，求S△BFC．
26．（2022·郴州）如图，在 △ABC 中， AB=AC .以AB为直径的 ⊙O 与线段BC交于点D，过点D作 DE⊥AC ，垂足为E，ED的延长线与AB的延长线交于点P.

（1）求证：直线PE是 ⊙O 的切线；
（2）若 ⊙O 的半径为6， ∠P=30° ，求CE的长.
27．（2022·娄底）如图，已知BD是Rt△ABC的角平分线，点O是斜边AB上的动点，以点O为圆心，OB长为半径的⊙O经过点D，与OA相交于点E.

（1）判定AC与⊙O的位置关系，为什么？
（2）若BC=3，CD=32，
①求sin∠DBC、sin∠ABC的值；
②试用sin∠DBC和cos∠DBC表示sin∠ABC，猜测sin2α与sinα，cosα的关系，并用α=30°给予验证.

答案解析部分
1．【答案】A
【解析】【解答】解：A、对顶角相等是一个正确的命题，是真命题，故A选项符合题意；
B、菱形的对角线互相垂直，非菱形的平行四边形的对角线不垂直，所以平行四边形的对角线互相垂直是一个假命题，故B选项不符合题意；
C、三角形的内心是三角形内角平分线的交点，不一定是三边的垂直平分线的交点，则三角形的内心是它的三条边的垂直平分线的交点是一个假命题，故C选项不符合题意；
D、三角分别相等的两个三角形不一定全等，故D选项不符合题意.
故答案为：A.
【分析】根据对顶角的性质可判断A；根据平行四边形的性质可判断B；根据内心的概念可判断C；根据全等三角形的判定定理可判断D.
2．【答案】C
【解析】【解答】解：∵DH⊥AB，
∴∠BHD=90°，
∴点O是BD的中点
∴BD=2OH=2×4=8，OD=OH=4；
∵ 菱形ABCD的面积为323，
∴S菱形ABCD=12AC·BD=323=12AC×8
解之：AC=83
∴OC=12AC=43
在Rt△COD中
CD=OC2+OD2=42+432=8.
故答案为：C.
【分析】利用垂直的定义可证得∠BHD=90°，利用直角三角形斜边上的中线等于斜边的一半，可求出BD，OD的长；再利用菱形的面积公式求出AC的长，即可得到OC的长；然后利用勾股定理求出CD的长.
3．【答案】D
【解析】【解答】解：A、∵将△ABC绕点C顺时针旋转60°得到△DEC，
∴∠BCE=∠ACD=60°，CB=CE，
∴△BCE是等边三角形，
∴BE=BC，故A正确；
B、∵点F是边AC中点，
∴CF=BF=AF=12AC，
∵∠BCA=30°，
∴BA=12AC，
∴BF=AB=AF=CF，
∴∠FCB=∠FBC=30°，
延长BF交CE于点H，则∠BHE=∠HBC+∠BCH=90°，

∴∠BHE=∠DEC=90°，
∴BF//ED，
∵AB=DE，
∴BF=DE，故B正确.
C、∵BF∥ED，BF=DE，
∴四边形BEDF是平行四边形，
∴BC=BE=DF，
∵AB=CF， BC=DF，AC=CD，
∴△ABC≌△CFD，
∴∠DFC=∠ABC=90°，故C正确；
D、.∵∠ACB=30°， ∠BCE=60°，
∴∠FCG=30°，
∴FG=12CG，
∴CG=2FG.
∵∠DCE=∠CDG=30°，
∴DG=CG，
∴DG=2FG.故D错误.
故答案为：D.
【分析】根据旋转的性质可得∠BCE=∠ACD=60°，CB=CE，推出△BCE是等边三角形，据此判断A；根据直角三角形斜边上中线的性质可得CF=BF=AF=12AC，根据含30°角的直角三角形的性质可得BA=12AC，则BF=AB=AF=CF，延长BF交CE于点H，则∠BHE=∠DEC=90°，推出BF//ED，结合AB=DE可判断B；易得四边形BEDF是平行四边形，则BC=BE=DF，证明△ABC≌△CFD，据此判断C；易得∠FCG=30°，则CG=2FG，根据∠DCE=∠CDG=30°可得DG=CG，进而判断D.
4．【答案】D
【解析】【解答】解：设B(m，a-1m)，
∵BD⊥y轴
∴S△BCD=12m⋅a-1m=5，
解得：a=11
故答案为：D.
【分析】设B（m，a-1m），则BD=m，△BCD的边BD上的高线为a-1m，接下来根据三角形的面积公式就可求出a的值.
5．【答案】B
【解析】【解答】解：∵CG∥AB，∠A=90°，
∴∠B=∠MCG，∠ACG=90°
∵点M为BC的中点，
∴BM=CM；
在△BMH和△CMG中
∠B=∠MCGBM=CM∠BMH=∠CMG
∴△BMH≌△CMG（ASA），
∴HM=MG，BH=CG；
∵四边形ACGH的周长为AH+AC+GH=AB+GH+AC=6+8+GH=14+GH；
∴当GH最小时，即GH⊥AB时，四边形ACGH的周长最小，
∴∠AHG=∠A=∠ACG=90°，
∴四边形ACGH是矩形，
∴AC=GH=8，
∴四边形ACGH的周长的最小值为14+8=22.
故答案为：B.
【分析】利用平行线的性质和垂直的定义可证得∠B=∠MCG，∠ACG=90° ，利用线段中点的定义可证得BM=CM；再利用ASA证明△BMH≌△CMG，利用全等三角形的性质可得到HM=MG，BH=CG；再利用垂线段最短可知即GH⊥AB时，四边形ACGH的周长最小值就是14+GH；然后证明四边形ACGH是矩形，利用矩形的性质可求出GH的长，即可求解.
6．【答案】B
【解析】【解答】解：设A（x，y），则OB=x，AB=y，
∵A为反比例函数y=1x图象上一点，
∴xy=1，
∴S△ABO=12AB•OB=12xy=12×1=12.
故答案为：B.
【分析】设A（x，y），则OB=x，AB=y，根据点A在反比例函数图象上可得xy=1，由三角形的面积公式可得S△ABO=12xy，据此计算.
7．【答案】D
【解析】【解答】∵AB∥CD ，∴∠ACD=∠BAC ，
∵AC 平分 ∠DAB ，∴∠BAC=∠CAD ，
∴∠ACD=∠CAD ，则 CD=AD=y ，即 △ACD 为等腰三角形，
过 D 点做 DE⊥AC 于点 E .

则 DE 垂直平分 AC ， AE=CE=12AC=3 ， ∠AED=90° ，
∵∠BAC=∠CAD ， ∠B=∠AED=90° ，
∴△ABC∽△AED ，
∴ACAD=ABAE ，∴6y=x3 ，
∴y=18x ，
∵在 △ABC 中， AB ∴x<6 ，
故 y 关于 x 的函数图象是D.
故答案为：D.
【分析】利用平行线的性质和角平分线的定义可证得∠ACD=∠CAD，利用等角对等边可证得CD=AD=y，过点D作DE⊥AC于点E，由等腰三角形的性质，可推出DE垂直平分AC，可求出AE的长；再证明是△ABC∽△AED，利用相似三角形的对应边成比例，可得到关于x，y的方程，然后将方程转化为函数解析式，可知此函数是反比例函数且x＜6，观察各选项中的图象，可得到符合题意的选项.
8．【答案】C
【解析】【解答】解：在Rt△CDE中，∠CDE=90°，∠DCE=40°，

则∠CED=90°-40°=50°，
∵l∥AB，
∴∠1=∠CED=50°.
故答案为：C.
【分析】根据直角三角形两锐角互余可得∠CED=90°-∠C=50°，根据平行线的性质可得∠1=∠CED，据此解答.
9．【答案】D
【解析】【解答】解：A、根据对顶角的概念可知，相等的角不一定是对顶角，故该选项不符合题意；
B、根据矩形的判定“对角线相等的平行四边形是矩形”可知该选项不符合题意；
C、根据三角形外心的定义，外心是三角形外接圆圆心，是三角形三条边中垂线的交点，故该选项不符合题意；
D、根据线段垂直平分线的性质可知该选项符合题意.
故答案为：D.
【分析】有公共顶点，且一个角的两边分别是另一个角的两边的反向延长线的两个角互为对顶角，据此可判断A；根据矩形的判定定理“对角线相等的平行四边形是矩形”可判断B；根据“外心是三角形外接圆圆心，是三角形三条边中垂线的交点”可判断C；根据线段垂直平分线的性质“ 线段垂直平分线上的点到线段两端的距离相等 ”可判断D.
10．【答案】A
【解析】【解答】解：令内切圆与BC交于点D，内切圆的圆心为O，连接AD，OB，
由题可知，圆中黑色部分的面积是圆面积的一半，

令BC=2a，则BD=a，
在等边三角形ABC中
AD⊥BC，OB平分∠ABC，
∴∠OBD=12∠ABC=30°，
由勾股定理，得AD=3a，
在Rt△BOD中，OD=tan30°×BD=33a，
∴圆中的黑色部分的面积与△ABC的面积之比为π(33a)2×1212×2a×3a=3π18.
故答案为：A.
【分析】令内切圆与BC交于点D，内切圆的圆心为O，连接AD，OB，由题可知：圆中黑色部分的面积是圆面积的一半，令BC=2a，则BD=a，根据等边三角形的性质可得AD⊥BC，∠OBD=30°，利用勾股定理可得AD，根据三角函数的概念可得OD，然后结合圆的面积公式进行计算.
11．【答案】110º
【解析】【解答】解：∵△ABC是等腰三角形，∠A=120º，
∴∠ABC=∠C=(180º-∠A)÷2=30º，
∵四边形ODEF是平行四边形，
∴OF∥DE，
∴∠2+∠ABE=180º，
即∠2+30º+40º=180º，
∴∠2=110º.
故答案为：110º.
【分析】根据等腰三角形的性质以及三角形的内角和定理可得∠ABC=∠C=30°，根据平行四边形的性质以及平行线的性质可得∠2+∠ABC+∠1=180º，据此计算.
12．【答案】48
【解析】【解答】解：在矩形ABCD中，BC=6cm，AC=10cm，

∴在Rt△ABC中，AB=102-62=8(cm)，
∴S矩形ABCD=AB×BC=8×6=48(cm2).
故答案为：48.
【分析】根据矩形的性质可得∠ABC=90°，利用勾股定理求出AB，然后根据矩形的面积公式进行计算.
13．【答案】①②③
【解析】【解答】解：∵AD绕点A沿顺时针方向旋转θ角度得到AD'
∴∠DAD'=θ，AD=AD'
∴∠CAB=∠DAD'
即∠CAD+∠DAB=∠DAB+∠BAD'
∴∠CAD=∠BAD'
∵∠CAD=∠BAD'AC=ABAD=AD'
得：△ADC≌△AD'B（SAS）
故①对
∵△ABC和△ADD'是顶角相等的等腰三角形
∴△ACB∼△ADD'
故②对
∴S△AD'DS△ABC=(ADAC)2
即AD最小时S△AD'D最小
当AD⊥BC时，AD最小
由等腰三角形三线合一，此时D点是BC中点
故③对
故答案为：①②③.
【分析】根据旋转的性质可得∠DAD′=θ，AD=AD′，由角的和差关系可得∠CAD=∠BAD′，然后根据全等三角形的判定定理可判断①；根据△ABC和△ADD′是顶角相等的等腰三角形结合相似三角形的判定定理可判断②；根据相似三角形的性质结合垂线段最短的性质可判断③.
14．【答案】12
【解析】【解答】解：如图所示：延长EF、DF分布交AC于点M、N，

∵FD∥BC，FE∥AB，BD=13BA，BE=14BC，
∴CE=3BE，AD=2BD，
∴CMAM=CEBE=3，ANCN=ADBD=2，
∴令AM=x，则CM=3x，
∴AC=4x，
∴AN=23AC=83x，CN=13AC=43x，
∴MN=53x，
∴NMAN=58，NMMC=59，
S△NMF：S△NAD=25：64，S△NMF：S△MEC=25：81，
∴设S△NMF=25a，S△NAD=64a，S△MEC=81a，
∴S四边形FECN=56a，
∴S△ABC=2+120a，
∴SADNS△ABC=64a2+120a=(ADAB)2=49，
求出a=112，
∴S△ABC=2+120a=12.
故答案为：12.
【分析】延长EF、DF分布交AC于点M、N，由已知条件得CE=3BE，AD=2BD，令AM=x，则CM=3x，AC=4x，AN=83x，CN=43x，MN=53x，则NMAN=58，NMMC=59，结合三角形面积公式得S△NMF∶S△NAD=25∶64，S△NMF∶S△MEC=25∶81，设S△NMF=25a，则S△NAD=64a，S△MEC=81a，S四边形FECN=56a，S△ABC=2+120a，结合S△ADNS△ABC=(ADAB)2就可求出a的值，进而可得S△ABC.
15．【答案】3
【解析】【解答】解：∵AB=AC，AD⊥BC，
∴CD=BD，
∵BC=6，
∴CD=3.
故答案为：3.
【分析】根据等腰三角形的三线合一可得BD=CD，然后结合BC的值就可求出CD的值.
16．【答案】40°
【解析】【解答】解：由反射定律得：∠FDO=∠CDB=20°，
∴∠DFO=180°-∠FDO-∠DOE=180°-20°-120°=40°，
∴∠AEF=∠DFO=40°.
故答案为：40°.

【分析】根据入射角等于反射角，可得∠CDB=∠EDO，∠DEO=∠AEF，根据三角形内角和定理求出∠OED的度数，从而求出结果.
17．【答案】（1）14π9
（2）2539
【解析】【解答】解：（1）∵∠AOD=2∠ABD=70°，
∴AD的长=70⋅π⋅4180=14π9；
故答案为：14π9；
（2）连接AD，

∵AC是切线，AB是直径，
∴AB⊥AC，
∴BC=AB2+AC2=82+62=10，
∵AB是直径，
∴∠ADB=90°，
∴AD⊥CB，
∴12⋅AB⋅AC=12⋅BC⋅AD，
∴AD=245，
∴BD=AB2-AD2=82-(245)2=325，
∵OB=OD，EO=ED，
∴∠EDO=∠EOD=∠OBD，
∴△DOE∽△DBO，
∴DODB=DEDO，
∴4325=DE4，
∴DE=52，
∴BE=BD-DE=325-52=3910，
∴DEBE=523910=2539.
故答案为：2539.
【分析】（1）根据圆周角定理可得∠AOD=2∠ABD=70°，然后结合弧长公式进行计算；
（2）连接AD，根据切线的性质可得AB⊥AC，由勾股定理可得AC，根据圆周角定理可得∠ADB=90°，然后根据△ABC的面积公式可求出AD，由勾股定理可得BD，根据等腰三角形的性质可得∠EDO=∠EOD=∠OBD，证明△DOE∽△DBO，根据相似三角形的性质可得DE，由BE=BD-DE可得BE，据此求解.
18．【答案】23
【解析】【解答】解：由作图可知MN垂直平分AB，
∴AD=BD，
∵△ACD的周长为AC+AD+CD=AC+BD+CD=AC+BC=8+15=23.
故答案为：23.
【分析】利用作图可知MN垂直平分AB，利用线段垂直平分线的性质可证得AD=BD，由此可得到△ACD的周长就是AC+BC，代入计算可求出△ACD的周长.
19．【答案】48
【解析】【解答】解：∵四边形ABCDE是正五边形，∠EAO是一个外角
∴∠EAO=360°5=72°
在△AEO中：
∠AEO=180°-∠EAO-∠MON=180°-72°-60°=48°
故答案为：48.
【分析】根据外角和定理可得∠EAO=360°5=72°，然后根据内角和定理进行计算.
20．【答案】（n-1+n，-n-1+n）
【解析】【解答】解：过B1作B1M1⊥x轴于M1，如图所示：

易知M1（1，0）是OA1的中点，
∴A1（2，0），
可得B1的坐标为（1，1），
∴B1O的解析式为：y＝x，
∵B1O∥A1B2，
∴A1B2的表达式一次项系数与B1O的一次项系数相等，
将A1（2，0）代入y＝x+b，
∴b＝﹣2，
∴A1B2的表达式是y＝x﹣2，
与y=1x（x＞0）联立，解得B2（1+2，﹣1+2），
仿上，A2（22，0），
B3（2+3，-2+3），
以此类推，点Bn的坐标为（n-1+n，-n-1+n）.
故答案为：（n-1+n，-n-1+n）.
【分析】过B1作B1M1⊥x轴于M1，根据等腰直角三角形的性质可得M1（1，0）是OA1的中点，则A1（2，0），B1（1，1），求出B1O、A1B2的解析式，联立反比例函数解析式求出x、y，可得B2（1+2，﹣1+2），同理可得A2、B3的坐标，进而推出Bn的坐标.
21．【答案】（1）证明：∵四边形ABCD是矩形，
∴AD//BC，
∴∠F＝∠BCE，
∵E是AB中点，
∴AE＝EB，
∵∠AEF＝∠BEC，
∴△AEF≌△BEC（AAS）．
（2）解：∵四边形ABCD是矩形，
∴∠D＝90°，
∵CD＝4，∠F＝30°，
∴CF＝2CD＝2×4＝8，
即CF的长为8．
【解析】【分析】（1）利用矩形的性质可知AD∥BC，利用平行线的性质可证得∠F=∠BCE，利用线段中点的定义可得到AE=BE；然后利用AAS可证得结论.
（2）利用矩形的性质可证得∠D=90°，利用30°角所对的直角边等于斜边的一半，可求出CF的长.
22．【答案】（1）证明：连接OE，

方法一：
∵AE平分∠BAC交BC于点E，
∴∠BAC＝2∠OAE，
∵∠FOE＝2∠OAE，
∴∠FOE＝∠BAC，
∴OE∥AB，
∵∠B＝90°，
∴OE⊥BC，
又∵OE是⊙O的半径，
∴BC是⊙O的切线；
方法二：
∵AE平分∠BAC交BC于点E，
∴∠OAE＝∠BAE，
∵OA＝OE，
∴∠OAE＝∠OEA，
∴∠BAE＝∠OEA，
∴OE∥AB，
∵∠B＝90°，
∴OE⊥BC，
又∵OE是⊙O的半径，
∴BC是⊙O的切线；
（2）解：连接EF，

∵CF＝2，sinC＝35，
∴OEOF+CF=35，
∵OE＝OF，
∴OE＝OF＝3，
∵OA＝OF＝3，
∴AC＝OA+OF+CF＝8，
∴AB＝AC•sinC＝8×35＝245，
∵∠OAE＝∠BAE，
∴cos∠OAE＝cos∠BAE，即ABAE=AEAF，∴245AE=AE3+3，
解得AE＝1255（舍去负数），
∴AE的长为1255．
【解析】【分析】（1）方法一：连接OE，利用角平分线的定义可证得∠BAC＝2∠OAE，利用圆周角定理可证得∠FOE＝2∠OAE，由此可推出∠FOE＝∠BAC，利用平行线的性质可证得OE⊥BC，然后利用切线的判定定理可证得结论；方法二：利用角平分线的定义可证得∠OAE＝∠BAE，利用等边对等角可知∠OAE＝∠OEA，由此可推出∠BAE＝∠OEA，利用平行线的判定定理可证得OE∥AB，再利用平行线的性质可证得OE⊥BC；然后根据切线的判定定理可证得结论.
（2）连接EF，利用解直角三角形可求出OF，OE的长，即可求出AC的长；再利用解直角三角形求出AB的长；由∠OAE=∠BAE，可得到cos∠OAE＝cos∠BAE，利用锐角三角函数的定义，可得到关于AE的方程，解方程求出AE的长.
23．【答案】（1）证明：连接OD，如图所示：

∵AD∥OC
∴∠ADO=∠DOC，∠DAO=∠BOC
∵OA=OD
∴∠ADO=∠DAO
∴∠DOC=∠BOC
∵OD=OB，OC=OC
∴△ODC≌△OBC
∴∠OBC=∠ODC
∵BC⊥AB
∴∠OBC=∠ODC=90°
∵OD为经过圆心的半径
∴CD是⊙O的切线.
（2）解：如图所示：作DM⊥BC交BC于点M

∵AB=8，AE=1，
∴OA=OB=OD=12AB=4，OE=OA-AE=3
DE=BM=OD2-OE2=7
令CM=x，CB=CD=x+7，BE=DM=7
∴在Rt△DMC，CM2+DM2=CD2
∴(x+7)2=72+x2，解得：x=37
∴BC=47
∵DE∥BC
∴△AEF∽△ABC
∴EFBC=AEAB=18=EF47
∴EF=72
【解析】【分析】（1）连接OD，根据平行线的性质可得∠ADO=∠DOC，∠DAO=∠BOC，根据等腰三角形的性质可得∠ADO=∠DAO，则∠DOC=∠BOC，利用SAS证明△ODC≌△OBC，得到∠OBC=∠ODC=90°，据此证明；
（2）作DM⊥BC交BC于点M，由题意可得OA=OB=OD=4，OE=OA-AE=3，利用勾股定理可得DE，令CM=x，则CB=CD=7x，根据勾股定理可得x，据此可得BC，易证△AEF∽△ABC，然后根据相似三角形的性质进行计算.
24．【答案】（1）解：把点A(-1，2)代入y=kx(k≠0)得：2=k-1，
∴k=-2，
∴反比例函数的解析式为y=-2x
（2）解：∵反比例函数y=kx(k≠0)与正比例函数y=mx(m≠0)的图象交于点A(-1，2)和点B，
∴B(1，-2)，
∵点C是点A关于y轴的对称点，
∴C(1，2)，
∴AC=2，
∴S△ABC=12×2×(2+2)=4
（3）解：根据图象得：不等式kx 【解析】【分析】（1）将A（-1，2）代入y=kx中求出k的值，据此可得反比例函数的解析式；
（2）易得B（1，-2），根据点C是点A关于y轴的对称点可得C（1，2），则CA=2，然后根据三角形的面积公式进行计算；
（3）根据图象，找出反比例函数图象在正比例函数图象下方部分所对应的x的范围即可.
25．【答案】（1）解：∠BAC=90°，AB= AC，
∴∠ABC=∠ACB=90°2=45°，
∵l∥BC，
∴∠DAB=∠ABC=45°，∠EAC=∠ACE=45° ，
∴BD⊥AE，CE⊥DE，
即∠BDA=∠CEA=90° ，
∴∠ABD=90°-45° =45°，∠ACE = 90°-45° =45° ，
∴∠DAB=∠ABD=∠EAC=∠ACE=45° ，
∴AD=BD=ABsin∠DAB =2×22=1，
∴AE=CE= ACsin∠EAC=2×22=1，
∴DE=AD+AE=2；
（2）解：（Ⅰ） DE=CE+BD；理由如下：
∵BD⊥AE， CE⊥DE，
∴∠BDA=∠CEA=90° ，
∴∠DAB+∠DBA=90° ，
∴∠BAC=90° ，
∴∠DAB+∠CAE=90° ，
∴∠DBA=∠CAE，
∴AB=AC，
∴△ABD≌△CAE，
∴AD=CE，BD=AE，
∴DE=AD+AE=CE+BD，
即DE=CE+BD；
（Ⅱ） BD=CE+DE，理由如下：
∵BD⊥AE，CE⊥DE，
∴∠BDA=∠CEA=90° ，
∴∠DAB+∠DBA=90° ，
∵∠BAC= 90°，
∴∠DAB+∠CAE=90° ，
∴∠DBA=∠CAE，
∵AB=AC，
∴△ABD≌△CAE（AAS），
∴AD=CE，BD=AE，
∴BD=AE=AD+DE=CE+DE，
即BD=CE+DE.
（3）解：由(2) 可知，AD=CE=3，
∴AE= AD+DE=3+1=4，
在Rt△AEC中，
AC=AE2+CE2=5，
∵BD⊥AE，CE⊥AE，
∴DF∥CE，
∴ADAE=AFCF，
即34=AF5，
解得：AF=154，
∴CF=AC-AF=5-154=54，
∵AB=AC=5，
∴S△BFC=12CF×AB=12×54×5=258.
【解析】【分析】(1)根据平行线的性质和等腰直角三角形的性质求出求出∠ABD=45°，∠ACE=45°，然后根据锐角三角函数定义求出AD=BD=1，AE=CE=1，即可求出DE= AD+ AE=2；
(2) (Ⅰ) DE=CE+BD；利用AAS证明△ABD≌△CAE，得出AD=CE，BD=AE，利用线段和差即可得出结论；
(Ⅱ) BD=CE+DE；同理，利用AAS证明△ABD≌△CAE，得出AD=CE，BD=AE，利用线段和差即可得出结论；
(3)先求出AE长，在Rt△AEC中，根据勾股定理求出AC的长，由DF∥CE，根据平行线分线段成比例的性质列式求出AF长，则可求出CF，最后计算△BFC的的面积即可.
26．【答案】（1）证明：连接AD、OD，记 ∠ABD=∠1 ， ∠ODB=∠2 ，

∵DE⊥AC ，
∴∠CED=90° .
∵AB=AC ，
∴∠1=∠C .
∵OB=OD ，
∴∠1=∠2 ，
∴∠C=∠2 ，
∴OD∥AC ，
∴∠ODE=∠CED=90° ，
∴PE⊥OD ，
又∵OD是⊙O的半径，
∴直线PE是⊙O的切线.
（2）解：连接AD，

∵AB是直径，
∴∠ADB=90° ，
∴AD⊥BC .
又∵AB=AC ，
∴CD=12BC ，
∵∠P=30° ， ∠PEA=90° ，
∴∠PAE=60° ，
又∵AB=AC ，
∴△ABC 为等边三角形，
∴∠C=60° ， BC=AB=12 ，
∴CD=12BC=6 ，
在 Rt△CDE 中，∵cosC=CECD ，
∴CE=CDcos60°=6×12=3
【解析】【分析】（1）连AD、OD，记∠ABD=∠1，∠ODB=∠2，由等腰三角形性质得∠1=∠C，∠1=∠2，则∠C=∠2，推出OD∥AC，由平行线的性质可得∠ODE=∠CED=90°，据此证明；
（2）连接AD，由圆周角定理可得∠ADB=90°，结合等腰三角形的性质得CD=12BC，易得△ABC 为等边三角形，得到∠C=60°，BC=AB=12，CD=12BC=6，然后根据三角函数的概念就可求出CE.
27．【答案】（1）解：AC与⊙O的位置关系为相切，理由如下，
连接OD，如图所示

∵BD为∠ABC的角平分线
∴∠ABD=∠CBD
又∵⊙O过点B、D，设⊙O半径为r
∴OB=OD=r
∴∠ODB=∠OBD=∠CBD
∴OD//BC（内错角相等，两直线平行）
∵OD⊥AC
∴AC与⊙O的位置关系为相切.
（2）解：①∵BC=3，CD=32
∴BD=BC2+CD2=352
∴sin∠DBC=CDBD=55
过点D作DF⊥AB交于一点F，如图所示

∴CD=DF（角平分线的性质定理）
∴BF=BC=3
∴OF=BF-OB=3-r，OF=CD=32
∴OD2=OF2+DF2即r2=(3-r)2+(32)2
∴r=158
∵OD//BC
∴∠ABC=∠FOD
∴sin∠ABC=sin∠FOD=DFOD=45
∴sin∠DBC=55，sin∠ABC=45；
②cos∠DBC=CBBD=255
∴sin∠DBC×cos∠DBC=55×255=25
∴sin∠ABC=2sin∠DBC×cos∠DBC
猜测sin2α=2sinαcosα
当α=30°时2α=60°
∴sin2α=sin60°=32
sinα=sin30°=12
cosα=cos30°=32
∴sin2α=2sinαcosα=2×12×32=32=sin2α
∴sin2α=2sinαcosα.
【解析】【分析】（1）连接OD，根据角平分线概念得∠ABD=∠CBD，设OB=OD=r，结合等腰三角形性质得∠ODB=∠OBD=∠CBD，推出OD∥BC，结合BC⊥AD可得OD⊥AC，据此证明；
（2）①利用勾股定理可得BD，根据三角函数的概念可得sin∠DBC的值，过点D作DF⊥AB交于一点F，根据角平分线的性质可得CD=DF，则BF=BC=3，OF=3-r，OF=CD=32，利用勾股定理可得r，根据平行线的性质可得∠ABC=∠FOD，然后结合三角函数的概念进行解答；②根据三角函数的概念求出cos∠DBC、sin∠DBC、cos∠DBC的值，猜想sin2α=2sinαcosα，令α=30°，求出sin2α、sinα、cosα的值，据此证明.