




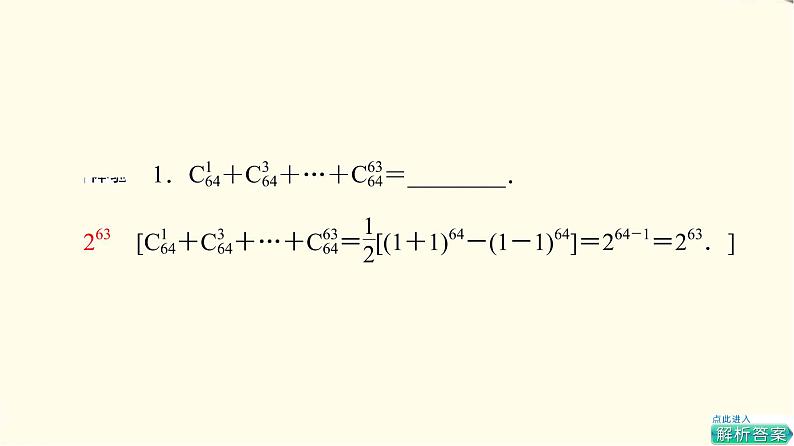








高中数学苏教版 (2019)选择性必修第二册7.4二项式定理多媒体教学ppt课件
展开7.4.2 二项式系数的性质及应用
学 习 目 标 | 核 心 素 养 |
1.理解和掌握二项式系数的性质,并会简单应用.(难点) 2.理解和初步掌握赋值法及其应用.(重点) | 1.通过学习二项式系数的性质,培养逻辑推理的素养. 2.借助二项式系数的性质解题,提升数学运算的素养. |
用计算工具计算(a+b)n的展开式的二项式系数,然后观察系数,有没有明显的规律?上下两行有什么关系?你能发现其他规律吗?
知识点 二项式系数的性质
(a+b)n展开式的二项式系数C,C,…,C有如下性质:
(1)C=C;
(2)C+C=C;
(3)当r<时,C<C;当r>时,C<C;
(4)C+C+…+C=2n.
1.C+C+…+C=________.
263 [C+C+…+C=[(1+1)64-(1-1)64]=264-1=263.]
2.C+C=________.(用组合数表示)
C [C+C=C.]
3.(2-x)10的展开式中的各项系数和为________.
1 [令x=1即得各项系数和,∴各项系数和为1.]
类型1 求展开式的系数和
【例1】 设(1-2x)2 022=a0+a1x+a2x2+…+a2 022·x2 022(x∈R).
(1)求a0+a1+a2+…+a2 022的值;
(2)求a1+a3+a5+…+a2 021的值;
(3)求|a0|+|a1|+|a2|+…+|a2 022|的值.
[解] (1)令x=1,得
a0+a1+a2+…+a2 022=(-1)2 022=1. ①
(2)令x=-1,得
a0-a1+a2-…-a2 021+a2 022=32 022. ②
①-②得
2(a1+a3+…+a2 021)=1-32 022,
∴a1+a3+a5+…+a2 021=.
(3)∵Tr+1=C(-2x)r=(-1)r·C·(2x)r,
∴a2k-1<0(k∈N*),a2k>0(k∈N).
∴|a0|+|a1|+|a2|+|a3|+…+|a2 022|=a0-a1+a2-a3+…-a2 021+a2 022=32 022.
在本例条件不变的情况下,求下列各式的值.
(1)a2+a4+a6+…+a2 022;
(2)a1+2a2+3a3+…+2 022a2 022.
[解] (1)由,
得2(a0+a2+…+a2 022)=32 022+1,
∴a0+a2+…+a2 022=,
又令x=0得a0=1,∴a2+a4+a6+…+a2 022=.
(2)∵(1-2x)2 022=a0+a1x+a2x2+…+a2 022x2 022(x∈R),
∴两边分别求导得
-4 044(1-2x)2 021=a1+2a2x+…+2 022a2 022x2 021(x∈R),
令x=1得,4 044=a1+2a2+…+2 022a2 022.
即a1+2a2+3a3+…+2 022a2 022=4 044.
二项展开式中系数和的求法
(1)对形如(ax+b)n,(ax2+bx+c)m(a,b,c∈R,m,n∈N*)的式子求其展开式的各项系数之和,常用赋值法,只需令x=1即可;对(ax+by)n(a,b∈R,n∈N*)的式子求其展开式各项系数之和,只需令x=y=1即可.
(2)一般地,若f(x)=a0+a1x+a2x2+…+anxn,则f(x)展开式中各项系数之和为f(1),
奇数项系数之和为a0+a2+a4+…=,
偶数项系数之和为a1+a3+a5+…=.
1.已知(2x-3)4=a0+a1x+a2x2+a3x3+a4x4,求:
(1)a0+a1+a2+a3+a4;
(2)(a0+a2+a4)2-(a1+a3)2.
[解] (1)由(2x-3)4=a0+a1x+a2x2+a3x3+a4x4,
令x=1得(2-3)4=a0+a1+a2+a3+a4,
所以a0+a1+a2+a3+a4=1.
(2)在(2x-3)4=a0+a1x+a2x2+a3x3+a4x4中,
令x=1得(2-3)4=a0+a1+a2+a3+a4, ①
令x=-1得(-2-3)4=a0-a1+a2-a3+a4. ②
所以(a0+a2+a4)2-(a1+a3)2
=(a0-a1+a2-a3+a4)(a0+a1+a2+a3+a4)
=(-2-3)4(2-3)4=(2+3)4(2-3)4=625.
类型2 二项式系数性质的应用
[探究问题]
1.计算,并说明二项式系数的单调性.
[提示] =.
当k<时,>1,二项式系数逐渐增大;
同理,当k>时,二项式系数逐渐减小.
2.如何求(a+bx)n(a,b∈R)的展开式中系数最大的项?
[提示] 求(a+bx)n(a,b∈R)的展开式系数最大的项,一般是采用待定系数法,设展开式各项系数分别为A1,A2,…,An+1,且第r+1项系数最大,应用解出r,即得系数的最大项.
【例2】 已知f(x)=(+3x2)n展开式中各项的系数和比各项的二项式系数和大992.
(1)求展开式中二项式系数最大的项;
(2)求展开式中系数最大的项.
求二项式系数最大的项,利用性质知展开式中中间项或中间两项是二项式系数最大的项;求展开式中系数最大的项,必须将x,y的系数均考虑进去,包括“+”“-”号.
[解] 令x=1,则二项式各项系数的和为f(1)=(1+3)n=4n,又展开式中各项的二项式系数之和为2n.由题意知,4n-2n=992.
∴(2n)2-2n-992=0,
∴(2n+31)(2n-32)=0,
∴2n=-31(舍去)或2n=32,
∴n=5.
(1)由于n=5为奇数,∴展开式中二项式系数最大的项为中间两项,它们分别是
T3=C(x)3(3x2)2=90x6,
T4=C(x)2(3x2)3=270x.
(2)展开式的通项公式为Tr+1=C3r·x (5+2r).
假设Tr+1项系数最大,
则有
∴
∴
∴≤r≤,
∵r∈N*,
∴r=4.
∴展开式中系数最大的项为T5=Cx (3x2)4=405x.
1.求二项式系数最大的项,根据二项式系数的性质,当n为奇数时,中间两项的二项式系数最大;当n为偶数时,中间一项的二项式系数最大.
2.求展开式中系数最大项与求二项式系数最大项是不同的,需根据各项系数的正、负变化情况进行判断,一般采用列不等式组,解不等式的方法求得.
2.已知的展开式.
(1)求二项式系数最大的项;
(2)系数的绝对值最大的项是第几项.
[解] 通项为Tr+1=C·()8-r·=(-1)r·C·2r·x.
(1)二项式系数最大的项为中间项,即为第5项.
故T5=C·24·x=1 120·x-6.
(2)设第r+1项系数的绝对值最大,
则
即整理得
所以r=5或r=6,故系数绝对值最大的项为第6项和第7项.
类型3 二项式系数性质的应用
【例3】 求证:32n+2-8n-9能被64整除(n∈N*).
[证明] 当n=1时,验证成立;
当n≥2时,32n+2-8n-9=9(8+1)n-8n-9
=9(8n+C·8n-1+…+C·82+C·8+C)-8n-9
=9(8n+C·8n-1+…+C·82)+64n.
因为各项均能被64整除,所以32n+2-8n-9能被64整除.
对含指数式的整除问题,常用二项式定理证明,通常将被除数的底数化为除数或除数的倍数与一个数的和或差的形式,利用二项式定理展开,化简的各项都是除数的倍数,故展开后的多项式能被除数整除,从而证明了原式能被除数整除.
3.(1)求证:2n+2·3n+5n-4能被25整除(n∈N*);
(2)求证:1+3+32+…+33n-1能被26整除(n为大于1的偶数).
[证明] (1)原式=4(5+1)n+5n-4
=4(C·5n+C·5n-1+C·5n-2+…+C)+5n-4
=4(C·5n+C·5n-1+…+C·52)+25n,
以上各项均为25的整数倍,故得证.
(2)1+3+32+…+33n-1==(33n-1)
=(27n-1)=[(26+1)n-1],
而(26+1)n-1=C·26n+C·26n-1+…+C·26,
因为n为大于1的偶数,
所以[(26+1)n-1]能被26整除,
所以1+3+32+…+33n-1能被26整除.
1.(多选题)二项式的展开式中,系数最大的项为( )
A.第五项 B.第六项
C.第七项 D.第八项
BC [二项式的展开式中,每项的系数与二项式系数相等,共有12项,所以系数最大的项为第六项和第七项.]
2.(1+y)n的展开式中,所有的二项式系数之和等于512,则第3项是( )
A.Cy3 B.Cy2 C.Cy3 D.Cy2
B [由题可得2n=512,故n=9,故T3=Cy2.]
3.C+C+C+C+C的值为________.
62 [原式=26-C-C=62.]
4.二项式(a+b)n+1的展开式中,奇数项的二项式系数之和为________.
2n [由于(a+b)n的展开式的奇数项的二项式系数之和为2n-1,所以(a+b)n+1的展开式的奇数项的二项式系数之和为2n+1-1=2n.]
5.设(x2+1)(2x+1)9=a0+a1(x+2)+a2(x+2)2+…+a11(x+2)11,则a0+a1+a2+…+a11的值为________.
-2 [令x=-1,则原式化为[(-1)2+1][2×(-1)+1]9=-2
=a0+a1(2-1)+a2(2-1)2+…+a11(2-1)11,
∴a0+a1+a2+…+a11=-2.]
回顾本节知识,自我完成以下问题:
1.如何求二项展开式的系数和?
[提示] 二项式系数的和是公式性的,要牢记,而系数和的求法是用“赋值法”,针对不同的问题,赋值不同,通常令未知数为1或-1等.
2.如何求二项式系数的最大值?
[提示] 求二项式系数的最大项,根据二项式系数的性质对(a+b)n中的n进行讨论.
(1)当n为奇数时,中间两项的二项式系数最大.
(2)当n为偶数时,中间一项的二项式系数最大.
高中数学人教B版 (2019)选择性必修 第二册3.3 二项式定理与杨辉三角示范课课件ppt: 这是一份高中数学人教B版 (2019)选择性必修 第二册3.3 二项式定理与杨辉三角示范课课件ppt,文件包含人教B版高中数学选择性必修第二册33《二项式系数的性质杨辉三角和二项式定理的应用》第2课时课件ppt、人教B版高中数学选择性必修第二册33《二项式系数的性质杨辉三角和二项式定理的应用》第2课时教案doc等2份课件配套教学资源,其中PPT共51页, 欢迎下载使用。
高中苏教版 (2019)7.4二项式定理精品ppt课件: 这是一份高中苏教版 (2019)7.4二项式定理精品ppt课件,共20页。PPT课件主要包含了二项式系数的性质,杨辉三角,赋值法的应用,随堂小测等内容,欢迎下载使用。
苏教版 (2019)选择性必修第二册7.4二项式定理试讲课ppt课件: 这是一份苏教版 (2019)选择性必修第二册7.4二项式定理试讲课ppt课件,共22页。PPT课件主要包含了学习目标,活动方案,检测反馈等内容,欢迎下载使用。













