2022-2023学年重庆市涪陵十四中八年级（上）期中数学试卷（含解析）

2022-2023学年重庆市涪陵十四中八年级（上）期中数学试卷

副标题

一、选择题（本大题共12小题，共48.0分。在每小题列出的选项中，选出符合题目的一项）

1.    的倒数是(    )

A.  B.  C.  D.

2.    下列图形中是轴对称图形的是(    )

A. 赵爽弦图 B. 科克曲线
C. 斐波那契螺旋线 D. 费马螺线

3.    若长度分别为，，的三条线段能组成一个三角形，则的值可以是(    )

A.  B.  C.  D.

4.    在平面直角坐标系中，点关于轴的对称点的坐标是(    )

A.  B.  C.  D.

5.    如图，，，，则的度数是(    )

A.
B.
C.
D.

6.    下列命题错误的是(    )

A. 三角形的三条高交于一点
B. 三角形的三条中线都在三角形内部
C. 直角三角形的三条高交于一点，且交点在直角顶点处
D. 三角形的三条角平分线交于一点，且这个交点到三角形三边的距离相等

7.    估算的值在(    )

A. 到之间 B. 到之间 C. 到之间 D. 到之间

8.    如图，有一池塘，要测池塘两端，的距离，可先在平地上取一个点，从点不经过池塘可以直接到达点和连接并延长到点，使，连接并延长到点，使连接，那么量出的长就是，的距离．这里构造了全等三角形，≌，那么判断这两个三角形全等的依据是(    )

A.  B.  C.  D.

9.    如图，中，，平分，交于点，，，则的长为(    )

A.
B.
C.
D.

10. 如图，是中边上的垂直平分线，如果，，则的周长为(    )

A.
B.
C.
D.

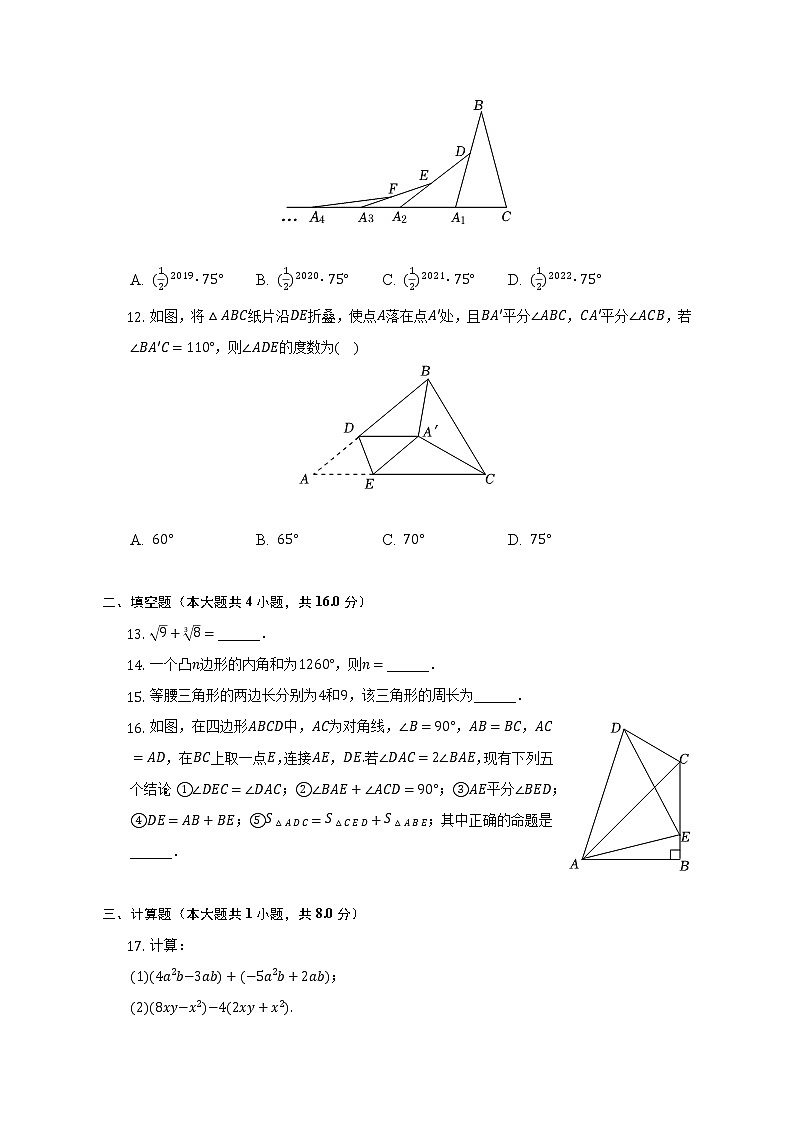
11. 如图，在第个中，，，在边上任取一点，延长到，使，得到第个；在边上任取一点，延长到，使，得到第个；按此做法继续下去，则第个三角形中以为顶点的内角度数是(    )

A.  B.  C.  D.

12. 如图，将纸片沿折叠，使点落在点处，且平分，平分，若，则的度数为(    )

A.  B.  C.  D.

二、填空题（本大题共4小题，共16.0分）

13. ______．
14. 一个凸边形的内角和为，则______．
15. 等腰三角形的两边长分别为和，该三角形的周长为______．
16. 如图，在四边形中，为对角线，，，，在上取一点，连接，若，现有下列五个结论：；；平分；；；其中正确的命题是______．

三、计算题（本大题共1小题，共8.0分）

17. 计算：
    ；
     

四、解答题（本大题共8小题，共78.0分。解答应写出文字说明，证明过程或演算步骤）

18. 本小题分
    解下列不等式：
    ；
    ．
19. 本小题分
    如图，点，，，在同一条直线上，，，求证：．

20. 本小题分
    如图，在中，，，是边上的高．
    尺规作图：作的角平分线交于点保留作图痕迹，不写作法，不写结论；
    在的条件下，求的度数．

21. 本小题分
    如图，在平面直角坐标系中，其中点，，的坐标分别为，，．
    作关于轴对称的，其中点，，的对应点分别为点，，，并写出点，，的坐标；
    计算的面积．

22. 本小题分
    如图，在中，，，为延长线上一点，点在边上，且，连结、、．
    求证：≌；
    若，求的度数．

23. 本小题分
    如图，在中，，是边上的中线，延长至点，使，连接求证：．

24. 本小题分
    学习自然数时，我们发现一种特殊的自然数“积数”
    定义：对于三位自然数，各位数字都不为，且百位数字与个位数字之积恰好能被十位数字整除，则称这个自然数为“积数”，例如：是“积数”，因为，，都不为，且，能被整除；不是“积数”，因为，不能被整除．
    判断，是否是“积数”？并说明理由；
    求出百位数字比个位数字大的所有“积数”，并说明理由．
25. 本小题分
    如图，等腰中，，点、分别在坐标轴上．
    如图，若点的横坐标为，求点的坐标；
    如图，若轴恰好平分，交轴于点，过点作轴于点，求的值；
    如图，若点的坐标为，点在轴的正半轴上运动时，分别以、为边在第一、第二象限作等腰，等腰，连接交轴于点，当点在轴上移动时，的长度是否发生改变？若不变，求出的值，若变化，求的取值范围．
    
    

答案和解析

1.【答案】 

【解析】解：，
的倒数是．
故选：．
根据倒数的定义：若两个数的乘积是，我们就称这两个数互为倒数．
本题主要考查倒数的定义，要求熟练掌握．需要注意的是：
倒数的性质：负数的倒数还是负数，正数的倒数是正数，没有倒数．
倒数的定义：若两个数的乘积是，我们就称这两个数互为倒数．
 

2.【答案】 

【解析】解：，，选项中的图形都不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
选项中的图形能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；
故选：．
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
 

3.【答案】 

【解析】解：由三角形三边关系定理得：，
即，
即符合的只有，
故选：．
根据三角形三边关系定理得出，求出即可．
本题考查了三角形三边关系定理，能根据定理得出是解此题的关键，注意：三角形的两边之和大于第三边，三角形的两边之差小于第三边．
 

4.【答案】 

【解析】解：点关于轴的对称点的坐标是．
故选：．
根据平面直角坐标系中任意一点，关于轴的对称点的坐标是即可得出答案．
本题主要考查了平面直角坐标系中对称点的规律．解决本题的关键是掌握好对称点的坐标规律：
关于轴对称的点，横坐标相同，纵坐标互为相反数；
关于轴对称的点，纵坐标相同，横坐标互为相反数；
关于原点对称的点，横坐标与纵坐标都互为相反数．
 

5.【答案】 

【解析】解：，
，
，，
．
故选：．
利用平行的性质求出，再利用三角形外角的性质求出即可．
本题考查的是平行线的性质及三角形内角与外角的关系：两直线平行，内错角相等；三角形的一个外角等于和它不相邻的两个内角的和．
 

6.【答案】 

【解析】解：、钝角三角形的三条高线段不能交于一点，是三条高所在的直线交于一点，故原命题错误，符合题意；
B、三角形的三条中线都在三角形的内部，正确，不符合题意；
C、直角三角形的三条高交于一点，且交点在直角顶点处，正确，不符合题意；
D、三角形的三条角平分线交于一点，且这个交点到三角形三边的距离相等，正确，不符合题意．
故选：．
利用三角形的垂心的定义、重心的定义及三角形的角平分线的性质分别判断后即可确定正确的选项．
本题考查了命题与定理的知识，解题的关键是了解三角形的垂心的定义、重心的定义及三角形的角平分线的性质，难度不大．
 

7.【答案】 

【解析】解：，，而，
，
，
故选：．
根据算术平方根的定义，估算无理数的大小，进而得出的大小即可．
本题考查估算无理数的大小，掌握算术平方根的定义是正确解答的前提．
 

8.【答案】 

【解析】解：量出的长就等于的长，理由如下：
在和中，
，
≌，
，
故选：．
利用“边角边”证明和全等．
本题考查了全等三角形的应用，熟练掌握三角形全等的判定方法是解题的关键．
 

9.【答案】 

【解析】解：如图，过点作于，
，平分，
，
，
解得：，
．
故选：．
过点作于，根据角平分线上的点到角的两边距离相等可得，然后利用的面积列式计算即可得解．
本题考查了三角形的面积和角平分线的性质，能熟记角平分线上的点到角两边的距离相等是解此题的关键．
 

10.【答案】 

【解析】解：是边上的垂直平分线，
，
，，
的周长


，
故选：．
根据线段垂直平分线的性质，可得，从而可得的周长，进行计算即可解答．
本题考查了线段垂直平分线的性质，熟练掌握线段垂直平分线的性质是解题的关键．
 

11.【答案】 

【解析】解：，，
，．
．
．
，
．
．
．
同理可得：．
，
以此类推，以为顶点的内角度数是．
以为顶点的内角度数是．
故选：．
根据等腰三角形的性质，由，，得，，那么由，得根据三角形外角的性质，由，得以此类推，运用特殊到一般的思想解决此题．
本题主要考查等腰三角形的性质、三角形内角和定理、三角形外角的性质，熟练掌握三角形外角的性质以及特殊到一般的猜想归纳思想是解决本题的关键．
 

12.【答案】 

【解析】解：如图，连接，
平分，平分，，
，
，
，
，，
，，
，
平分，平分，
平分，
，
，
．
故选：．
连接，根据三角形内角和求出，再根据，，得出，从而得出答案．
本题考查三角形的内角和定理、角平分线的定义、三角形的外角的性质等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识．
 

13.【答案】 

【解析】解：．
故答案为：．
直接利用算术平方根以及立方根的性质化简得出答案．
此题主要考查了实数运算，正确化简各数是解题关键．
 

14.【答案】 

【解析】解：由题意得，，
解得，，
故答案为：．
根据多边形内角和定理列式计算即可．
本题考查的是多边形的内角与外角，掌握多边形内角和定理：且为整数是解题的关键．
 

15.【答案】 

【解析】解：分两种情况：
当为底边长，为腰长时，，
三角形的周长；
当为底边长，为腰长时，
，
不能构成三角形；
这个三角形的周长是．
故答案为：．
分类讨论：为腰长，为底边长，根据三角形的周长公式，可得答案．
本题考查了等腰三角形的性质、三角形的三边关系；熟练掌握等腰三角形的性质，通过进行分类讨论得出结果是解决问题的关键．
 

16.【答案】 

【解析】解：设，则，
，，
，
，
，
，
，
，
，
点、、、共圆，
，
故正确；
由得：，
，
，
故正确；
由得：点、、、共圆，
，，
，
，
故正确；
如图，

作于，
由得：平分，
，
，
点、、、共圆，
，
，
，
，
，，
，
，
，
故正确；
如上图，
，，，
≌，
，
，
，
，
，
故不正确，
故答案为：．
设，依次表示出，，，，从而计算得，从而得出点、、、共圆，进一步得出结果；
计算可得出结果；
可推出，，进一步得出结果；
作，可推出，，进一步得出结果；
可推出的面积大于的面积，进而得出的面积大于与的面积之和，进一步得出的面积大于与的面积之和．
本题考查了等腰三角形的性质，全等三角形判定和性质，确定圆的条件等知识，解决问题的关键寻找角之间数量关系．
 

17.【答案】解：

；


． 

【解析】先去括号，然后合并同类项；
先去括号，然后合并同类项．
本题考查了整式的加减，整式的加减的实质就是去括号、合并同类项．一般步骤是：先去括号，然后合并同类项．
 

18.【答案】解：，
，
，
，
；
，
，
，
，
，
． 

【解析】按照解一元一次不等式的步骤：去括号，移项，合并同类项，系数化为，进行计算即可解答；
按照解一元一次不等式的步骤：去分母，去括号，移项，合并同类项，系数化为，进行计算即可解答．
本题考查了解一元一次不等式，熟练掌握解一元一次不等式的步骤是解题的关键．
 

19.【答案】解：，
．
即．
在和中，
，
≌，
． 

【解析】证≌，即可得出结论．
本题考查了全等三角形的判定与性质，证明≌是解题的关键．
 

20.【答案】解：如图，射线即为所求；

，，
，
平分，
，
，
，
． 

【解析】利用尺规作出的角平分线即可；
分别求出，，可得结论．
本题考查作图基本作图，等腰三角形的性质，三角形内角和定理等知识，解题的关键是掌握五种基本作图，属于中考常考题型．
 

21.【答案】解：如图，的即为所求．，，，；

的面积． 

【解析】利用轴对称变换的性质分别作出，，的对应点，，即可；
把三角形的面积看成矩形的面积减去周围的三个三角形面积即可．
本题考查作图轴对称变换，三角形的面积等知识，解题的关键是掌握轴对称变换的性质，属于中考常考题型．
 

22.【答案】证明：在和中，
，
≌；

解：在中，，，
，
由得：≌，
，
为的外角，
，
则． 

【解析】此题考查了全等三角形的判定与性质，以及三角形的外角性质，熟练掌握全等三角形的判定与性质是解本题的关键．
利用即可得证；
由全等三角形对应角相等得到，利用外角的性质求出的度数，即可确定出的度数．
 

23.【答案】证明：取的中点，连接，
，点，分别是，的中点，
，
在和中，
，
≌，
，
，，
，
，
是的中位线，
，
． 

【解析】取的中点，连接，由判定≌，得到，再利用三角形中位线定理得到，即可得出结论．
本题考查的是三角形中位线定理、全等三角形的判定和性质、等腰三角形的性质以及三角形中位线定理等知识，正确作出辅助线、构造三角形全等是解题的关键．
 

24.【答案】解：，因为，不能被整除，
不是“积数”，
，因，，，都不为，且，能被整除，
是“积数”；
设个位数字为，十位数字为，则百位数字为，且，
由题意得：能被整除，
当时，的值为，，
此时该数是，，，
当时，的值为，，，，
此时该数是：，，，，
当时，的值为，，，，
此时该数是：，，，
百位数字比个位数字大的所有“积数”为：，，，，，，，，． 

【解析】根据题意中的新定义求解；
设个位数字为，十位数字为，则百位数字为，且，根据整除的意义验证求解．
本题考查了因式分解的应用，整除的意义是解题的关键．
 

25.【答案】解：如图，作于，
，，
，
在和中，
，
≌，
，
点坐标；

设，
则，
即轴平分，
，
即，
，
，
解得，
则，

且
∽，
，
即，
；
解法二：延长交的延长线于点．

可证≌，
，
再证明，可得，
．

如图，作轴于，
，，
，
在和中，
，
≌，
，，
，
，
在和中，
，
≌，
，
． 

【解析】作，易证≌，根据全等三角形对应边相等的性质即可解题；
设，根据勾股定理求出，根据即轴平分，得到，求得，，，再证明∽，得到，即，即可解答，
作轴，易证≌和≌，可得和，即可求得，即可解题．
本题考查了勾股定理、角平分线的性质、相似三角形的判定与性质，熟练掌握三角形全等的证明是解本题的关键．