

四川省绵阳市涪城区2022-2023学年八年级上学期期中数学试卷(含答案)
展开2022-2023学年四川省绵阳市涪城区八年级(上)期中数学试卷
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
- 下列标志是轴对称图形的是( )
A. B.
C. D.
- 下列说法正确的是( )
A. 全等三角形是指面积相等的两个三角形
B. 全等三角形是指形状相同的两个三角形
C. 两个周长相等的三角形是全等三角形
D. 全等三角形的周长、面积分别相等
- 李老师给班级中的小雨同学三根木条,小雨同学用三根木条拼成了三角形,已知其中两根木条的长度分别为、,则第三根木条的长度可能是( )
A. B. C. D.
- 在中,,,,直线是中边的垂直平分线,是直线上的一动点,则的周长的最小值为( )
A. B. C. D.
- 下列关于三角形外角的描述正确的是( )
A. 三角形的外角大于三角形的任意一个内角
B. 三角形的外角中最多有两个锐角
C. 钝角三角形外角和大于
D. 若三角形有一个外角为锐角,则这个三角形一定是钝角三角形
- 在下列条件中不能判定为直角三角形的是( )
A. B.
C. D.
- 将一个四边形截去一个角后,所形成的一个新的多边形的内角和是( )
A. B.
C. 或 D. 或或
- 已知点和点关于轴对称,则的值为( )
A. B. C. D.
- 已知≌,若,,,则的长为( )
A. B. C. D.
- 如图,,,据此可以证明≌,依据是( )
A.
B.
C.
D.
- 如图,是中的平分线,,交于点,,交于点,若,,则的面积是( )
A. B. C. D.
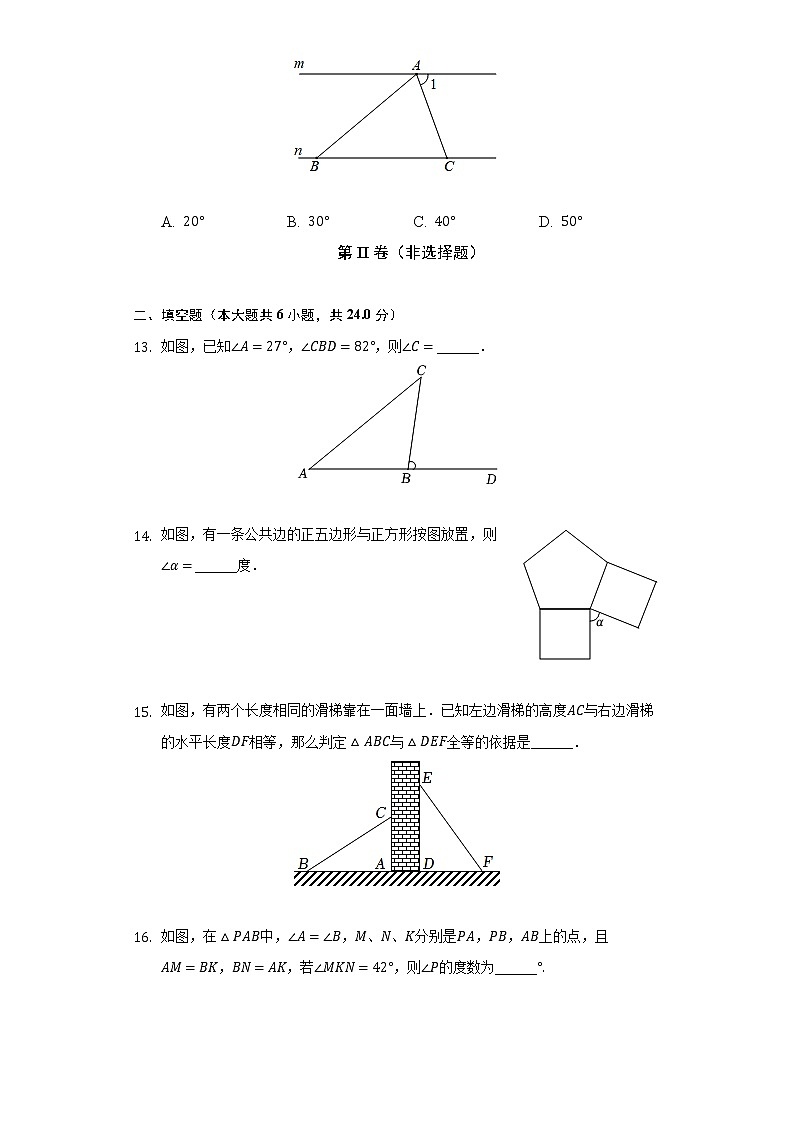
- 如图,直线,点在直线上,点,在直线上,,,那么等于( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共6小题,共24.0分)
- 如图,已知,,则______.
- 如图,有一条公共边的正五边形与正方形按图放置,则______度.
- 如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度与右边滑梯的水平长度相等,那么判定与全等的依据是______.
- 如图,在中,,、、分别是,,上的点,且,,若,则的度数为______
- 如图,在中,,,的垂直平分线交于点,交于点,,则的长为______.
- 如图,,点,分别在边,上,且,,点,分别在边,上,则的最小值是______.
三、解答题(本大题共8小题,共90.0分。解答应写出文字说明,证明过程或演算步骤)
- 本小题分
已知,,是的三边长.
若,,满足,试判断的形状;
化简:. - 本小题分
,两个村庄在如图所示的直角坐标系中,那么:
点的坐标为______,点的坐标为______;
在轴上有一条河,现准备在河流边上建一个抽水站,使得抽水站到、两个村庄的距离之和最小,请作出点的位置,并求此时距离之和的最小值.
- 本小题分
已知,如图,,,于.
与相等吗?为什么?
试说明是的高.
- 本小题分
如图,在中,,.
求证:;
若,,求的度数.
- 本小题分
如图,在中,是边上的中点,,,垂足分别为,,且求证:.
- 本小题分
如图,在中,,,,求的度数.
- 本小题分
计算:在平面直角坐标系中的位置如图所示.
作关于轴成轴对称的,并写出、、的坐标;
在轴上有一点,使的值最小,请在坐标系中标出点的位置.
- 本小题分
如图,在四边形中,与交于点,,;,,垂足分别为,.
求证:≌;
求证:.
答案和解析
1.【答案】
【解析】解:不是轴对称图形,故本选项不符合题意;
B.是轴对称图形,故本选项符合题意;
C.不是轴对称图形,故本选项不符合题意.
D.不是轴对称图形,故本选项不符合题意;
故选:.
根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.【答案】
【解析】解:全等三角形是指形状、大小相同的两个三角形,那么A错误,故A不符合题意.
B.全等三角形是指形状、大小相同的两个三角形,那么B错误,故B不符合题意.
C.全等三角形是指形状、大小相同的两个三角形,那么C错误,故C不符合题意.
D.全等三角形是指形状、大小相同的两个三角形,得全等三角形的周长、面积分别相等,那么D正确,故D符合题意.
故选:.
根据全等三角形的定义全等三角形是指形状、大小相同的两个三角形解决此题.
本题主要考查全等三角形,熟练掌握全等三角形的定义是解决本题的关键.
3.【答案】
【解析】解:由三角形的三边关系得:,
即,
只有不适合.
故选:.
根据三角形的三边关系,则第三根木条的取值范围是大于两边之差,而小于两边之和.
考查了三角形的三边关系,关键是根据三角形的三边关系得出范围解答.
4.【答案】
【解析】解:直线是中边的垂直平分线,
,
的周长,
当、、三点共线时,的周长最小,
,,,
的周长,
的周长最小值为,
故选:.
当、、三点共线时,的周长最小,最小值为的长.
本题考查轴对称求最短距离,熟练掌握轴对称求最短距离的方法是解题的关键.
5.【答案】
【解析】解:、三角形的外角大于与其不相邻的内角,故A说法错误;
B、三角形的外角中最多有个锐角,故B说法错误;
C、钝角三角形外角和等于,故C说法错误;
D、若三角形有一个外角为锐角,则这个三角形一定是钝角三角形,故D说法正确;
故选:.
据三角形的一个外角等于和它不相邻的两个内角的和;三角形内角和是分别进行分析即可.
此题主要考查了三角形的外角的性质,关键是掌握三角形的一个外角等于和它不相邻的两个内角的和.
6.【答案】
【解析】解:、,
,
,
是直角三角形,故选项不符合题意;
B、,
,
,
,
,
是直角三角形,故选项不符合题意;
C、,
设,
,,
,
,
解得,
不是直角三角形,故选项符合题意;
D、,
设,
,
,
,
解得,
,
是直角三角形,故选项不符合题意.
故选:.
根据三角形内角和定理和各选项中的条件计算出的内角,然后根据直角三角形的判定方法进行判断.
本题考查了三角形内角和定理以及直角三角形的判定,解题的关键是掌握三角形的内角和等于并灵活运用.
7.【答案】
【解析】解:一个四边形截去一个角后得到的多边形可能是三角形,可能是四边形,也可能是五边形,
内角和可能减少,可能不变,可能增加,
即新的多边形的内角和为或或.
故选:.
根据一个四边形截去一个角后得到的多边形的边数即可得出结果.
本题考查了多边形的内角与外角,能够得出一个四边形截去一个角后得到的图形有三种情形是解决本题的关键.
8.【答案】
【解析】解:点和点关于轴对称,
,,
解得,,
.
故选:.
依据点和点关于轴对称,即可得到,的值,进而得出结论.
本题主要考查了关于轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数,即点关于轴的对称点的坐标是.
9.【答案】
【解析】解:≌,,
,
故选:.
由全等三角形的对应边相等可求得答案.
本题主要考查全等三角形的性质,掌握全等三角形的对应边相等是解题的关键.
10.【答案】
【解析】解:在和中,
,
≌,
故选:.
根据全等三角形的判定定理求解即可.
此题考查了全等三角形的判定,熟记全等三角形的判定定理是解题的关键.
11.【答案】
【解析】解:是的平分线,,,
,
,
,
,
故选:.
先根据角平分线的性质得到,再利用三角形面积公式即可求解.
本题考查了角平分线的性质,熟记角的平分线上的点到角的两边的距离相等是解题的关键.
12.【答案】
【解析】解:,
,
,
,
,
故选:.
先由平行线的性质得出,根据等角对等边即可得出,根据三角形的内角和定理即可得到结论.
本题考查了平行线的性质,等腰三角形的判定以及三角形内角和定理,求出是解题的关键.
13.【答案】
【解析】解:是的外角,,,
.
故答案为:.
利用三角形的外角性质即可求解.
本题主要考查三角形的外角性质,解答的关键是明确三角形的外角等于与其不相邻的两个内角之和.
14.【答案】
【解析】解:正五边形的一个内角的度数是,正方形的一个内角的度数是,
所以,
故答案为:.
先求出正五边形和正方形的一个内角的度数,再求出答案即可.
本题考查了多边形内角与外角,能求出正五边形的一个内角的度数是解此题的关键.
15.【答案】
【解析】解:滑梯、墙、地面正好构成直角三角形,
在和中,
,
≌,
故答案为:.
根据,判断可出≌.
本题考查的是全等三角形的判定及性质,直角三角形的性质,属较简单题目.
16.【答案】
【解析】解:在和中,
,
≌,
,
是的外角,
,
,
,
,
故答案为:.
证明≌,根据全等三角形的性质得到,根据三角形的外角性质求出,根据三角形内角和定理计算,得到答案.
本题考查的是全等三角形的判定和性质、三角形的外角性质、三角形内角和定理,掌握全等三角形的判定定理是解题的关键.
17.【答案】
【解析】解:如图,连接,
在中,,,
,
是的垂直平分线,
,
,
,
,
.
故答案为:.
由在中,,,可求得的度数,又由的垂直平分线交于点,交于点,可得,即可得,又由含角的直角三角形的性质,求得答案.
此题考查了线段垂直平分线的性质以及含角的直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.
18.【答案】
【解析】解:作关于的对称点,作关于的对称点,连接,如图所示:
连接,即为的最小值.
根据轴对称的定义可知:,,
为等边三角形,为等边三角形,
,,,
在中,
.
故答案为:.
作关于的对称点,作关于的对称点,连接,即为的最小值;证出为等边三角形,为等边三角形,得出,由勾股定理求出即可.
本题考查了轴对称--最短路径问题,根据轴对称的定义,找到相等的线段,得到等边三角形是解题的关键.
19.【答案】解:,
或,
或或,
为等腰三角形或等边三角形;
解:,,是的三边长,
,,
原式
.
【解析】根据绝对值非负数的性质,得出或或,进而得出结论;
利用三角形的三边关系得到,,然后去绝对值符号后化简即可.
此题考查三角形的三边关系和三角形分类,利用三角形任意两边之和大于第三边,任意两边之差小于第三边,建立不等式解决问题.
20.【答案】解:,;
作点关于轴的对称点,连接交轴于点,
则点就是使得抽水站到两个村庄的距离之和最小,即最小,
的长度即为的最小值,所以的最小值.
【解析】本题考查的是轴对称最短路线问题以及勾股定理的运用,熟知“两点之间线段最短”是解答此题的关键.
根据图象即可得到答案;
先求出点关于轴的对称点的坐标,连接交轴于点,此时最小,然后根据勾股定理即可得到结论.
解:点的坐标为,点的坐标为,
故答案为:,;
见答案.
21.【答案】解:,
理由如下:,
,
;
,,
,
,
,
,即是的高.
【解析】根据同位角相等,两直线平行得到,再根据两直线平行,内错角相等证明结论;
根据平行线的性质得到,根据三角形的高的概念证明即可.
本题考查的是平行线的判定和性质、三角形的高的概念,掌握平行线的判定定理是解题的关键.
22.【答案】解:,理由如下:
,
,
,
,
,
;
,,
,
,,
,
.
【解析】由于,可判断,则,由得出判断出;
由,得到,由得出,得出的度数.
本题考查了平行线的判定与性质:内错角相等,两直线平行;两直线平行,同位角相等,同旁内角互补.
23.【答案】证明:,,
,
是上的中点,
,
在和中,
,
≌,
.
【解析】根据证明≌,根据全等三角形的性质即可得证.
本题考查了全等三角形的判定和性质,熟练掌握直角三角形特有的判定方法是解题的关键.
24.【答案】解:,
,
,
,
,
,
.
【解析】根据等边对等角,得出,知道了顶角,求出底角;再根据,得到,最后根据即可求解.
本题考查了等腰三角形的性质,平行线的性质,熟练掌握等腰三角形的性质定理是解题的关键.
25.【答案】解:如图,,,,;
如图,点即为所求.
【解析】利用轴对称变换的性质分别作出,,的对应点,,即可;
连接交轴于点,连接,点即为所求.
本题考查作图轴对称变换,轴对称最短问题等知识,解题的关键是掌握轴对称变换的性质,属于中考常考题型.
26.【答案】证明:于点,于点,
,,
在和中,
,
≌.
证明:,
,
,
在和中,
,
≌,
.
【解析】先由于点,于点证明,即可根据全等三角形的判定定理“”证明≌;
先由证明,而,即可根据全等三角形的判定定理“”证明≌,得.
此题重点考查全等三角形的判定与性质,正确地找到全等三角形的对应边和对应角是解题的关键.
四川省绵阳市涪城区2023-2024学年八年级上学期开学考试数学试卷(含答案): 这是一份四川省绵阳市涪城区2023-2024学年八年级上学期开学考试数学试卷(含答案),共6页。试卷主要包含了下列说法错误的是,下列命题是真命题的是,若m>n,则下列各式中正确的是,9%等内容,欢迎下载使用。
+四川省绵阳市涪城区2023-2024学年八年级上学期开学数学试卷: 这是一份+四川省绵阳市涪城区2023-2024学年八年级上学期开学数学试卷,共23页。试卷主要包含了选择题.,填空题,解答题等内容,欢迎下载使用。
2022-2023学年四川省绵阳市涪城区八年级(下)期中数学试卷(含解析): 这是一份2022-2023学年四川省绵阳市涪城区八年级(下)期中数学试卷(含解析),共22页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












