湖南省常德市安乡县2022-2023学年九年级上学期期中质量监测数学试题(含答案)

安乡县2022年下学期期中质量监测九年级数学试题卷

时量：120分钟      分值;120分     命题人：

一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置

1．下列各组中的四条线段成比例的是（     ）

A．，，，            B．，，，

C．，，，            D．，，，

2.把方程化成的形式，则=（    ）

A．-15          B．9           C．15            D．6

3.不解方程，判断方程的根的情况（    ）

A.有两个不相等的实根               B.有两个相等的实根

C.无实根                           D.无法确定

4.如下图,在中,,,,将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是（     ）

A．B．C． D．

5．已知反比例函数,下列结论中不正确的是（    ）

A．其图像分别位于第二、四象限。            B．其图像关于原点对称。

C．其图像经过点(2，-4)。 D．若点都在图像上，且＜，则＜

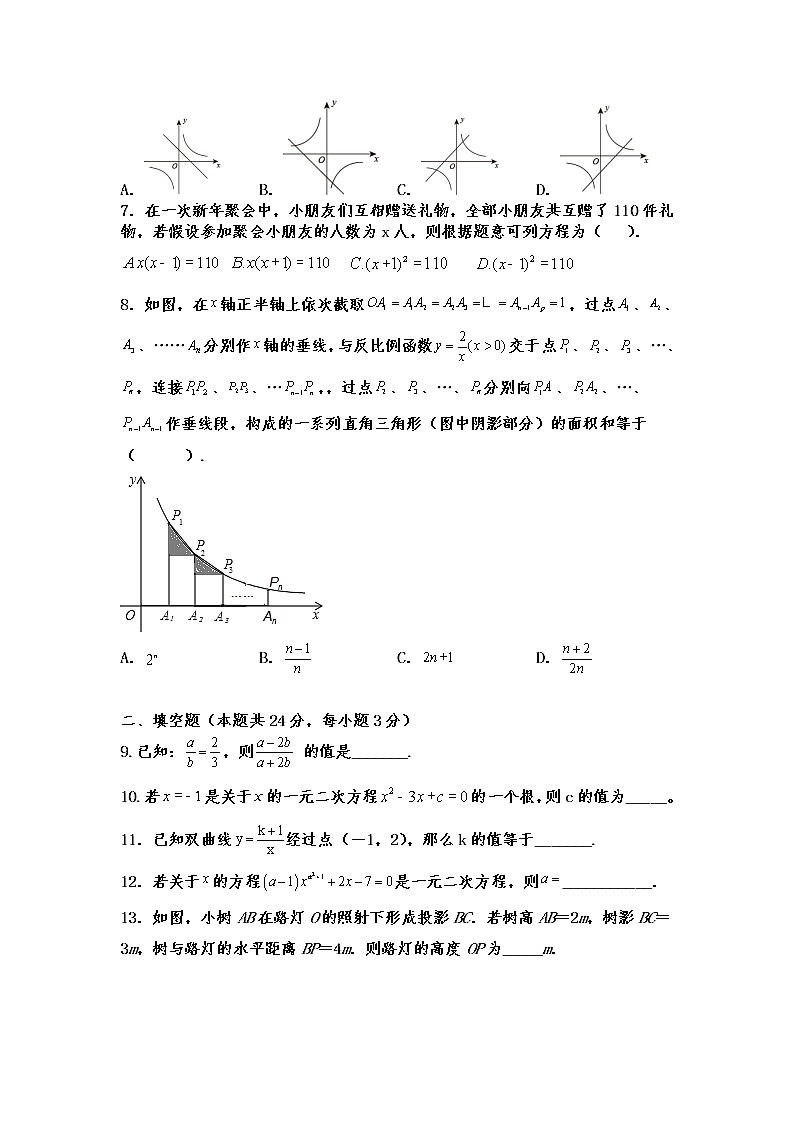
6．在同一平面直角坐标系中，函数和的图象大致是（   ）

A． B． C． D．

7．在一次新年聚会中，小朋友们互相赠送礼物，全部小朋友共互赠了110件礼物，若假设参加聚会小朋友的人数为x人，则根据题意可列方程为（   ）．

8．如图，在轴正半轴上依次截取，过点、、、……分别作轴的垂线，与反比例函数交于点、、、…、，连接、、…，，过点、、…、分别向、、…、作垂线段，构成的一系列直角三角形（图中阴影部分）的面积和等于（    ）.

A． B． C． D．

二、填空题（本题共24分，每小题3分）

9.已知：，则 的值是_______.

10.若是关于的一元二次方程的一个根，则c的值为_____。

11．已知双曲线经过点（－1，2），那么k的值等于_______.

12．若关于的方程是一元二次方程，则___________．

13．如图，小树AB在路灯O的照射下形成投影BC．若树高AB＝2m，树影BC＝3m，树与路灯的水平距离BP＝4m．则路灯的高度OP为_____m．

14．反比例函数图象的一支如图所示,的面积为2,则该函数的解析式是_______

15．如图，P为平行四边形ABCD的边AD上的一点，E，F分别为PB，PC的中点，△PEF，△PDC，△PAB的面积分别为S，，．若S=3，则的值为______

16．将三角形纸片(△ABC)按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF．已知AB＝AC＝3，BC＝4，若以点B′，F，C为顶点的三角形与△ABC相似，则BF的长度是________．

三、解答题（本题9个小题，共72分）

17.解方程：（本题2小题，每题5分，共10分） 

       （2）  .

18（本题满分6分）如图，在△ABC中，已知，AD=4，DB=8，DE=3．

 （1）求的值；       (2)求BC的长       

19.（本题满分6分）已知反比例函数 的图像经过．

(1)求k的值．

(2)判断点是否在这个函数的图像上，并说明理由

20.（本题满分7分）已知关于x的一元二次方程x2+（2k﹣1）x+k（k+1）＝0（k是常量），它有两个不相等的实数根．

(1)求k的取值范围；

(2)当﹣2＜k＜3，且k为整数时，求原方程的解．

21（本题满分7分）为满足师生阅读需求，某校图书馆的藏书量不断增加，2019年年底的藏书量为5万册，2021年年底的藏书量为7.2万册.

(1)求该校这两年藏书的年均增长率；

(2)假设2022年该校藏书的年均增长率与前两年相同，请你预测到2022年年底该校的藏书量是多少？

22（本题满分8分）如图，在等边中，D为边上一点，E为边上一点，，，．

(1)求证：；

(2)求的边长．

23（本题满分8分）已知在直角坐标系中，菱形ABDC，顶点A(0，4)，B(-3，0)，点D在x轴负半轴，求：

(1)求点D的坐标，

(2)求经过点C的反比例函数解析式．

24（本题满分10分）阅读材料：

材料1：若关于的一元二次方程的两个根为，，则，.

材料2：已知一元二次方程的两个实数根分别为m，n，求的值.

解：∵一元二次方程的两个实数根分别为m，n，

∴，，则.

根据上述材料，结合你所学的知识，完成下列问题：

(1)材料理解：一元二次方程的两个根为，，则___________，___________.

(2)类比应用：已知一元二次方程的两根分别为m、n，求的值.

(3)思维拓展：已知实数s、t满足，，且，求的值.

25.（本题满分10分）如图，分别与x轴，y轴交于A，B，与反比例（x＞0）相交于第一象限内的点P（2，），作PC⊥x轴于点C．

(1)求双曲线的表达式．

(2)在（1）所求的双曲线上是否存在点Q（m，n）其中m＞0，作QH⊥x轴于H，使得QCH与AOB相似？若存在，求出点Q坐标，若不存在，说明理由．

安乡县2022年下学期期中质量监测九年级数学参考答案

一、选择题（本题共24分，每小题3分）

BCBC     DCAB

四、填空题（本题共24分，每小题3分）

9.    10.-4      11.-3         12.-1     13.

14..     15. 12          16.2或

五、解答题（10小题，共72分）

17.解方程：（本题2小题，每题5分，共10分） 

解：

，……………………1分

，……………………2分

，……………………4分

解得：，；……………………5分（用其它方法酌情给分）

.

解：，

，……………………1分

，……………………3分

解得：.……………………5分（用其它方法酌情给分）

18.（本题满分6分）（1）解：∵AD=4，DB=8

∴AB=AD+DB=4+8=12……………………1分

∴；……………………3分

（2）∵

∴△ADE∽△ABC……………………4分

∴……………………5分

∵DE=3    ∴

∴BC=9．……………………6分

19．（本题满分6分）（1）解：反比例函数 的图像经过，

，

；……………………3分

（2）把代入反比例函数，

得：，

点不在这个函数的图像上．……………………6分

20.（本题满分7分）（1）解：

=，

解得： ．

故k的取值范围是；……………………3分

（2）解：∵﹣2＜k＜3，且k为整数，

∴k＝﹣1或0，……………………5分

当k＝﹣1时，方程；

解得它的两根为x1＝0，x2＝3；……………………6分

当k＝0时，方程，

解得它的两根为x1＝0，x2＝1．……………………7分

21.（本题满分7分）（1）设该校这两年藏书的年均增长率为x，

根据题意，得……………………3分

解得，（不合题意，舍去）

该校这两年藏书的年均增长率为20%；……………………5分

（2）（万册），

所以，预测到2022年年底该校的藏书量是8.64万册.……………………7分

22．（本题满分8分）（1）证明：∵△ABC是等边三角形，

∴∠B=∠C=60°．

∵∠ADC=∠B+∠BAD，

∴∠ADE+∠EDC=∠B+∠BAD，

∵∠B=∠ADE=60°，

∴∠BAD=∠EDC．

∵∠B=∠C=60°，

∴．……………………4分

（2）解：∵，

∴，

设AB=x，则CD=BC－BD= AB－BD=x－4，

∴，

解得：x=16，

经检验：x=16是方程的解，

∴AB的长为16．……………………8分

23．（本题满分8分）（1）如图，

∵顶点A(0，4)，B(-3，0)，

∴，

∴DB=AB=5，

∴OD=5+3=8，

∴D(-8，0)；……………………4分

（2）如图，过点C作CE⊥x轴．

∵在菱形ABDC中，CE=OA=4，OE=AC=5，

∴点C(-5，4)．

设反比例函数解析式为，

∵点C(-5，4)在反比例函数上，

∴k=xy=-20，

∴经过点C的反比例函数解析式为．……………………8分

24.（本题满分10分）（1）解：∵一元二次方程的两个根为，，

∴，．

故答案为：；．……………………2分（每空1分）

（2）∵一元二次方程的两根分别为m、n，

∴，，

∴……………………3分

……………………4分

；……………………5分

（3）∵实数s、t满足，，

∴s、t可以看作方程的两个根，

∴，，……………………6分

∵

……………………8分

∴或，

当时，

，……………………9分

当时，

，

综上分析可知，的值为或．……………………10分

25．（本题满分10分）（1）∵点P（2，）在直线上，

∴=×2+2=3，

∴点P（2，3），

∴3=，    解得k=6，……………………4分

∴双曲线的解析式为y=（x＞0）；

（2）解：如图，

当x=0时，，

当y=0时，，x=-4，

∴A（﹣4，0），B（0，2）

∴OA=4，OB=2，

∵Q（m，n）在双曲线y=上

∴，

当Q在P右侧时，

当AOB∽CHQ时，

=

即=

m=或m=舍去

∴Q（，）……………………7分

当AOB∽QHC时，

，即

解得m=3或－2（舍弃），

∴Q（3，2），

②当Q在P左侧时，同法可得，Q不存在．

∴Q（，）或（3，2）．……………………10分