初中数学华师大版八年级上册2 作一个角等于已知角图片ppt课件

这是一份初中数学华师大版八年级上册2 作一个角等于已知角图片ppt课件，共25页。PPT课件主要包含了新课导入，数学家欧几里得，探究新知，3作射线OC，1作直线AB，AD就是要求作的高，2作直线CD，线段AB的中点，①找线段中点，课堂小结等内容，欢迎下载使用。

用圆规和直尺能不能作出正七边形、正九边形、正十一边形、正十三边形、正十七边形呢?
两千年来，这一直是个未解之谜.
出乎人意料之外的是，这个难题竞被年仅19岁的高斯解决了. 他用直尺和圆规作出了正十七边形.
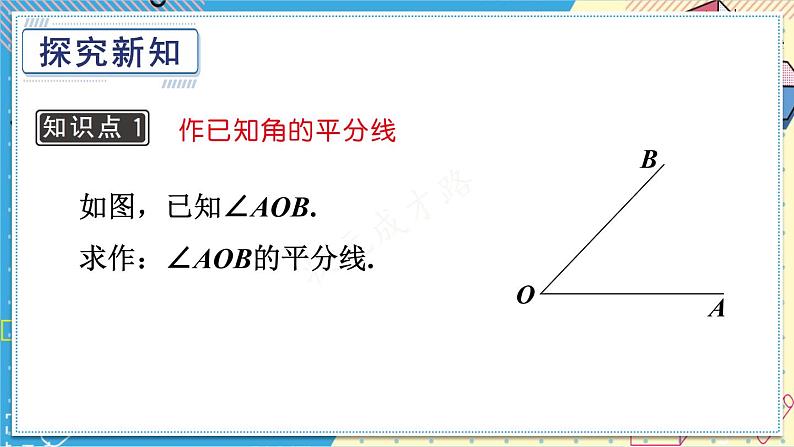
如图，已知∠AOB.求作：∠AOB的平分线.
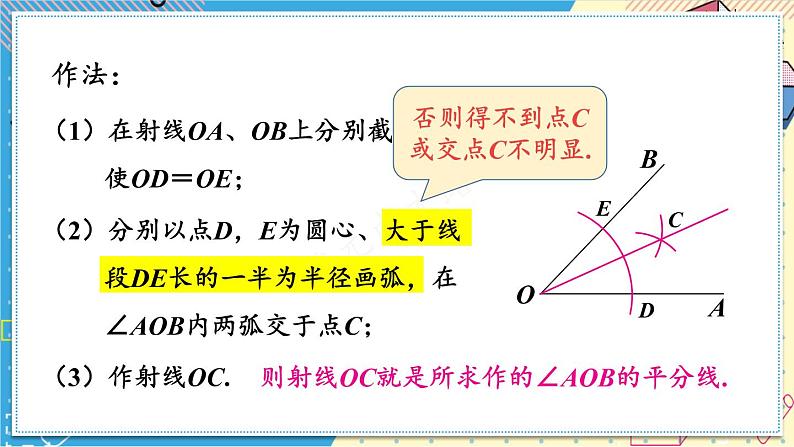
（1）在射线OA、OB上分别截取OD、OE，使OD＝OE；
（2）分别以点D，E为圆心、大于线段DE长的一半为半径画弧，在∠AOB内两弧交于点C；
则射线OC就是所求作的∠AOB的平分线.
否则得不到点C或交点C不明显.
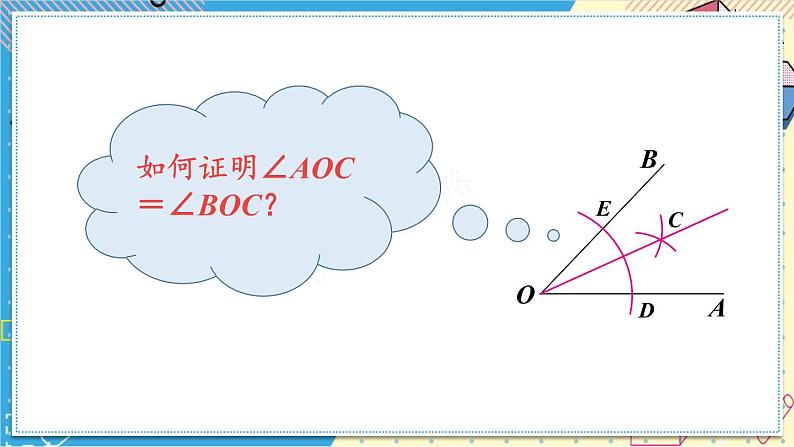
如何证明∠AOC＝∠BOC？
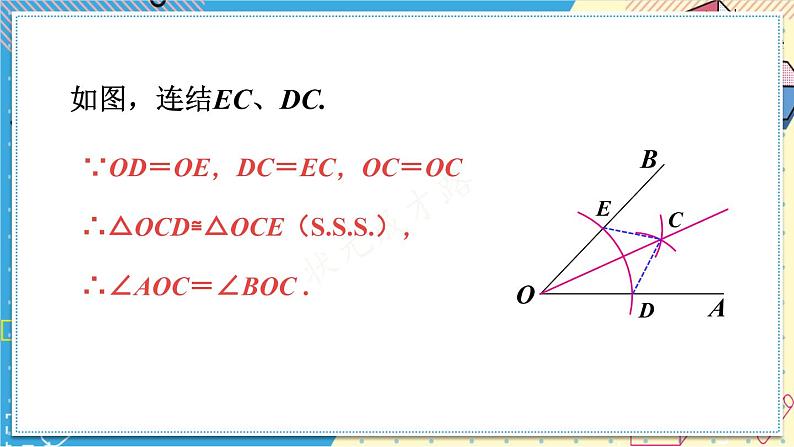
如图，连结EC、DC.
∵OD＝OE，DC＝EC，OC＝OC
∴△OCD≌△OCE（），
∴∠AOC＝∠BOC .
2. 做出图中三角形的三个角的平分线。
如何过一点 C 作已知直线 AB 的垂线呢？
点C与已知直线 AB 的位置关系有两种：点C在直线 AB 上或点C在直线 AB 外.
（1）当点 C 在直线 AB 上
① 做平角ACB的平分线CD；
② 反向延长射线CD.
直线CD就是要求作的垂线.
（2）当点 C 在直线 AB 外
① 以点C为圆心，作能与直线AB相交于D、E两点的弧；
②作∠DCE的平分线.
直线CF就是要求作的垂线.
△CDE为等腰三角形. 由“三线合一”可知，只需作出∠DCE的平分线，则该平分线所在的直线就是要求作的垂线.
利用直尺和圆规作一个等于45°的角.
（2）过点A作直线AB的垂线AC；
（3）作∠CAB的平分线AD.
∠DAB就是要求作的角.
1. 如图，点P在∠O的一边上，试过点P作该角两边的垂线.
2. 如图，作△ABC边BC上的高.
CA＝CB，DA＝DB
由此，你能发现作垂直平分线的方法吗?
已知：如图，线段AB.求作：线段AB的垂直平分线CD.
（1）分别以点A和点B为圆心、大于AB一半的长为半径作圆弧，两弧相交于点C和点D；
直线CD就是要求作的线段AB的垂直平分线.
如何证明直线CD垂直平分线段AB？
如图，连结CA、CB、DA、DB.
∵AC＝BC，AD＝BD，CD＝CD，
∴△ACD≌△BCD（），
∴∠ACD＝∠BCD .
∴CD垂直平分线段AB（等腰三角形的“三线合一”）.
②作任意三角形的三边的中线
1. 四等分已知线段AB.
2.如图，作△ABC的边BC的垂直平分线.
直线EF就是要求作的垂直平分线.
（1）以已知角的顶点为圆心、适当长为半径作弧交已知角的两边于两点
（2）再分别以这两个交点为圆心、大于这两点的距离的一半为半径作弧，两弧交于一点
（3）以已知角的顶点为顶点过两弧交点作射线,射线就是已知角的平分线