资料中包含下列文件，点击文件名可预览资料内容

课件

4.3 逻辑图与逻辑代数的运算律课件-高二下学期高教版中职数学职业模块工科类.ppt
教案

4.3 逻辑图与逻辑代数的运算律教案-高二下学期高教版中职数学职业模块工科类.doc

还剩7页未读，继续阅读

下载需要20学贝 1学贝=0.1元

使用下载券免费下载

加入资料篮

立即下载

所属成套资源：高教版（中职）数学职业模块工科类课件PPT+教案整套

成套系列资料，整套一键下载

浏览整套资料 (共24份)

高教版（中职）职业模块工科类4.3.2 逻辑代数的运算律精品ppt课件

展开

这是一份高教版（中职）职业模块工科类4.3.2 逻辑代数的运算律精品ppt课件，文件包含43逻辑图与逻辑代数的运算律课件-高二下学期高教版中职数学职业模块工科类ppt、43逻辑图与逻辑代数的运算律教案-高二下学期高教版中职数学职业模块工科类doc等2份课件配套教学资源，其中PPT共14页，欢迎下载使用。

【课题】 4.3　逻辑图与逻辑代数的运算律

【教学目标】

知识目标：

（1）理解逻辑函数的概念，掌握逻辑函数的表示法．

（2）会画逻辑函数的逻辑图．

（3）了解逻辑代数的运算律及利用运算律化简逻辑式．

能力目标：

通过对逻辑式化简的学习，使学生的数学思维能力得到锻炼和提高．

【教学重点】

（1）逻辑函数与逻辑图．

（2）逻辑代数的运算律．

【教学难点】

（1）逻辑图．

（2）用运算律化简逻辑式．

（3）掌握逻辑门的符号．

【教学设计】

数字逻辑电路是计算机、电工电子等专业的专业课程，它是建立在逻辑代数的基础上．正确把握逻辑表达式、逻辑图、真值表之间的关系是分析数字逻辑电路的基础，而逻辑表达式、逻辑图、真值表之间的相互换算是数字逻辑电路的主要任务之一．因此，让学生掌握逻辑图与逻辑代数运算律的相关知识非常必要．逻辑函数是反映逻辑变量之间关系的函数．写法上与普通函数相类似，逻辑函数一般用逻辑式来表示，这个逻辑式叫做逻辑函数的表达式．例1是逻辑电路图的知识巩固性题目，教学中要强调画出逻辑电路图的步骤和方法，注意逻辑运算的优先次序；强调输入端和输出端．教学中要首先分析逻辑表达式，明确逻辑关系，然后再结合基本门电路符号画出逻辑图．利用运算律化简逻辑式不要要求过高，这里需要许多运算技巧，学生不可能短时间内掌握．教学重点是认识化简前后逻辑式，看到逻辑式化简的好处．了解化简的基本步骤，明确逻辑表达式中的项数最少和变量出现的次数最少是化简完成的目标．例2是感知利用运算律化简逻辑式的新知识介绍性题目．

【教学备品】

教学课件．

【课时安排】

2课时．(90分钟)

【教学过程】

教学

过程

教师

行为

学生

行为

教学

意图

时间

*揭示课题

4.3逻辑图与逻辑代数的运算律

介绍

了解

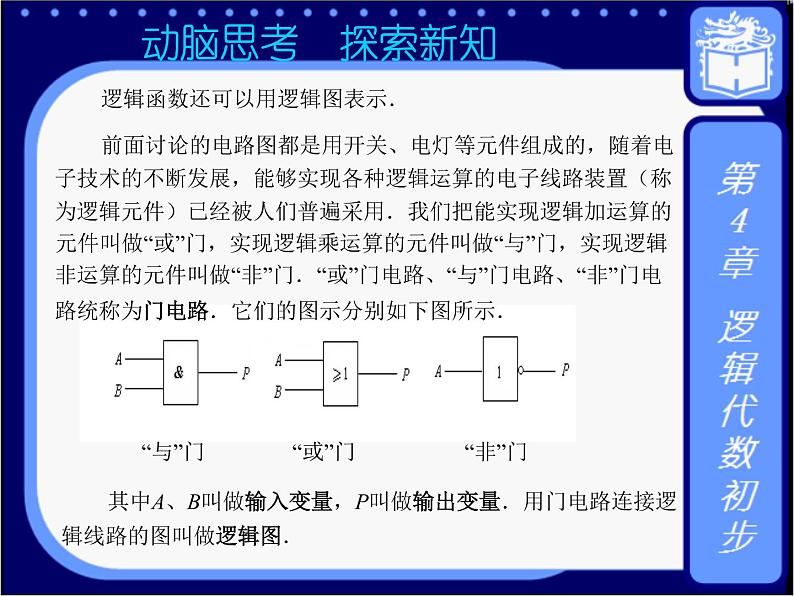
*动脑思考探索新知

4.3.1 逻辑函数与逻辑图

反映逻辑变量之间关系的函数叫做逻辑函数．逻辑函数中的自变量是逻辑变量，取值范围为1和0．与普通代数相类似，逻辑函数可以写作，其中，逻辑变量A、B、C为自变量，逻辑变量Y为因变量的函数．

用“逻辑加”、“逻辑乘”、“逻辑非”等运算表示函数与各个变量间逻辑关系的式子叫做逻辑函数的表达式．例如，

．

逻辑函数还可以用逻辑图表示．

前面讨论的电路图都是用开关、电灯等元件组成的，随着电子技术的不断发展，能够实现各种逻辑运算的电子线路装置（称为逻辑元件）已经被人们普遍采用．我们把能实现逻辑加运算的元件叫做“或”门，实现逻辑乘运算的元件叫做“与”门，实现逻辑非运算的元件叫做“非”门．“或”门电路、“与”门电路、“非”门电路统称为门电路．它们的图示分别如图4－5中的（1）、（2）、（3）所示．

图4−5

其中A、B叫做输入变量，P叫做输出变量．用门电路连接逻辑线路的图叫做逻辑图．

详细分析讲解

总结

归纳

详细分析讲解

思考

理解

记忆

理解

记忆

带领

学生

总结

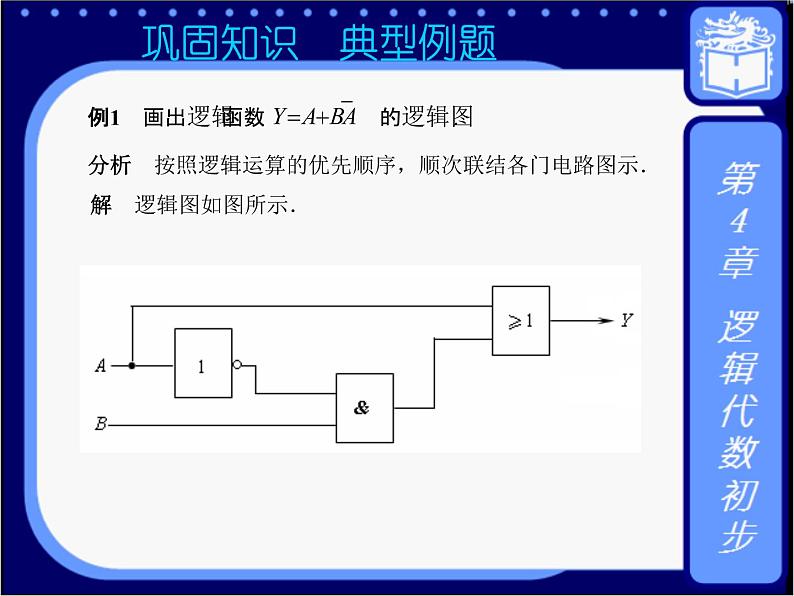
*巩固知识典型例题

例1 画出逻辑函数的逻辑图．

分析按照逻辑运算的优先顺序，顺次联结各门电路图示．

解逻辑图如图4－6所示．

图4−6

引领

讲解

说明

观察

思考

主动

求解

通过

例题

进一

步领

会

*运用知识强化练习

1．画出的逻辑图．

2．画出的逻辑图．

提问

巡视

指导

动手

求解

了解

学生

知识

掌握

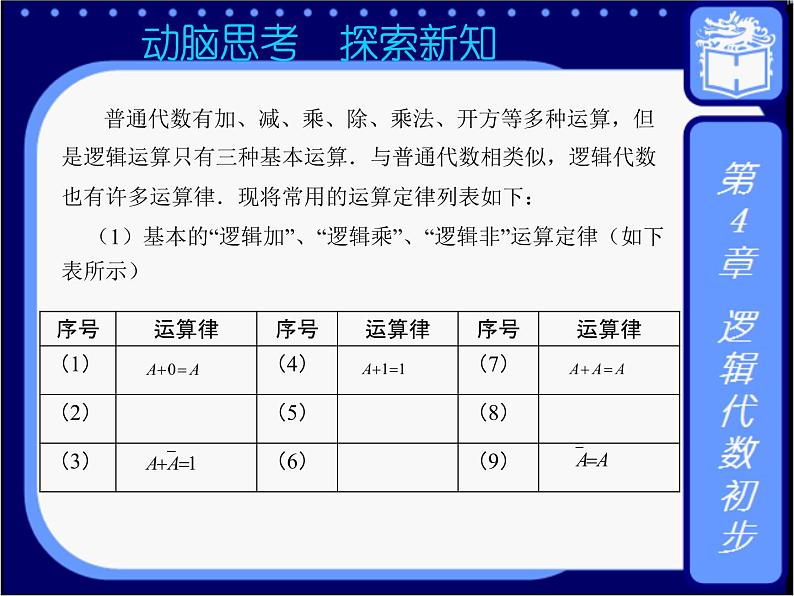
*动脑思考探索新知

4.3.2 逻辑代数的运算律

普通代数有加、减、乘、除、乘法、开方等多种运算，但是逻辑运算只有三种基本运算．与普通代数相类似，逻辑代数也有许多运算律．现将常用的运算定律列表如下：

（1）基本的“逻辑加”、“逻辑乘”、“逻辑非”运算定律（如表4-9所示）

序号	运算律	序号	运算律	序号	运算律
（1）		（4）		（7）
（2）		（5）		（8）
（3）		（6）		（9）

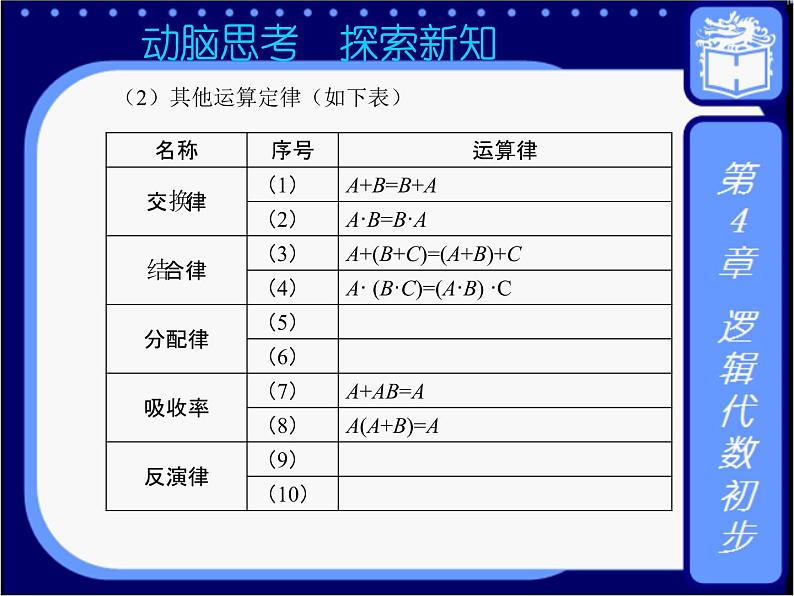
表4-9

（2）其他运算定律（如表4-10）

名称	序号	运算律
交换律	（1）	A+B=B+A
交换律	（2）	A·B=B·A
结合律	（3）	A+(B+C)=(A+B)+C
结合律	（4）	A· (B·C)=(A·B) ·C
分配律	（5）
分配律	（6）
吸收率	（7）	A+AB=A
吸收率	（8）	A(A+B)=A
反演律	（9）
反演律	（10）

表4-10

上述运算律可以通过真值表进行验证．利用这些运算律可以化简逻辑式．化简逻辑式一般要完成下面几个步骤：

（1）将被加项中的括号去掉；

（2）使被加项的项数最少；

（3）基本逻辑变量出现的次数最少．

详细分析讲解

总结

归纳

分析讲解

思考

理解

记忆

理解

记忆

带领

学生

总结

*巩固知识典型例题

例2 化简：（1）； (2)

解　（1）（反演律）

　　（结合律）

；（基本运算律7）

(2) （反演律）

（反演律）

（基本运算律4）

．（基本运算律5）

引领

讲解

说明

观察

思考

主动

求解

通过

例题

进一

步领

会

*运用知识强化练习

1. 用真值表证明下列各式：

（1）A+1=1 ；（2）；（3）A(A+B)=A．

2. 化简下列逻辑式．

提问

巡视

指导

动手

求解

及时

了解

学生

知识

掌握

*理论升华整体建构

思考并回答下面的问题：

化简逻辑式一般要完成哪些步骤？

结论：

化简逻辑式一般要完成下面几个步骤：

（1）将被加项中的括号去掉；

（2）使被加项的项数最少；

（3）基本逻辑变量出现的次数最少．

质疑

强调

回答

强化

师生共同归纳强调重点

*归纳小结强化思想

本次课学了哪些内容？重点和难点各是什么？

引导

回忆

*自我反思目标检测

本次课采用了怎样的学习方法？你是如何进行学习的？你的学习效果如何？

化简下列逻辑式．

提问

巡视

指导

反思

动手

求解

检验

学习

效果

*继续探索活动探究

(1)读书部分：教材

(2)书面作业：教材习题4．3（必做）；学习与训练训练题4．3（选做）

(3)实践调查：编写一道逻辑式化简问题并求解

说明

记录

分层次要求

【教师教学后记】

项目	反思点
学生知识、技能的掌握情况	学生是否真正理解有关知识；是否能利用知识、技能解决问题；在知识、技能的掌握上存在哪些问题；
学生的情感态度	学生是否参与有关活动；在教学活动中，是否认真、积极、自信；遇到困难时，是否愿意通过自己的努力加以克服；
学生思维情况	学生是否积极思考；思维是否有条理、灵活；是否能提出新的想法；是否自觉地进行反思；
学生合作交流的情况	学生是否善于与人合作；在交流中，是否积极表达；是否善于倾听别人的意见；
学生实践的情况	学生是否愿意开展实践；能否根据问题合理地进行实践；在实践中能否积极思考；能否有意识的反思实践过程的方面；