初中数学北师大版八年级上册第六章 数据的分析1 平均数教学课件ppt

这是一份初中数学北师大版八年级上册第六章 数据的分析1 平均数教学课件ppt，共21页。PPT课件主要包含了导入新课，探究新知，归纳总结，应用举例，课堂小结，平均数，算术平均数，加权平均数，随堂练习等内容，欢迎下载使用。

在篮球比赛中,队员的身高、年龄都是影响球队实力的因素，如何衡量两个球队队员的身高？怎样理解“甲队队员的身高比乙队更高”?怎样理解“甲队队员比乙队更年轻”？
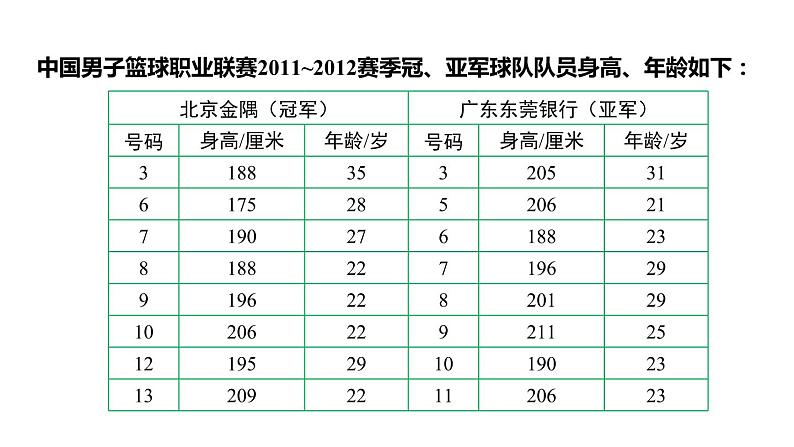
中国男子篮球职业联赛2011~2012赛季冠、亚军球队队员身高、年龄如下：
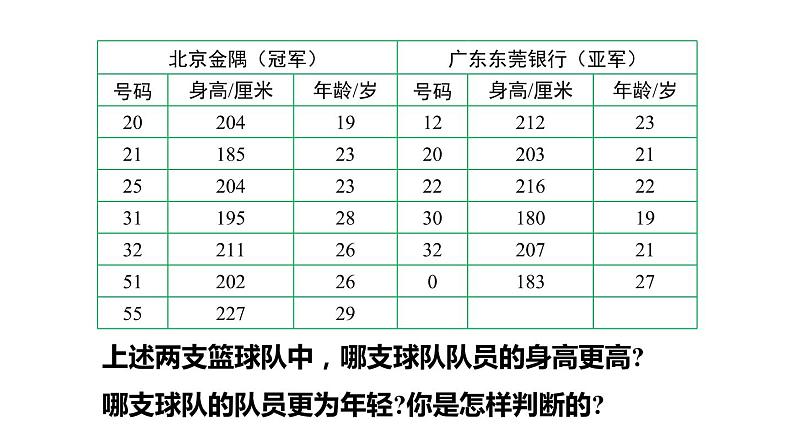
上述两支篮球队中，哪支球队队员的身高更高?哪支球队的队员更为年轻?你是怎样判断的?
怎样求一组数据的平均数呢？
问题1：上述两支篮球队中，哪支球队队员的身高更高？我们可以用____________表示这组数据的“平均水平”．
解：金隅队平均身高：(188＋175＋…＋202＋227)÷____≈____(cm)；东莞银行队平均身高：(205＋206＋…207＋183)÷____≈____(cm).
问题2：怎样计算他们的平均年龄？解：金隅队平均年龄：(35＋28＋27＋22＋…＋26＋29)÷____＝____(岁)；东莞银行队平均年龄：(31＋21＋23＋…＋21＋27)÷____≈____(岁)．
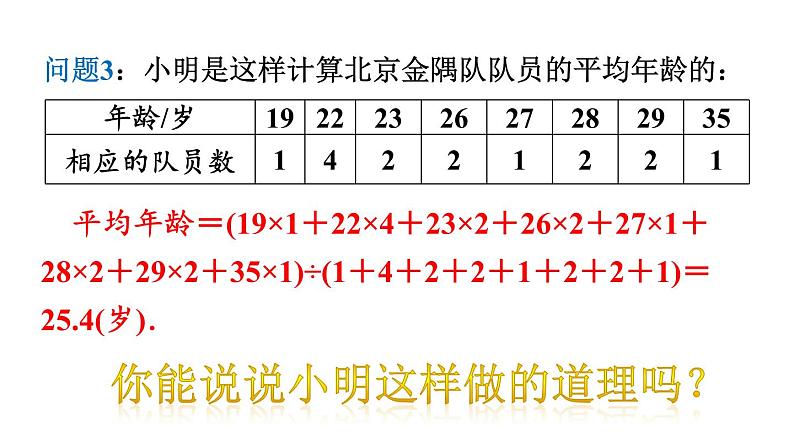
问题3：小明是这样计算北京金隅队队员的平均年龄的：
　平均年龄＝(19×1＋22×4＋23×2＋26×2＋27×1＋28×2＋29×2＋35×1)÷(1＋4＋2＋2＋1＋2＋2＋1)＝25.4(岁)．
你能说说小明这样做的道理吗？
某校在一次会操比赛中八(1)班、八(2)班、八(3)班、八(4)班的成绩如下(单位：分)：
评分规则1：根据三项得分的平均成绩从高到低确定名次．(除不尽的四舍五入保留一位小数)评分规则2：学校认为这三个项目的重要程度有所不同，将领操员、服装统一、动作整齐三项得分按1∶2∶2的比例确定各班的成绩．
实际问题中，一组数据里的各个数据的“重要程度”未必相同．因而，在计算这组数据的平均数时，往往给每个数据一个“权”．例如，上题中1，2，2 分别是领操员、服装统一、动作整齐三项成绩的“权”．而 称为八(1)班三项成绩的加权平均数．
例1 某广告公司欲招聘广告策划人员一名，对A、B、C候选人进行了三项素质测试.他们的各项测试成绩如下表所示:
（1）如果根据三项测试的平均成绩决定录用人选，那么谁将被录用？
（2）根据实际需要，公司将创新、综合知识和语言三项测试得分按4∶3∶1的比例确定各人的测试成绩，此时谁将被录用？
（1）A的平均成绩为（72+50+88）/3=70(分).
B的平均成绩为（85+74+45）/3=68(分).
C的平均成绩为（67+70+67）/3=68(分).
由70>68，故A被录用.
因此候选人B将被录用.
4，3，1 分别是创新、综合知识、语言三项测试成绩的权，而称（72×4+50×3+88×1）÷（4+3+1）为A的三项测试成绩的加权平均数.
例2 某市广播电视局欲招聘播音员一名，对A，B两名候选人进行了两次素质测试，两人的两次测试成绩(百分制)如下表所示：
　根据实际需要，广播电视局将面试、综合知识测试的得分按3∶2的比例计算两人的总成绩，那么____(选填“A”或“B”)将被录用．
1. 某次体操比赛，六位评委对某位选手的打分（单位：分）如下：
（1）求这六个分数的平均分；
（2）如果规定：去掉一个最高分和一个最低分，余下分数的平均值作为这位选手的最后得分，那么该选手的最后得分是多少？
2. 某校规定学生的体育成绩由三部分组成：早锻炼及体育课外活动表现占成绩的20%，体育理论测试占30%，体育技能测试占50%.小颖的上述三项成绩依次是：92分，80分，84分，则小颖这学期的体育成绩是多少？