2022秋高中数学章末素养提升6第六章计数原理课件新人教A版选择性必修第三册

这是一份2022秋高中数学章末素养提升6第六章计数原理课件新人教A版选择性必修第三册，共31页。

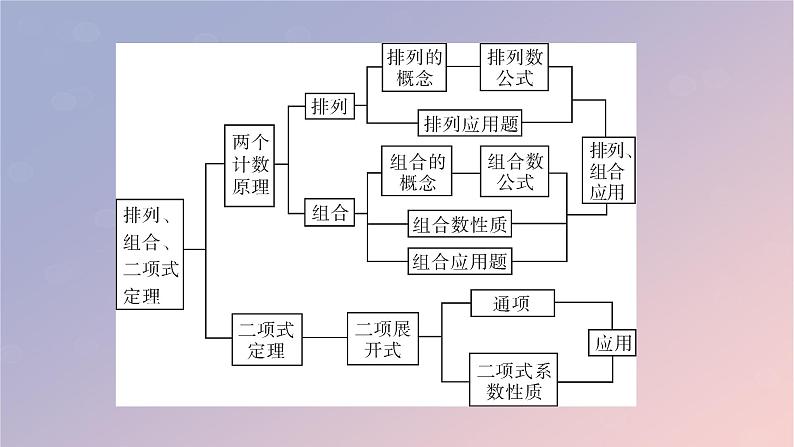
第六章　计数原理章末素养提升| 体系构建 || 核心归纳 |1．两个计数原理分类加法计数原理与分步乘法计数原理是排列组合中解决问题的重要手段，也是基础方法，尤其是分类加法计数原理与分类讨论有很多相通之处，当遇到比较复杂的问题时，用分类的方法可以有效的将之分解，达到求解的目的．正确地分类与分步是用好两个原理的关键，即完成一件事到底是“分步”进行还是“分类”进行，这是选用计数原理的关键．2．排列与组合排列数与组合数计算公式主要应用于求值和证明恒等式，其中求值问题应用连乘的形式，证明恒等式应用阶乘的形式，在证明恒等式时，要注意观察恒等式左右两边的形式，基本遵循由繁到简的原则，有时也会从两边向中间靠拢．对于应用题，则首先要分清是否有序，即是排列问题还是组合问题．3．排列数与组合数公式及性质| 思想方法 |(一)分类讨论思想【方法解读】解含有约束条件的排列、组合问题，应按元素的性质进行分类，分类时需要满足两个条件：①类与类之间要互斥(保证不重复)；②总数要完备(保证不遗漏)． 车间有11名工人，其中5名男工是钳工，4名女工是车工，另外两名老师傅既能当车工又能当钳工，现在要在这11名工人里选派4名钳工，4名车工修理一台机床，则有多少种选派方法？解：方法一　设A，B代表2位老师傅．A，B都不在内的选派方法有CC＝5(种)，A，B都在内且当钳工的选派方法有CCC＝10(种)，A，B都在内且当车工的选派方法有CCC＝30(种)，A，B都在内且一人当钳工，一人当车工的选派方法有ACC＝80(种)，A，B有一人在内且当钳工的选派方法有CCC＝20(种)，A，B有一人在内且当车工的选派方法有CCC＝40(种)，所以选派方法共有5＋10＋30＋80＋20＋40＝185(种)．【点评】本题主要考查排列组合的综合问题，解决本题的关键是对特殊要求元素“两名老师傅既能当车工又能当钳工”进行分类讨论．1．从1,2,3,4,5,6这6个数字中，任取3个数字组成无重复数字的三位数，其中若有1和3时，3必须排在1的前面；若只有1和3中的一个时，它应排在其他数字的前面，这样不同的三位数共有________个(用数字作答)．【答案】60(二)正难则反思想【方法解读】在解决一些数学问题时，有时候会碰到正面解决非常复杂的情况，对于正面处理较复杂或不易求解的问题，常常从问题的对立面去思考． 设集合S＝{1,2,3,4,5,6,7,8,9}，集合A＝{a1，a2，a3}是S的子集，且a1，a2，a3满足a1＜a2＜a3，a3－a2≤6，那么满足条件的集合A的个数为 (　　)A．78 B．76C．83 D．84【答案】C【解析】若从正面考虑，需分当a3＝9时，a2可以取8,7,6,5,4,3，共6类；当a3＝8时，a2可以取7,6,5,4,3,2，共6类；分类较多，而其对立面a3－a2＞6包含的情况较少，当a3＝9时，a2取2，a1取1，只有这一种情况，利用正难则反思想解决．集合S的含有三个元素的子集的个数为C＝84.在这些含有三个元素的子集中能满足a1＜a2＜a3且a3－a2＞6的集合只有{1,2,9}，故满足题意的集合A的个数为84－1＝83.【点评】本题主要考查集合中元素的个数问题，考查组合的有关知识，解题时利用正难则反思想，回避较为复杂的分类讨论，可使问题简单化．2．由甲、乙、丙、丁4名学生参加数学、写作、英语三科竞赛，每科至少1人(且每人仅报一科)，若学生甲、乙不能同时参加同一竞赛，则不同的参赛方案共有________种．【答案】30(三)特殊化思想【方法解读】与二项式系数有关，包括求展开式中二项式系数最大的项、各项的二项式系数或系数的和、奇数项或者偶数项的二项式系数或系数的和以及各项系数的绝对值的和，主要方法是赋值法，通过特殊化思想求解，通过观察展开式右边的结构特点和所求式子的关系，确定给字母所赋的值，有时赋值后得到的式子比所求式子多一项或少一项，此时要专门求出这一项，而在求奇数项或者偶数项的二项式系数或系数的和时，往往要两次赋值，再由方程组求出结果． 若(x2－3x＋2)5＝a0＋a1x＋a2x2＋…＋a10x10.(1)求a2；(2)求a1＋a2＋…＋a10；(3)求(a0＋a2＋a4＋…＋a10)2－(a1＋a3＋…＋a7＋a9)2.(2)令x＝1，代入已知式可得a0＋a1＋a2＋…＋a10＝0，而令x＝0，得a0＝32，∴a1＋a2＋…＋a10＝－32.(3)令x＝－1可得(a0＋a2＋a4＋…＋a10)－(a1＋a3＋…＋a7＋a9)＝65，再由(a0＋a2＋a4＋…＋a10)＋(a1＋a3＋…＋a7＋a9)＝0，把这两个等式相乘可得，(a0＋a2＋a4＋…＋a10)2－(a1＋a3＋…＋a7＋a9)2＝65×0＝0.【点评】本题主要考查二项式展开式中系数的和问题，解决本题的关键是准确利用特殊法思想，通过赋值求解相应的系数的和．3．若(x2＋1)(x－3)9＝a0＋a1(x－2)＋a2(x－2)2＋a3(x－2)3＋…＋a11(x－2)11，则a1＋a2＋a3＋…＋a11的值为________．【答案】5【解析】令x＝2，得a0＝(22＋1)(2－3)9＝－5，令x＝3，得a0＋a1＋a2＋a3＋…＋a11＝(32＋1)(3－3)9＝0，所以a1＋a2＋a3＋…＋a11＝－a0＝5.| 链接高考 |排列与组合的综合应用1．(2021年全国乙卷)将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目中进行培训，每名志愿者只分配到1个项目中，每个项目至少分配1名志愿者，则不同的分配方案共有 (　　)A．60种 B．120种C．240种 D．480种【答案】C2．(2020年新课标卷Ⅱ)4名同学到3个小区参加垃圾分类宣传活动，每名同学只去1个小区，每个小区至少安排1名同学，则不同的安排方法共有________种．【答案】36二项式定理的应用【答案】C【答案】－46．(2021年浙江)已知多项式(x－1)3＋(x＋1)4＝x4＋a1x3＋a2x2＋a3x＋a4，则a1＝________，a2＋a3＋a4＝________.【答案】5　10【解析】由二项式定理，求得(x－1)3的展开式为(x－1)3＝x3－3x2＋3x－1，(x＋4)4的展开式为(x＋4)4＝x4＋4x3＋6x2＋4x＋1.所以a1＝1＋4＝5，a2＝－3＋6＝3，a3＝3＋4＝7，a4＝－1＋1＝0，所以a2＋a3＋a4＝10.