



四川省攀枝花市第七高级中学校2021-2022学年高二上学期第二次月考数学(理)试题
展开2023届高二上期第二次月考数学(理)试题
一. 选择题(本大题共小题,每小题分,总分分)
1. 椭圆x2+4y2=4的焦点坐标为( )
A. (±2,0) B. (0,±2) C. D.
2. 从装有除颜色外完全相同的个红球和个白球的口袋内任取个球,那么互斥而不对立的两个事件是( )
A. 至少有个白球;都是白球 B. 至少有个白球;至少有个红球
C. 恰有个白球;恰有个白球 D. 至少有个白球;都是红球
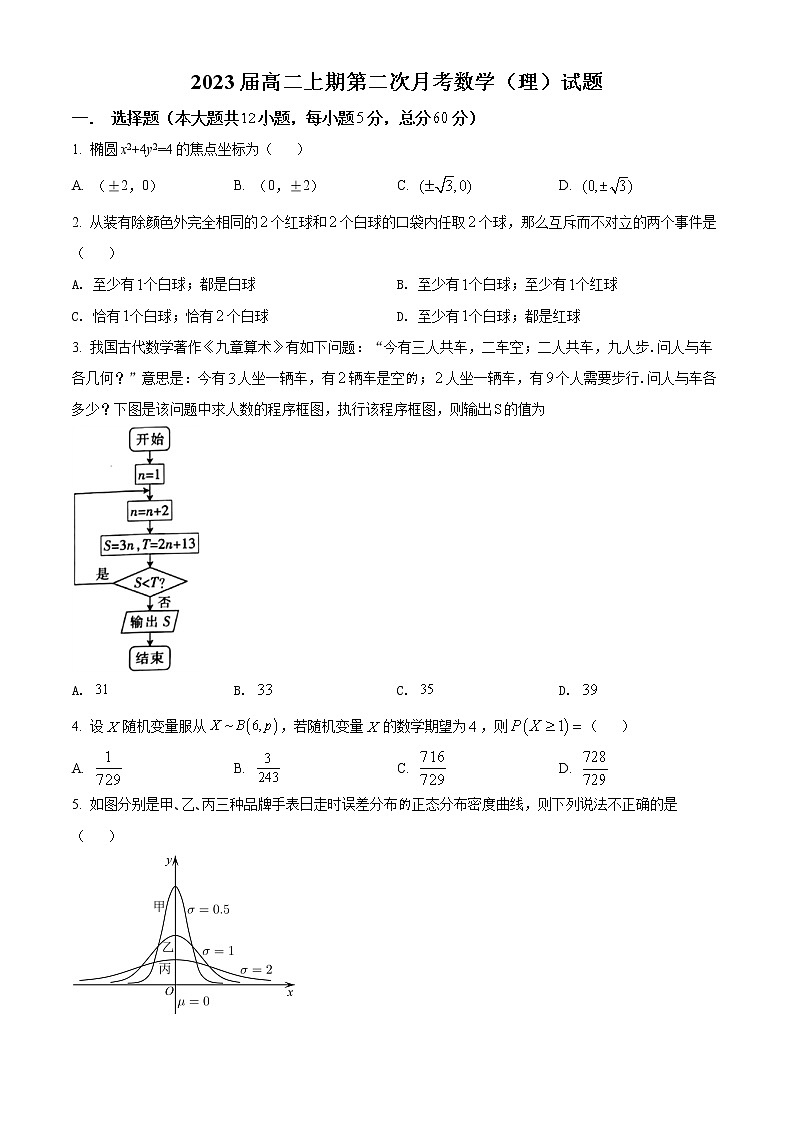
3. 我国古代数学著作《九章算术》有如下问题:“今有三人共车,二车空;二人共车,九人步.问人与车各几何?”意思是:今有人坐一辆车,有辆车是空;人坐一辆车,有个人需要步行.问人与车各多少?下图是该问题中求人数的程序框图,执行该程序框图,则输出的值为
A. B. C. D.
4. 设随机变量服从,若随机变量的数学期望为,则( )
A. B. C. D.
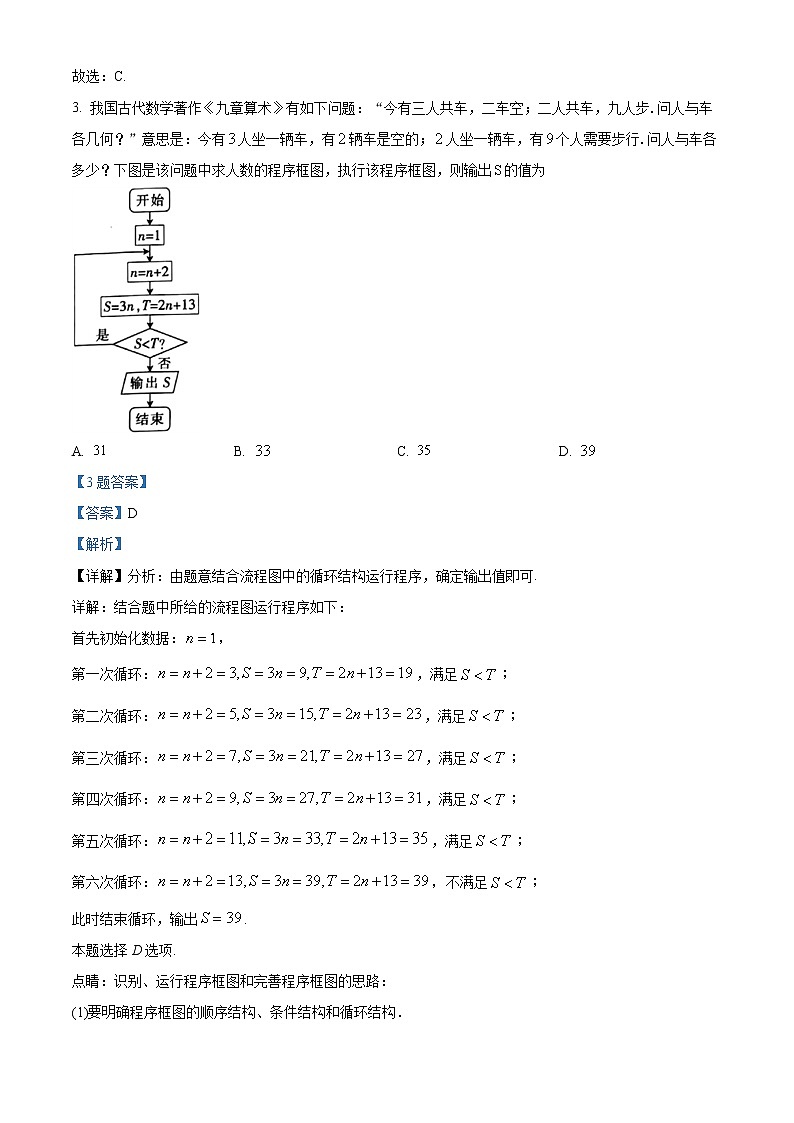
5. 如图分别是甲、乙、丙三种品牌手表日走时误差分布正态分布密度曲线,则下列说法不正确的是( )
A. 三种品牌的手表日走时误差的均值相等
B.
C. 三种品牌的手表日走时误差的方差从小到大依次为甲、乙、丙
D. 三种品牌手表中甲品牌的质量最好
6 五个同学排队,甲乙相邻且都不与丙相邻,则排队方式有几种( )
A. B. C. D.
7. 已知两定点,,直线:,在上满足的点的个数为( )
A. 0 B. 1 C. 2 D. 0或1或2
8. 在区间上任取两个数,则这两个数之和小于的概率是( )
A. B. C. D.
9. 若椭圆和双曲线的共同焦点为,,是两曲线的一个交点,则的值为 ( )
A. B. C. D.
10. 最近“你是什么垃圾?”这句流行语火爆全网,垃圾分类也成为时下热议的话题.银川市塞上骄子小区有如下六种垃圾桶:
一天,张三提着六袋分别属于不同垃圾桶的垃圾进行投放,发现每个垃圾箱再各投一袋垃圾就满了,作为一名法外狂徒,张三要随机投放垃圾,则法外狂徒张三恰好投错三袋垃圾的概率为( )
A. B. C. D.
11. 苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑,“门”的造型是东方之门的立意基础,“门”的内侧曲线呈抛物线型,如图1,两栋建筑第八层由一条长的连桥连接,在该抛物线两侧距连桥处各有一窗户,两窗户的水平距离为,如图2,则此抛物线顶端到连桥的距离为( )
A. B. C. D.
12. 已知F是双曲线﹣=1(a>0,b>0)的右焦点,A,B分别为其左、右顶点.O为坐标原点,D为其上一点,DF⊥x轴.过点A的直线l与线段DF交于点E,与y轴交于点M,直线BE与y轴交于点N,若3|OM|=2|ON|,则双曲线的离心率为( )
A. 3 B. 4 C. 5 D. 6
二. 填空题(本大题共小题,每小题分,总分分)
13. 某学校高一、高二、高三年级的学生人数之比为1:3:4,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为56的样本,则应从高二年级抽取________名学生.
14. 已知样本方差,则样本的方差为_______.
15. 某医院从3名医生和3名护士中选派4人参加志愿者服务,事件A表示选派的4人中至少有2名医生,事件B表示选派的4人中有2名护士,则___________.
16. 已知为双曲线:(,)的右焦点,为坐标原点,点是以为直径的圆与双曲线的一个公共点.若点关于点的对称点也在双曲线上,则双曲线的渐近线的斜率为___________.
三. 解答题(本大题共小题,总分分)
17. (1)已知中心在原点的双曲线的渐近线方程是,且双曲线过点,求双曲线的方程;
(2)已知椭圆的中心在坐标原点,右焦点的坐标为,直线交椭圆于两点,线段的中点为,求椭圆的方程;
18. 已知的展开式中所有项的二项式系数之和为1024.
(1)求展开式所有有理项(指数为整数);
(2)求的展开式中项的系数.
19. 某校从高三年级中选拔一个班级代表学校参加“学习强国知识大赛”,经过层层选拔,甲、乙两个班级进入最后决赛,规定回答1道相关问题做最后的评判选择由哪个班级代表学校参加大赛.每个班级4名选手,现从每个班级4名选手中随机抽取2人回答这个问题.已知这4人中,甲班级有3人可以正确回答这道题目,而乙班级4人中能正确回答这道题目的概率均为,甲、乙两班级每个人对问题的回答都是相互独立、互不影响的.
(1)求甲、乙两个班级抽取的4人都能正确回答的概率.
(2)设甲、乙两个班级被抽取的选手中能正确回答题目的人数分别为,,求随机变量,的期望,和方差,,并由此分析由哪个班级代表学校参加大赛更好.
21. 某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司在若干地区各投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益(单位:万元) | 2 | 3 | 3 |
| 7 |
由表中的数据显示,与之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出关于的回归直线方程.(参考公式:)
22. 已知,分别为椭圆()的左、右焦点,焦距为2,过作斜率存在且不为零的直线交于,两点,且的周长为8.
(1)求椭圆的方程;
(2)已知弦的垂直平分线交轴于点,求证:.
23. 已知抛物线的准线与直线的距离为4.
(1)求抛物线方程;
(2)、为抛物线上的两个不重合的动点,且线段的中点在直线上,设线段的垂直平分线为直线.
①证明:经过定点;
②若交轴于点,设的面积为,求的最大值.
本试卷的题干、答案和解析均由组卷网(http://zujuan.xkw.com)专业教师团队编校出品。
登录组卷网可对本试卷进行单题组卷、细目表分析、布置作业、举一反三等操作。
试卷地址:在组卷网浏览本卷
组卷网(http://zujuan.xkw.com)是学科网旗下智能题库,拥有小初高全学科超千万精品试题。
微信关注组卷网,了解更多组卷技能
学科网长期征集全国最新统考试卷、名校试卷、原创题,赢取丰厚稿酬,欢迎合作。
钱老师 QQ:537008204 曹老师 QQ:713000635
2023届四川省攀枝花市第七高级中学高三上学期第四次诊断考试数学(理)试题含解析: 这是一份2023届四川省攀枝花市第七高级中学高三上学期第四次诊断考试数学(理)试题含解析,共17页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
四川省攀枝花市第七高级中学校2021-2022学年高二上学期第二次月考数学(理)试题: 这是一份四川省攀枝花市第七高级中学校2021-2022学年高二上学期第二次月考数学(理)试题,共17页。试卷主要包含了 椭圆的焦点坐标为等内容,欢迎下载使用。
四川省攀枝花市第三高级中学校2021-2022学年高二上学期第三次月考数学(文)试题: 这是一份四川省攀枝花市第三高级中学校2021-2022学年高二上学期第三次月考数学(文)试题,共19页。试卷主要包含了 抛物线的焦点坐标为, 命题“,”的否定为, 已知等内容,欢迎下载使用。












