




高考数学(理数)二轮复习专题3 第1讲《立体几何的面积与体积》课件 (含详解)
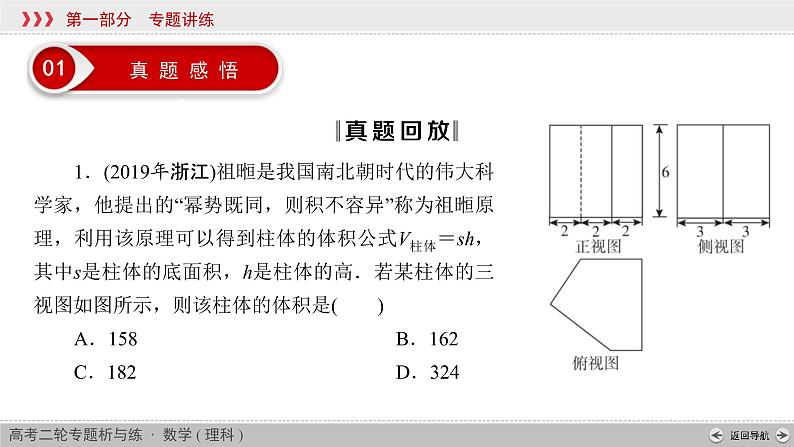
展开1.(2019年浙江)祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=sh,其中s是柱体的底面积,h是柱体的高.若某柱体的三视图如图所示,则该柱体的体积是( )A.158 B.162 C.182 D.324
4.(2019年新课标Ⅲ)学生到工厂劳动实践,利用3D打印技术制作模型,如图,该模型为长方体ABCD-A1B1C1D1,挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm,3D打印所用原料密度为0.9 g/cm3,不考虑打印损耗,制作该模型所需原料的质量为________g.【答案】118.8
1.空间几何体的表面积以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展开为平面图形计算,而表面积是侧面积与底面圆的面积之和.
2.空间几何体的体积三视图中的数据与原几何体中的数据不一定一一对应,识图要注意甄别.揭示空间几何体的结构特征,包括几何体的形状,平行垂直等结构特征,这些正是数据运算的依据.还原几何体的基本要素是“长对齐,高平直,宽相等”.简单几何体的三视图是该几何体在三个两两垂直的平面上的正投影,并不是从三个方向看到的该几何体的侧面表示的图形.在画三视图时,重叠的线只画一条,能看见的轮廓线和棱用实线表示,挡住的线要画成虚线.
求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解;若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.3.球体解决球与其他几何体的切、接问题,关键在于仔细观察、分析,弄清相关元素的位置关系和数量关系,选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系),达到空间问题平面化的目的.
例1 (2017年新课标Ⅰ)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个面是梯形,这些梯形的面积之和为( )A.10 B.12 C.14 D.16【答案】B
(2018年新课标Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )
例2 (2019年上海)一个直角三角形的两条直角边长分别为1和2,将该三角形分别绕其两条直角边旋转得到的两个圆锥的体积之比为( )A.1 B.2 C.4 D.8【分析】直角三角形绕直角边旋转得到圆锥,两条直角边分别为圆锥底面圆的半径与圆锥的高.【答案】B
求空间几何体体积的常用方法:(1)公式法:直接根据相关的体积公式计算.(2)等积法:根据体积计算公式,通过转换空间几何体的底面和高使得体积计算更容易,或是求出一些体积比等.(3)割补法:把不能直接计算体积的空间几何体进行适当的分割或补形,转化为可计算体积的几何体.
【分析】求球体的体积需先求半径,找到外接球的球心(到各顶点距离相等的点)即可.【答案】D
研究球的表面积和体积的时候要注意利用球的大圆,把空间图形转化为平面图形来研究,并且要熟练掌握垂径定理等平面几何中圆的性质.
高考数学(理数)二轮复习专题5 第3讲《数列的综合问题》课件 (含详解): 这是一份高考数学(理数)二轮复习专题5 第3讲《数列的综合问题》课件 (含详解),共38页。PPT课件主要包含了数列的实际应用,数列与其他知识的交汇,专题复习检测等内容,欢迎下载使用。
高考数学(理数)二轮复习专题1 第3讲《函数与方程》课件 (含详解): 这是一份高考数学(理数)二轮复习专题1 第3讲《函数与方程》课件 (含详解),共47页。PPT课件主要包含了函数图象,函数零点问题,利用导数证明不等式,专题复习检测等内容,欢迎下载使用。
高考数学(理数)二轮复习专题4 第3讲《算法初步与复数》课件 (含详解): 这是一份高考数学(理数)二轮复习专题4 第3讲《算法初步与复数》课件 (含详解),共39页。PPT课件主要包含了条件结构,循环结构,复数的有关概念,复数代数形式的运算,专题复习检测等内容,欢迎下载使用。












